計數排序雖然不是面試常考題目，但是計數排序的求統計數組步驟和最后元素歸位思想是我們刷題時經常用到的，例如原地置換，使用數組模擬 hashmap 等，所以還是很有必要看一下的。

今天我們就一起來看看線性排序里的計數排序到底是怎么回事吧。

我們將鏡頭切到袁記菜館

因為今年袁記菜館的效益不錯，所以袁廚就想給員工發些小福利，讓小二根據員工工齡進行排序，但是菜館共有 100000 名員工，菜館開業 10 年，員工工齡從 0 - 10 不等。

看來這真是一個艱巨的任務啊。

當然我們可以借助之前說過的 歸并排序 和 快速排序 解決，但是我們有沒有其他更好的方法呢？

了解排序算法的老哥可能已經猜到今天寫什么啦。是滴，我們今天來寫寫用空間換時間的線性排序。

說之前我們先來回顧一下之前的排序算法，最好的時間復雜度為 O（nlogn） ，且都基于元素之間的比較來進行排序。

我們來說一下非基于元素比較的排序算法，且時間復雜度為 O（n），時間復雜度是線性的，所以我們稱其為線性排序算法。

其優勢在于在對一定范圍內的整數排序時，它的復雜度為Ο（n+k），此時的 k 則代表整數的范圍。快于任何一種比較類排序算法，不過也是需要犧牲一些空間來換取時間。

下面我們先來看看什么是計數排序，這個計數的含義是什么？

我們假設某一分店共有 10 名員工，

工齡分別為 1，2，3，5，0，2，2，4，5，9

那么我們將其存在一個長度為 10 的數組里，，但是我們注意，我們數組此時存的并不是元素值，而是元素的個數。見下圖

注：此時我們這里統計次數的數組長度根據最大值來決定，上面的例子中最大值為 9 ，則長度為 9 + 1 = 10。暫且先這樣理解，后面會對其優化 。

我們繼續以上圖的例子來說明，在該數組中，索引代表的為元素值（也就是上面例子中的工齡），數組的值代表的則是元素個數（也就是不同工齡出現的次數）。

即工齡為 0 的員工有 1 個， 工齡為 1 的員工有 1 個，工齡為 2 的員工有 3 個 。。。

然后我們根據出現次數將其依次取出看看是什么效果。

0，1，2，2，2，3，4，5，5，9

我們發現此時元素則變成了有序的，但是這并不是排序，只是簡單的按照統計數組的下標，輸出了元素值，并沒有真正的給原始數組進行排序。

這樣操作之后我們不知道工齡屬于哪個員工。

見下圖

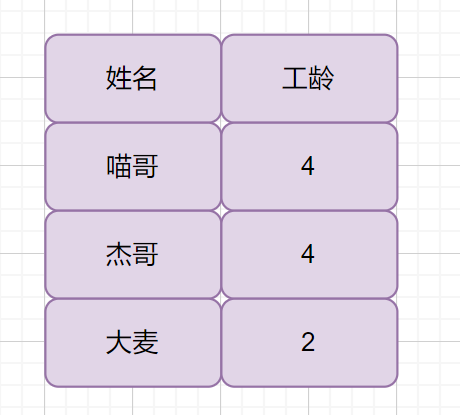
舉例

雖然喵哥和杰哥工齡相同，如果我們按照上面的操作輸出之后，我們不能知道工齡為 4 的兩個員工，哪個是喵哥哪個是杰哥。

所以我們需要借助其他方法來對元素進行排序。

大家還記不記得我們之前說過的前綴和，下面我們通過上面統計次數的數組求出其前綴和數組。

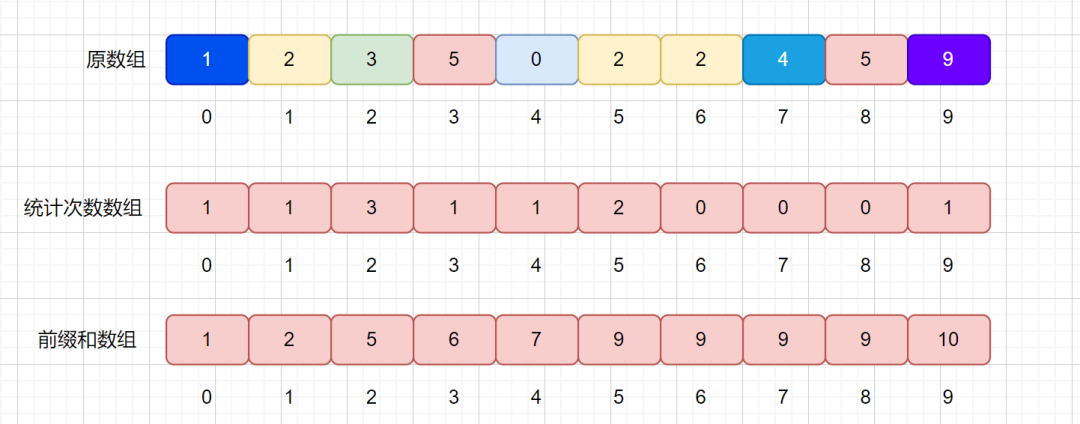
因為我們是通過統計次數的數組得到了前綴和數組，那么我們來分析一下 presum 數組里面值的含義。

例如我們的 presum［2］ = 5 ，代表的則是原數組小于等于 2 的值共有 5 個。presum［4］ = 7 代表小于等于 4 的元素共有 7 個。

是不是感覺計數排序的含義要慢慢顯現出來啦。

其實到這里我們已經可以理解的差不多了，還差最后一步，

此時我們要從后往前遍歷原始數組，然后將遍歷到的元素放到臨時數組的合適位置，并修改 presum 數組的值，遍歷結束后則達到了排序的目的。

這時有人要問了，為什么我們要從后往前遍歷呢？

這個問題的答案，我們等下說，繼續往下看吧。

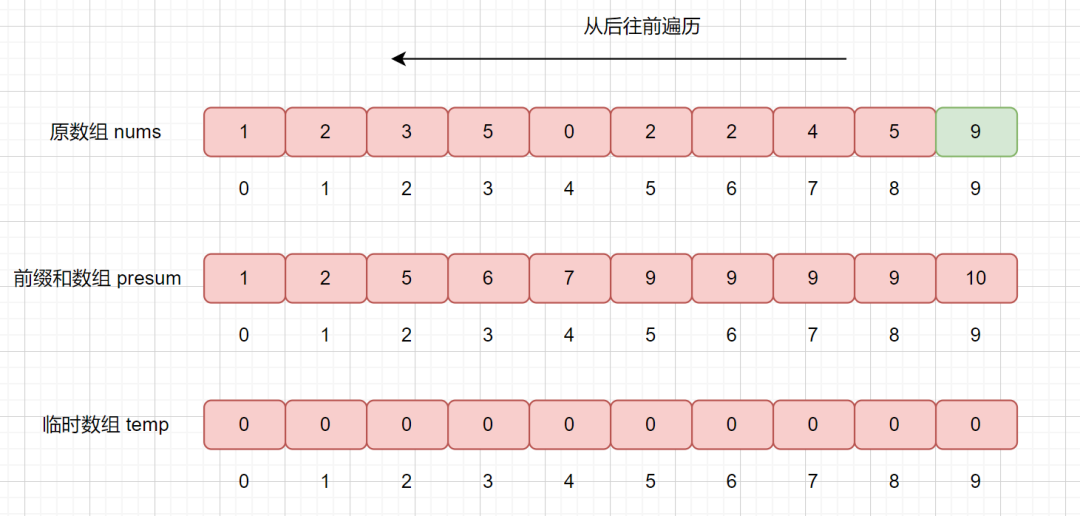
計數排序

我們從后往前遍歷，nums［9］ = 9，則我們拿該值去 presum 數組中查找，發現 presum［nums［9］］ = presum［9］ = 10 ，

大家還記得我們 presum 數組里面每個值的含義嗎，我們此時 presum［9］ = 10，則代表在數組中，小于等于的數共有 10 個，則我們要將他排在臨時數組的第 10 個位置，也就是 temp［9］ = 9。

我們還需要干什么呢？我們想一下，我們已經把 9 放入到 temp 數組里了，已經對其排好序了，那么我們的 presum 數組則不應該再統計他了，則將相應的位置減 1 即可，也就是 presum［9］ = 10 - 1 = 9;

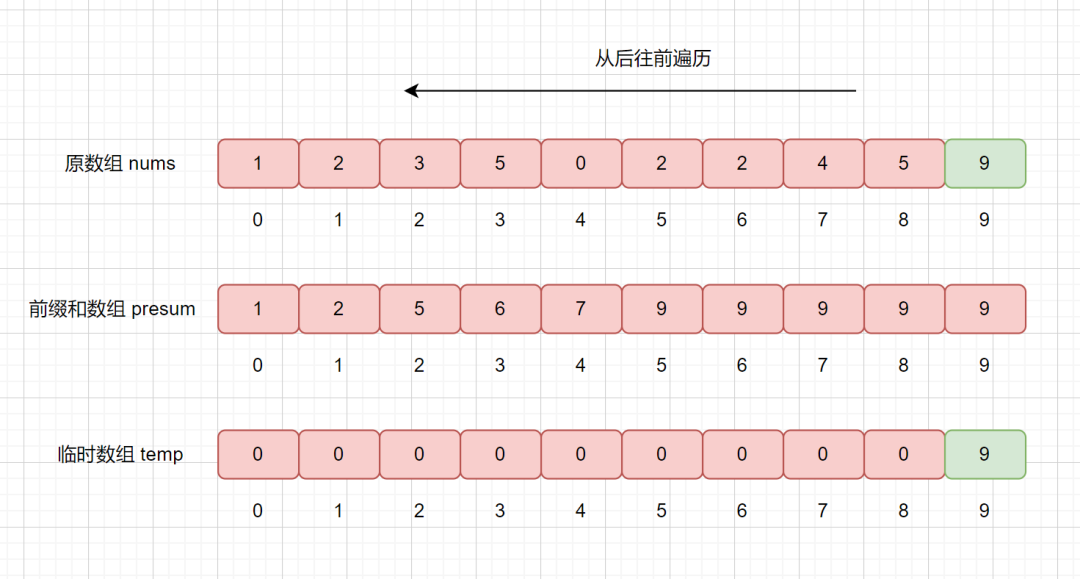
下面我們繼續遍歷 5 ，然后同樣執行上訴步驟

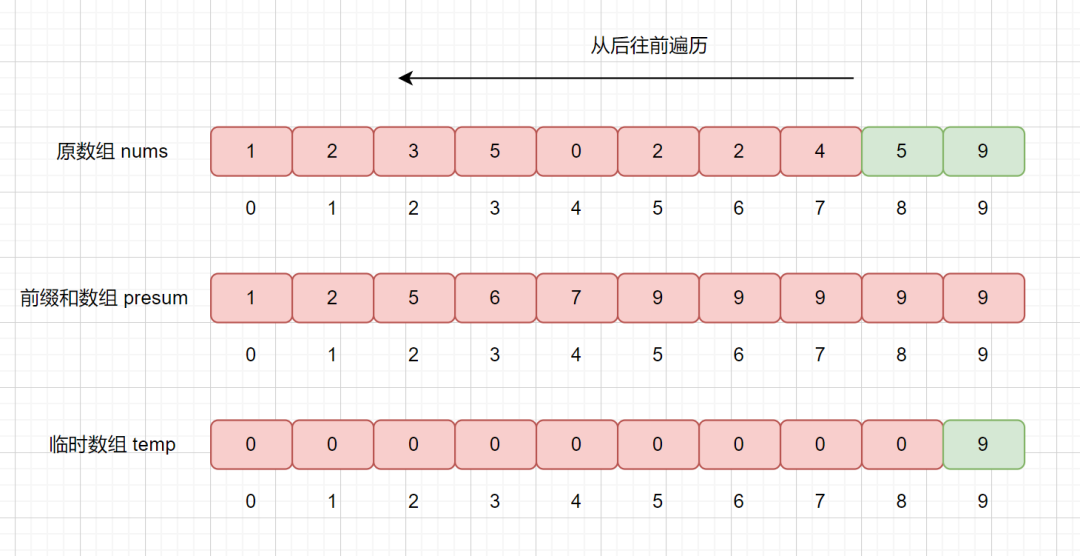
我們繼續查詢 presum 數組，發現 presum［5］ = 9，則說明小于等于 5 的數共有 9 個，我們將其放入到 temp 數組的第 9 個位置，也就是

temp［8］ = 5。然后再將 presum［5］ 減 1 。

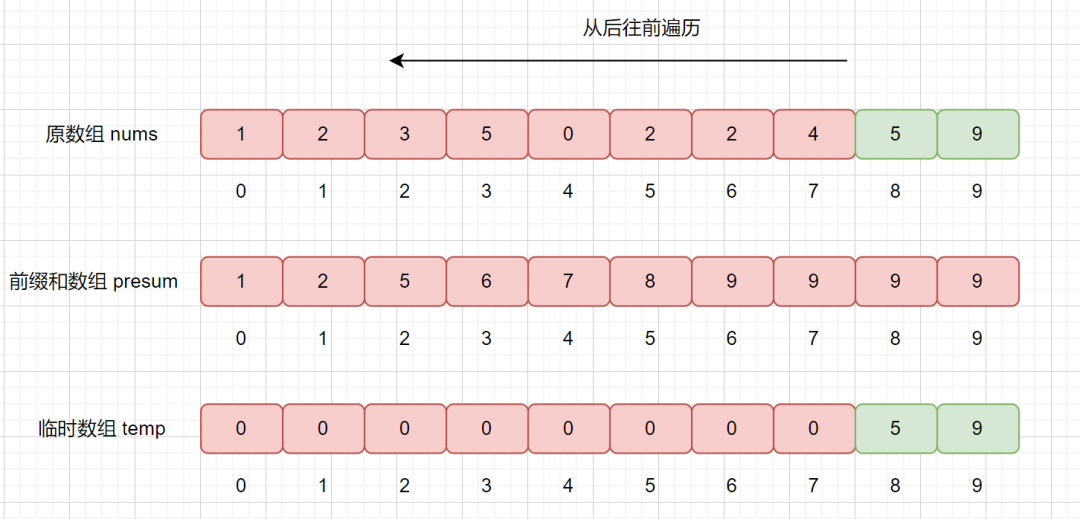
是不是到這里就理解了計數排序的大致思路啦。

那么我們為什么需要從后往前遍歷呢？我們思考一下，如果我們從前往后遍歷，相同元素的話，前面的元素則會先歸位再減一，這樣則會使計數排序變成不穩定的排序算法。

這個排序的過程像不像查字典呢？通過查詢 presum 數組，得出自己應該排在臨時數組的第幾位。然后再修改下字典，直到遍歷結束。

那么我們先來用動畫模擬一下我們這個 bug 版的計數排序，加深理解。

注：我們得到 presum 數組的過程在動畫中省略。直接模擬排序過程。

計數排序

但是到現在就完了嗎？顯然沒有，我們思考下這個情況。

假如我們的數字為 90，93，94，91，92 如果我們根據上面方法設置 presum 數組的長度，那我們則需要設置數組長度為 95（因為最大值是94），這樣顯然是不合理的，會浪費掉很多空間。

還有就是當我們需要對負數進行排序時同樣會出現問題，因為我們求次數的時候是根據 nums［index］ 的值來填充 presum 數組的，所以當 nums［index］ 為負數時，填充 presum 數組時則會報錯。

此時通過最大值來定義數組長度也不合理。

所以我們需要采取別的方法來定義數組長度。

下面我們來說一下偏移量的概念。

例如 90，93，94，91，92，我們 可以通過 max ，min 的值來設置數組長度即 94 - 90 + 1 = 5 。偏移量則為 min 值，也就是 90。那么我們的 90 則對應索引 0 。

見下圖。

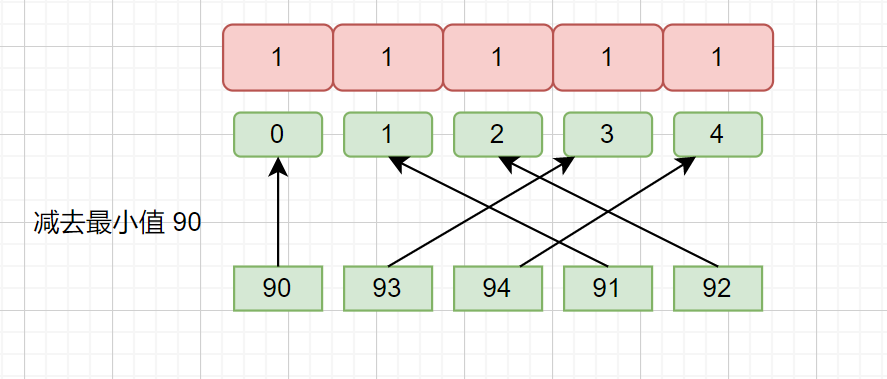
這樣我們填充 presum 數組時就不會出現浪費空間的情況了，負數？出現負數的情況當然也可以。繼續看

例如：-1，-3，0，2，1

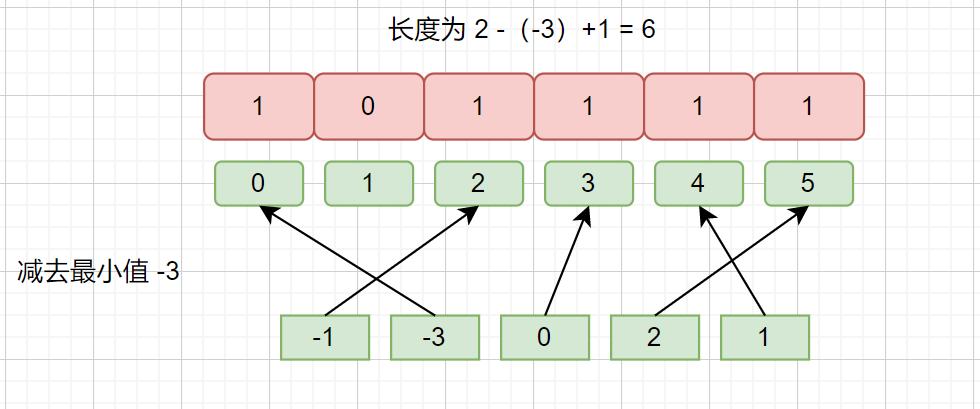
一樣可以，哦了，到這里我們就搞定了計數排序，下面我們來看一哈代碼吧。

class Solution {

public int［］ sortArray（int［］ nums） {

int len = nums.length;

if （nums.length 《 1） {

return nums;

}

//求出最大最小值

int max = nums［0］;

int min = nums［0］;

for （int x ： nums） {

if （max 《 x） max = x;

if （min 》 x） min = x;

}

//設置 presum 數組長度，然后求出我們的前綴和數組，

//這里我們可以把求次數數組和前綴和數組用一個數組處理

int［］ presum = new int［max-min+1］;

for （int x ： nums） {

presum［x-min］++;

}

for （int i = 1; i 《 presum.length; ++i） {

presum［i］ = presum［i-1］+presum［i］;

}

//臨時數組

int［］ temp = new int［len］;

//遍歷數組，開始排序，注意偏移量

for （int i = len-1; i 》= 0; --i） {

//查找 presum 字典，然后將其放到臨時數組，注意偏移度

int index = presum［nums［i］-min］-1;

temp［index］ = nums［i］;

//相應位置減一

presum［nums［i］-min］--;

}

//copy回原數組

System.arraycopy（temp，0，nums，0，len）;

return nums;

}

}

好啦，這個排序算法我們已經搞定了，下面我們來扒一扒它。

計數排序時間復雜度分析

我們的總體運算量為 n+n+k+n ，總體運算是 3n + k 所以時間復雜度為 O（N+K）；

計數排序空間復雜度分析

我們用到了輔助數組，空間復雜度為 O（n）

計數排序穩定性分析

穩定性在我們最后存入臨時數組時有體現，我們當時讓其放入臨時數組的合適位置，并減一，所以某元素前面的相同元素，在臨時數組，仍然在其前面。所以計數排序是穩定的排序算法。

雖然計數排序效率不錯但是用到的并不多。

這是因為其當數組元素的范圍太大時，并不適合計數排序，不僅浪費時間，效率還會大大降低。

當待排序的元素非整數時，也不適用，大家思考一下這是為什么呢？好啦，今天的文章就到這啦，我們下期再見，拜了個拜

巨人的肩膀

算法導論

極客時間數據結構與算法之美
編輯：lyn