在本篇文章中,我們會展開一個(gè)適用于采用相控陣前端的雷達(dá)和無線系統(tǒng)應(yīng)用的主題。 內(nèi)容涵蓋:
如何在相控陣設(shè)計(jì)中應(yīng)用優(yōu)化技術(shù)。
什么是二次規(guī)劃?
在設(shè)計(jì)過程中采用優(yōu)化解算器。
當(dāng)設(shè)計(jì)大型相控陣系統(tǒng)時(shí),這種優(yōu)化工作流程可以節(jié)省大量時(shí)間,因?yàn)榇诉^程會涉及很多設(shè)計(jì)參數(shù),包括單個(gè)天線單元的位置和應(yīng)用到每個(gè)天線單元的權(quán)重。因此,當(dāng)從事電磁解算器層級的物理陣列設(shè)計(jì)工作以及系統(tǒng)層級陣列設(shè)計(jì)工作時(shí),可以采用這些優(yōu)化技術(shù)。
本文專注于系統(tǒng)級應(yīng)用,同時(shí)我們在文章末尾提供了一個(gè)鏈接,通過其可以獲取有關(guān)電磁解算器級應(yīng)用的更多資源。
與單天線天線單元相比,相控陣的一個(gè)主要優(yōu)點(diǎn)是可以形成一個(gè)波束(或多個(gè)波束),以增強(qiáng)所需的信號并降低干擾信號的影響。
通常,在合成一種方向圖時(shí),N 天線單元相控陣可提供 N 個(gè)自由度。這意味著可以調(diào)整N個(gè)權(quán)值,每個(gè)天線單元一個(gè)權(quán)值,以控制波束形狀,從而滿足一些預(yù)定義的約束。
正如在這篇博客(https://www.mwrf.com/technologies/systems/article/21849359/algorithms-to-antenna-synthesizing-an-antenna-array-with-optimization-techniques)中所述,可以采用各種技術(shù)來實(shí)現(xiàn)方向圖合成,包括調(diào)零、加窗和稀布(Thinning)。應(yīng)用優(yōu)化技術(shù)有助于消除方向圖合成時(shí)的“反復(fù)試錯(cuò)”過程。
許多常用的波束形成技術(shù)都可以表示為優(yōu)化問題。例如,最小方差無失真響應(yīng)(MVDR)波束形成器用于最大限度減小總噪聲輸出,同時(shí)保留給定方向的信號。我們之前在另一篇博客中介紹了此類波束形成器,但在數(shù)學(xué)上,通過解決優(yōu)化問題即可得到MVDR波束形成權(quán)值。
在本文中,我們省略了數(shù)學(xué)運(yùn)算,但是一個(gè) N 天線單元陣列能夠處理 N?1 個(gè)約束。MVDR 波束形成器可以進(jìn)行擴(kuò)展,以包含更多約束,從而成為線性約束最小方差(LCMV)波束形成器。LCMV 波束形成器中的附加約束常用于消除給定方向的干擾。
這些技術(shù)適用于任何陣列結(jié)構(gòu),但我們考慮一個(gè)包含 32 個(gè)天線單元、天線單元之間具有半波長間距的均勻線性陣列。我們可以采用 LCMV 方法執(zhí)行陣列合成。我們的相關(guān)信號位于0度方位,干擾源位于 -70 度、-40 度和 -20 度方位。噪聲功率假定比信號低 40 dB。圖 1 顯示了我們的方向圖結(jié)果。此波束形成器可有效消除垂直虛線圖中所示方向的噪聲源。
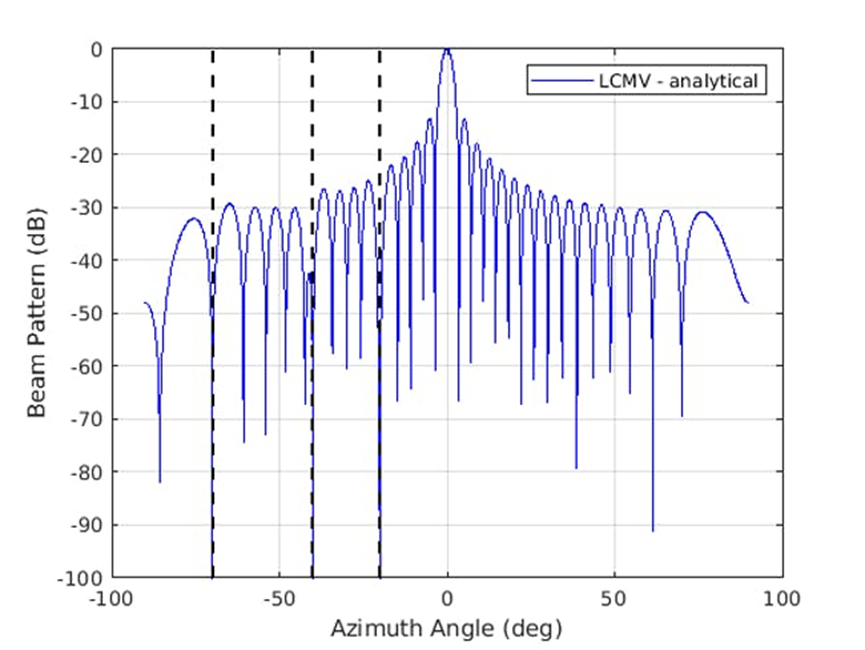
1.LCMV波束形成器用于消除干擾源。(2021 The MathWorks, Inc.)
MVDR 和 LCMV 算法的一個(gè)共同點(diǎn)是只處理等式約束。但是,方向圖合成的另一常見要求是確保陣列響應(yīng)一組給定的角度范圍內(nèi)低于某一閾值。例如,我們可以將以下要求添加到所需方向圖中:
1. 在 ?30 和 ?10 度方位之間,旁瓣應(yīng)低于 ?40 dB。
2. 在主瓣以外的任何地方,旁瓣應(yīng)低于 ?20 dB。
圖 2 闡述了我們將嘗試實(shí)現(xiàn)的系統(tǒng)所需的方向圖要求。
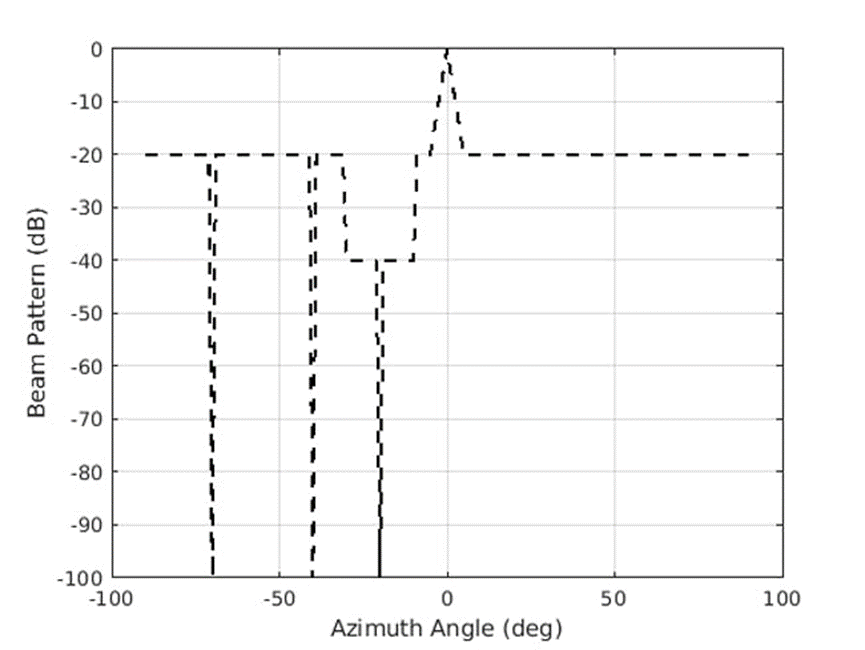
2.圖示為陣列方向圖的所需特性。(2021 The MathWorks, Inc.)
MVDR 和 LCMV 算法無法再用于解決此類問題,因此我們想介紹另一種涉及優(yōu)化解算器的技術(shù)。
優(yōu)化解算器用于最小化給定約束集下的目標(biāo)函數(shù)。基于目標(biāo)函數(shù)和約束條件,一些優(yōu)化解算器比其他解算器更有效。因此,選擇適合應(yīng)用的優(yōu)化解算器非常重要。
在本文中,由于目標(biāo)函數(shù)旨在最大限度減小功率,所以很自然地將其視為二次規(guī)劃(QP)問題。例如,可以使用優(yōu)化工具箱中(https://www.mathworks.com/products/optimization.html)的 quadprog 函數(shù)。
盡管 QP 解算器似乎很適合我們的方向圖合成問題,但是將陣列合成問題轉(zhuǎn)化為 QP 公式并不簡單。這是因?yàn)榻馑闫魍ǔL幚韺?shí)數(shù),而陣列方向圖計(jì)算會涉及復(fù)數(shù)。我們需要首先將復(fù)數(shù)運(yùn)算轉(zhuǎn)化為實(shí)數(shù)運(yùn)算,形成目標(biāo)函數(shù)和約束的實(shí)部和虛部,然后確立二次規(guī)劃并使用解算器。
圖 3 所示為使用合成權(quán)值產(chǎn)生的方向圖。請注意重疊的虛線部分,這就是我們的所需要求。?70、?40 和?20 度方位均為零,并實(shí)現(xiàn)了新的旁瓣水平。
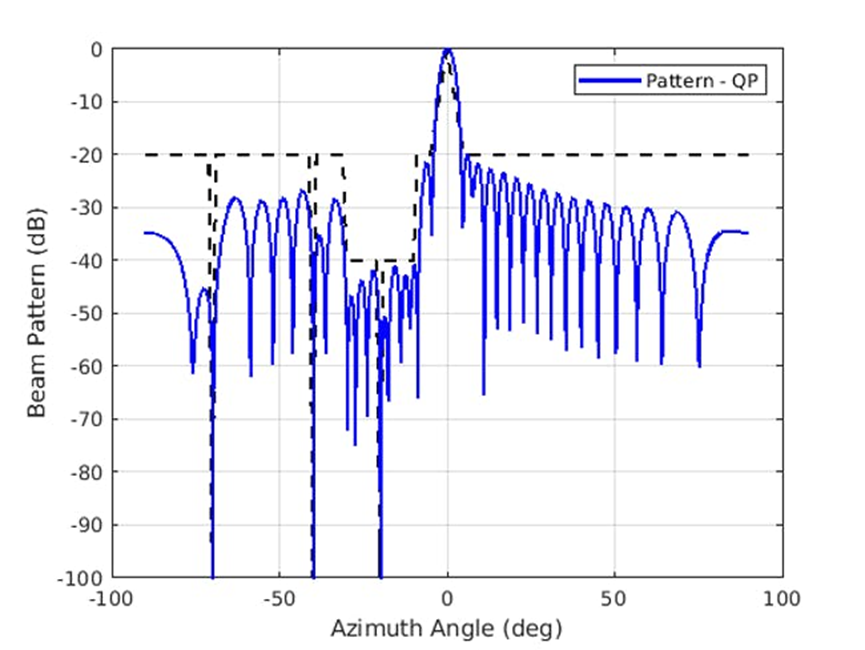
3.此合成方向圖采用二次規(guī)劃優(yōu)化技術(shù),滿足了所需要求。(2021 The MathWorks, Inc.)
二次規(guī)劃可以完成此項(xiàng)工作。但是,為了將復(fù)數(shù)約束轉(zhuǎn)化為實(shí)數(shù)約束,我們不得不分別考慮實(shí)部和虛部,而在理論上,我們只需要確保兩者的范數(shù)滿足不等式。因此,在QP公式中,我們對波束方向圖的實(shí)部和虛部采用更嚴(yán)格的約束。
另一種優(yōu)化解算器稱為二階錐規(guī)劃(SOCP),具有以范數(shù)形式定義的約束。此解算器可為解決我們的問題提供另一種可行的選擇。
此外,由于我們方向圖合成問題中的約束更自然地與 SOCP 公式相匹配,所以我們預(yù)計(jì)采用 SOCP 獲得的結(jié)果可能優(yōu)于通過QP獲得的結(jié)果。
但是,即使 SOCP 問題的目標(biāo)函數(shù)是線性函數(shù)而不是范數(shù),也可以將包含范數(shù)的原目標(biāo)函數(shù)轉(zhuǎn)化為附加的二階錐約束。然后,可以利用 SOCP 解決我們的最小方差方向圖合成問題。
圖 4 展示了采用優(yōu)化工具箱中的 coneprog 函數(shù)實(shí)現(xiàn)的方向圖。將此結(jié)果與通過 QP 得到的方向圖進(jìn)行比較,我們可以看到,SOCP 解算器達(dá)到了更低的旁瓣水平。
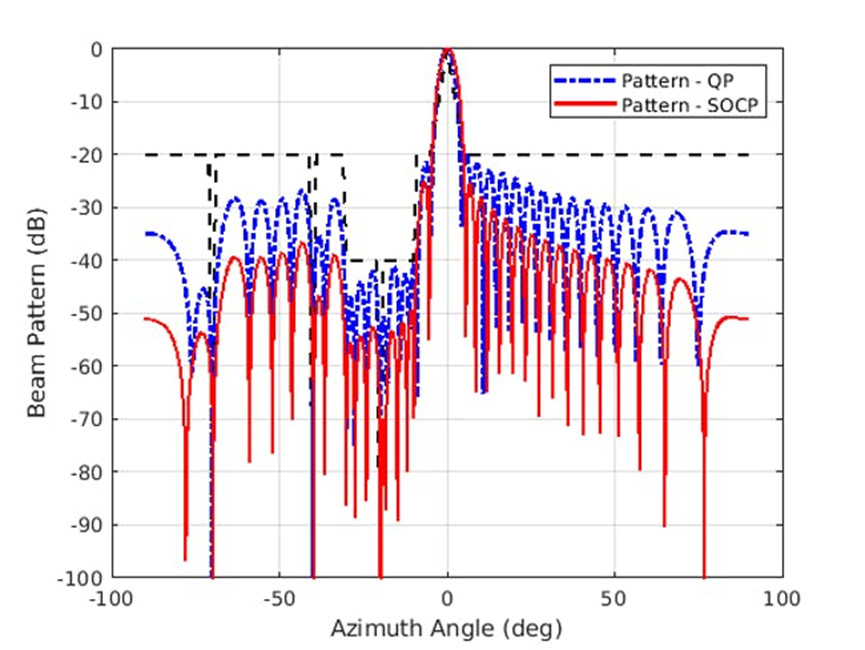
4.在這里,合成方向圖采用二次規(guī)劃優(yōu)化技術(shù),滿足了所需要求,并與SOCP相比。(2021 The MathWorks, Inc.)您可以采用相控陣系統(tǒng)工具箱、天線工具箱和優(yōu)化工具箱設(shè)計(jì)系統(tǒng)中的陣列。相控陣系統(tǒng)工具箱 https://www.mathworks.com/products/phased-array.html 天線工具箱 https://www.mathworks.com/products/antenna.html 優(yōu)化工具箱 https://www.mathworks.com/products/optimization.html
審核編輯 :李倩
-
天線
+關(guān)注
關(guān)注
70文章
3270瀏覽量
142023 -
相控陣
+關(guān)注
關(guān)注
3文章
93瀏覽量
14363 -
波束形成器
+關(guān)注
關(guān)注
0文章
8瀏覽量
8063
原文標(biāo)題:天線算法:相控陣合成優(yōu)化技術(shù)
文章出處:【微信號:MATLAB,微信公眾號:MATLAB】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
晶振對多功能相控陣雷達(dá)仿真系統(tǒng)的影響
深度解析如何利用時(shí)延解決方案最大化相控陣性能

嵌入式系統(tǒng)中的代碼優(yōu)化與壓縮技術(shù)
hyper v 顯卡,hyper-v顯卡:如何在虛擬機(jī)中配置和優(yōu)化顯卡性能
如何在電路中優(yōu)化GND連接 GND在高頻應(yīng)用中的挑戰(zhàn)
相控陣雷達(dá)電源芯片詳解
分析DCDC4644電源芯片在F-35戰(zhàn)機(jī)相控陣雷達(dá)的應(yīng)用
如何在電路設(shè)計(jì)中優(yōu)化電阻
DCDC 4644 電源芯片在相控陣雷達(dá)的應(yīng)用
如何在反激式拓?fù)?b class='flag-5'>中實(shí)現(xiàn)軟啟動






 如何在相控陣設(shè)計(jì)中應(yīng)用優(yōu)化技術(shù)
如何在相控陣設(shè)計(jì)中應(yīng)用優(yōu)化技術(shù)










評論