一、傅立葉變換的由來(lái)

關(guān)于傅立葉變換，無(wú)論是書(shū)本還是在網(wǎng)上可以很容易找到關(guān)于傅立葉變換的描述，但是大都是些故弄玄虛的文章，太過(guò)抽象，盡是一些讓人看了就望而生畏的公式的羅列，讓人很難能夠從感性上得到理解，最近，我偶爾從網(wǎng)上看到一個(gè)關(guān)于數(shù)字信號(hào)處理的電子書(shū)籍，是一個(gè)叫Steven W. Smith， Ph.D.外國(guó)人寫(xiě)的，寫(xiě)得非常淺顯，里面有七章由淺入深地專(zhuān)門(mén)講述關(guān)于離散信號(hào)的傅立葉變換。

雖然是英文文檔，我還是硬著頭皮看完了有關(guān)傅立葉變換的有關(guān)內(nèi)容，看了有茅塞頓開(kāi)的感覺(jué)，在此把我從中得到的理解拿出來(lái)跟大家分享。希望很多被傅立葉變換迷惑的朋友能夠得到一點(diǎn)啟發(fā)。

要理解傅立葉變換，確實(shí)需要一定的耐心，別一下子想著傅立葉變換是怎么變換的，當(dāng)然，也需要一定的高等數(shù)學(xué)基礎(chǔ)，最基本的是級(jí)數(shù)變換，其中傅立葉級(jí)數(shù)變換是傅立葉變換的基礎(chǔ)公式。

二、傅立葉變換的提出

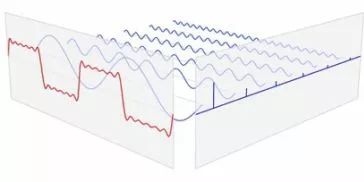
讓我們先看看為什么會(huì)有傅立葉變換？傅立葉是一位法國(guó)數(shù)學(xué)家和物理學(xué)家的名字，英語(yǔ)原名是Jean Baptiste Joseph Fourier（1768-1830），F(xiàn)ourier對(duì)熱傳遞很感興趣，于1807年在法國(guó)科學(xué)學(xué)會(huì)上發(fā)表了一篇論文，運(yùn)用正弦曲線(xiàn)來(lái)描述溫度分布，論文里有個(gè)在當(dāng)時(shí)具有爭(zhēng)議性的決斷：任何連續(xù)周期信號(hào)可以由一組適當(dāng)?shù)恼仪€(xiàn)組合而成。當(dāng)時(shí)審查這個(gè)論文的人，其中有兩位是歷史上著名的數(shù)學(xué)家拉格朗日（Joseph Louis Lagrange， 1736-1813） 和拉普拉斯 （Pierre Simon de Laplace，1749-1827），當(dāng)拉普拉斯和其它審查者投票通過(guò)并要發(fā)表這個(gè)論文時(shí)，拉格朗日?qǐng)?jiān)決反對(duì)，在近50年的時(shí)間里，拉格朗日?qǐng)?jiān)持認(rèn)為傅立葉的方法無(wú)法表示帶有棱角的信號(hào)，如在方波中出現(xiàn)非連續(xù)變化斜率。法國(guó)科學(xué)學(xué)會(huì)屈服于拉格朗日的威望，拒絕了傅立葉的工作，幸運(yùn)的是，傅立葉還有其它事情可忙，他參加了政治運(yùn)動(dòng)，隨拿破侖遠(yuǎn)征埃及，法國(guó)大革命后因會(huì)被推上斷頭臺(tái)而一直在逃避。直到拉格朗日死后15年，這個(gè)論文才被發(fā)表出來(lái)。

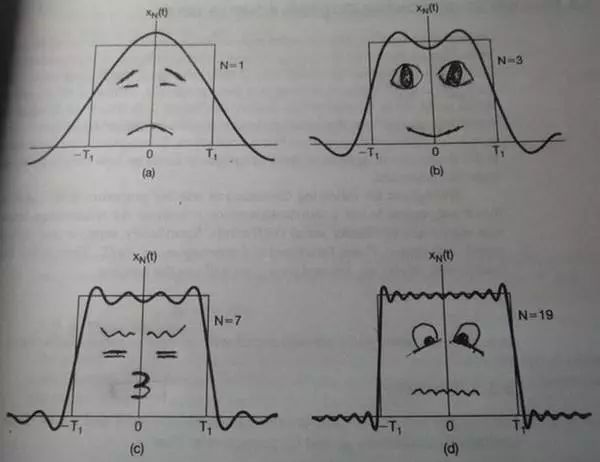
誰(shuí)是對(duì)的呢？拉格朗日是對(duì)的：正弦曲線(xiàn)無(wú)法組合成一個(gè)帶有棱角的信號(hào)。但是，我們可以用正弦曲線(xiàn)來(lái)非常逼近地表示它，逼近到兩種表示方法不存在能量差別，基于此，傅立葉是對(duì)的。

為什么我們要用正弦曲線(xiàn)來(lái)代替原來(lái)的曲線(xiàn)呢？如我們也還可以用方波或三角波來(lái)代替呀，分解信號(hào)的方法是無(wú)窮的，但分解信號(hào)的目的是為了更加簡(jiǎn)單地處理原來(lái)的信號(hào)。用正余弦來(lái)表示原信號(hào)會(huì)更加簡(jiǎn)單，因?yàn)檎嘞覔碛性盘?hào)所不具有的性質(zhì)：正弦曲線(xiàn)保真度。一個(gè)正弦曲線(xiàn)信號(hào)輸入后，輸出的仍是正弦曲線(xiàn)，只有幅度和相位可能發(fā)生變化，但是頻率和波的形狀仍是一樣的。且只有正弦曲線(xiàn)才擁有這樣的性質(zhì)，正因如此我們才不用方波或三角波來(lái)表示。

三、傅立葉變換分類(lèi)

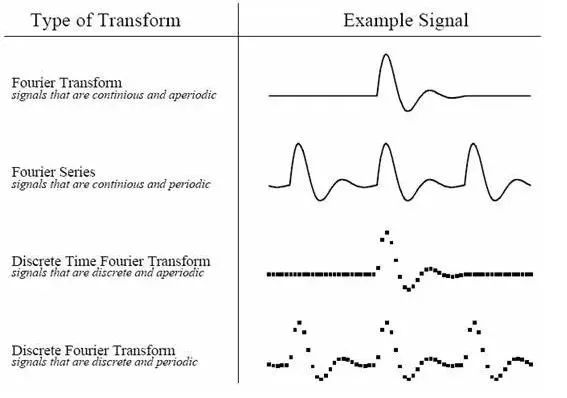
根據(jù)原信號(hào)的不同類(lèi)型，我們可以把傅立葉變換分為四種類(lèi)別：

非周期性連續(xù)信號(hào)：傅立葉變換 （Fourier Transform）

周期性連續(xù)信號(hào)：傅立葉級(jí)數(shù) （Fourier Series）

非周期性離散信號(hào)：離散時(shí)域傅立葉變換 （Discrete Time Fourier Transform）

周期性離散信號(hào)：離散傅立葉變換 （Discrete Fourier Transform）

下圖是四種原信號(hào)圖例：

這四種傅立葉變換都是針對(duì)正無(wú)窮大和負(fù)無(wú)窮大的信號(hào)，即信號(hào)的的長(zhǎng)度是無(wú)窮大的，我們知道這對(duì)于計(jì)算機(jī)處理來(lái)說(shuō)是不可能的，那么有沒(méi)有針對(duì)長(zhǎng)度有限的傅立葉變換呢？沒(méi)有。

因?yàn)檎嘞也ū欢x成從負(fù)無(wú)窮小到正無(wú)窮大，我們無(wú)法把一個(gè)長(zhǎng)度無(wú)限的信號(hào)組合成長(zhǎng)度有限的信號(hào)。面對(duì)這種困難，方法是把長(zhǎng)度有限的信號(hào)表示成長(zhǎng)度無(wú)限的信號(hào)，可以把信號(hào)無(wú)限地從左右進(jìn)行延伸，延伸的部分用零來(lái)表示，這樣，這個(gè)信號(hào)就可以被看成是非周期性離解信號(hào)，我們就可以用到離散時(shí)域傅立葉變換的方法。

還有，也可以把信號(hào)用復(fù)制的方法進(jìn)行延伸，這樣信號(hào)就變成了周期性離散信號(hào)，這時(shí)我們就可以用離散傅立葉變換方法進(jìn)行變換。這里我們要學(xué)的是離散信號(hào)，對(duì)于連續(xù)信號(hào)我們不作討論，因?yàn)橛?jì)算機(jī)只能處理離散的數(shù)值信號(hào)，我們的最終目的是運(yùn)用計(jì)算機(jī)來(lái)處理信號(hào)的。

但是對(duì)于非周期性的信號(hào)，我們需要用無(wú)窮多不同頻率的正弦曲線(xiàn)來(lái)表示，這對(duì)于計(jì)算機(jī)來(lái)說(shuō)是不可能實(shí)現(xiàn)的。所以對(duì)于離散信號(hào)的變換只有離散傅立葉變換 （DFT） 才能被適用，對(duì)于計(jì)算機(jī)來(lái)說(shuō)只有離散的和有限長(zhǎng)度的數(shù)據(jù)才能被處理，對(duì)于其它的變換類(lèi)型只有在數(shù)學(xué)演算中才能用到，在計(jì)算機(jī)面前我們只能用DFT方法，后面我們要理解的也正是DFT方法。這里要理解的是我們使用周期性的信號(hào)目的是為了能夠用數(shù)學(xué)方法來(lái)解決問(wèn)題，至于考慮周期性信號(hào)是從哪里得到或怎樣得到是無(wú)意義的。

每種傅立葉變換都分成實(shí)數(shù)和復(fù)數(shù)兩種方法，對(duì)于實(shí)數(shù)方法是最好理解的，但是復(fù)數(shù)方法就相對(duì)復(fù)雜許多了，需要懂得有關(guān)復(fù)數(shù)的理論知識(shí)，不過(guò)，如果理解了實(shí)數(shù)離散傅立葉變換 （real DFT），再去理解復(fù)數(shù)傅立葉就更容易了，所以我們先把復(fù)數(shù)的傅立葉放到一邊去，先來(lái)理解實(shí)數(shù)傅立葉變換，在后面我們會(huì)先講講關(guān)于復(fù)數(shù)的基本理論，然后在理解了實(shí)數(shù)傅立葉變換的基礎(chǔ)上再來(lái)理解復(fù)數(shù)傅立葉變換。

還有，這里我們所要說(shuō)的變換 （transform） 雖然是數(shù)學(xué)意義上的變換，但跟函數(shù)變換是不同的，函數(shù)變換是符合一一映射準(zhǔn)則的，對(duì)于離散數(shù)字信號(hào)處理 （DSP），有許多的變換：傅立葉變換、拉普拉斯變換、Z變換、希爾伯特變換、離散余弦變換等，這些都擴(kuò)展了函數(shù)變換的定義，允許輸入和輸出有多種的值，簡(jiǎn)單地說(shuō)變換就是把一堆的數(shù)據(jù)變成另一堆的數(shù)據(jù)的方法。

四、傅立葉變換的物理意義

傅立葉變換是數(shù)字信號(hào)處理領(lǐng)域一種很重要的算法。要知道傅立葉變換算法的意義，首先要了解傅立葉原理的意義。傅立葉原理表明：任何連續(xù)測(cè)量的時(shí)序或信號(hào)，都可以表示為不同頻率的正弦波信號(hào)的無(wú)限疊加。而根據(jù)該原理創(chuàng)立的傅立葉變換算法利用直接測(cè)量到的原始信號(hào)，以累加方式來(lái)計(jì)算該信號(hào)中不同正弦波信號(hào)的頻率、振幅和相位。

和傅立葉變換算法對(duì)應(yīng)的是反傅立葉變換算法。該反變換從本質(zhì)上說(shuō)也是一種累加處理，這樣就可以將單獨(dú)改變的正弦波信號(hào)轉(zhuǎn)換成一個(gè)信號(hào)。因此，可以說(shuō)，傅立葉變換將原來(lái)難以處理的時(shí)域信號(hào)轉(zhuǎn)換成了易于分析的頻域信號(hào)（信號(hào)的頻譜），可以利用一些工具對(duì)這些頻域信號(hào)進(jìn)行處理、加工。最后還可以利用傅立葉反變換將這些頻域信號(hào)轉(zhuǎn)換成時(shí)域信號(hào)。

從現(xiàn)代數(shù)學(xué)的眼光來(lái)看，傅里葉變換是一種特殊的積分變換。它能將滿(mǎn)足一定條件的某個(gè)函數(shù)表示成正弦基函數(shù)的線(xiàn)性組合或者積分。在不同的研究領(lǐng)域，傅里葉變換具有多種不同的變體形式，如連續(xù)傅里葉變換和離散傅里葉變換。

在數(shù)學(xué)領(lǐng)域，盡管最初傅立葉分析是作為熱過(guò)程的解析分析的工具，但是其思想方法仍然具有典型的還原論和分析主義的特征。“任意”的函數(shù)通過(guò)一定的分解，都能夠表示為正弦函數(shù)的線(xiàn)性組合的形式，而正弦函數(shù)在物理上是被充分研究而相對(duì)簡(jiǎn)單的函數(shù)類(lèi)：

傅立葉變換是線(xiàn)性算子，若賦予適當(dāng)?shù)姆稊?shù)，它還是酉算子；

傅立葉變換的逆變換容易求出，而且形式與正變換非常類(lèi)似；

正弦基函數(shù)是微分運(yùn)算的本征函數(shù)，從而使得線(xiàn)性微分方程的求解可以轉(zhuǎn)化為常系數(shù)的代數(shù)方程的求解。在線(xiàn)性時(shí)不變的卷積運(yùn)算為簡(jiǎn)單的乘積運(yùn)算，從而提供了計(jì)算卷積的一種簡(jiǎn)單手段；

離散形式的傅立葉的物理系統(tǒng)內(nèi)，頻率是個(gè)不變的性質(zhì)，從而系統(tǒng)對(duì)于復(fù)雜激勵(lì)的響應(yīng)可以通過(guò)組合其對(duì)不同頻率正弦信號(hào)的響應(yīng)來(lái)獲取；

著名的卷積定理指出：傅立葉變換可以化復(fù)變換可以利用數(shù)字計(jì)算機(jī)快速的算出（其算法稱(chēng)為快速傅立葉變換算法 （FFT））。

正是由于上述的良好性質(zhì)，傅里葉變換在物理學(xué)、數(shù)論、組合數(shù)學(xué)、信號(hào)處理、概率、統(tǒng)計(jì)、密碼學(xué)、聲學(xué)、光學(xué)等領(lǐng)域都有著廣泛的應(yīng)用。

五、圖像傅立葉變換的物理意義

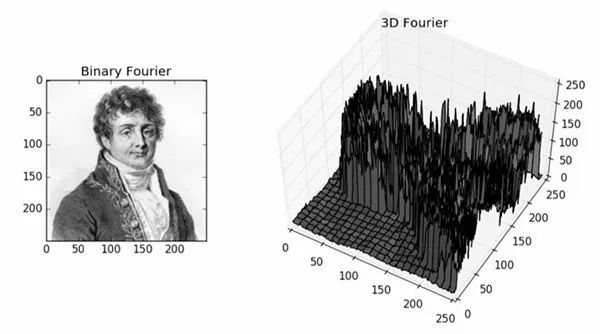
圖像的頻率是表征圖像中灰度變化劇烈程度的指標(biāo)，是灰度在平面空間上的梯度。如：大面積的沙漠在圖像中是一片灰度變化緩慢的區(qū)域，對(duì)應(yīng)的頻率值很低；而對(duì)于地表屬性變換劇烈的邊緣區(qū)域在圖像中是一片灰度變化劇烈的區(qū)域，對(duì)應(yīng)的頻率值較高。傅立葉變換在實(shí)際中有非常明顯的物理意義，設(shè)f是一個(gè)能量有限的模擬信號(hào)，則其傅立葉變換就表示f的譜。

從純粹的數(shù)學(xué)意義上看，傅立葉變換是將一個(gè)函數(shù)轉(zhuǎn)換為一系列周期函數(shù)來(lái)處理的。從物理效果看，傅立葉變換是將圖像從空間域轉(zhuǎn)換到頻率域，其逆變換是將圖像從頻率域轉(zhuǎn)換到空間域。換句話(huà)說(shuō)，傅立葉變換的物理意義是將圖像的灰度分布函數(shù)變換為圖像的頻率分布函數(shù)，傅立葉逆變換是將圖像的頻率分布函數(shù)變換為灰度分布函數(shù)。

傅立葉變換以前，圖像（未壓縮的位圖）是由對(duì)在連續(xù)空間（現(xiàn)實(shí)空間）上的采樣得到一系列點(diǎn)的集合，我們習(xí)慣用一個(gè)二維矩陣表示空間上各點(diǎn)，則圖像可由z=f（x，y）來(lái)表示。由于空間是三維的，圖像是二維的，因此空間中物體在另一個(gè)維度上的關(guān)系就由梯度來(lái)表示，這樣我們可以通過(guò)觀(guān)察圖像得知物體在三維空間中的對(duì)應(yīng)關(guān)系。

為什么要提梯度？因?yàn)閷?shí)際上對(duì)圖像進(jìn)行二維傅立葉變換得到頻譜圖，就是圖像梯度的分布圖，當(dāng)然頻譜圖上的各點(diǎn)與圖像上各點(diǎn)并不存在一一對(duì)應(yīng)的關(guān)系，即使在不移頻的情況下也是沒(méi)有。傅立葉頻譜圖上我們看到的明暗不一的亮點(diǎn)，實(shí)際上圖像上某一點(diǎn)與鄰域點(diǎn)差異的強(qiáng)弱，即梯度的大小，也即該點(diǎn)的頻率的大小（可以這么理解，圖像中的低頻部分指低梯度的點(diǎn)，高頻部分相反）。

一般來(lái)講，梯度大則該點(diǎn)的亮度強(qiáng)，否則該點(diǎn)亮度弱。這樣通過(guò)觀(guān)察傅立葉變換后的頻譜圖，也叫功率圖，我們首先就可以看出，圖像的能量分布，如果頻譜圖中暗的點(diǎn)數(shù)更多，那么實(shí)際圖像是比較柔和的（因?yàn)楦鼽c(diǎn)與鄰域差異都不大，梯度相對(duì)較小），反之，如果頻譜圖中亮的點(diǎn)數(shù)多，那么實(shí)際圖像一定是尖銳的，邊界分明且邊界兩邊像素差異較大的。

對(duì)頻譜移頻到原點(diǎn)以后，可以看出圖像的頻率分布是以原點(diǎn)為圓心，對(duì)稱(chēng)分布的。將頻譜移頻到圓心除了可以清晰地看出圖像頻率分布以外，還有一個(gè)好處，它可以分離出有周期性規(guī)律的干擾信號(hào)，比如正弦干擾，一副帶有正弦干擾，移頻到原點(diǎn)的頻譜圖上可以看出除了中心以外還存在以某一點(diǎn)為中心，對(duì)稱(chēng)分布的亮點(diǎn)集合，這個(gè)集合就是干擾噪音產(chǎn)生的，這時(shí)可以很直觀(guān)的通過(guò)在該位置放置帶阻濾波器消除干擾。

另外我還想說(shuō)明以下幾點(diǎn)：

圖像經(jīng)過(guò)二維傅立葉變換后，其變換系數(shù)矩陣表明：若變換矩陣Fn原點(diǎn)設(shè)在中心，其頻譜能量集中分布在變換系數(shù)短陣的中心附近。若所用的二維傅立葉變換矩陣Fn 的原點(diǎn)設(shè)在左上角，那么圖像信號(hào)能量將集中在系數(shù)矩陣的四個(gè)角上。這是由二維傅立葉變換本身性質(zhì)決定的。同時(shí)也表明一股圖像能量集中低頻區(qū)域。

變換之后的圖像在原點(diǎn)平移之前四角是低頻，最亮，平移之后中間部分是低頻，最亮，亮度大說(shuō)明低頻的能量大（幅角比較大）。

審核編輯 ：李倩