摘要:乘法是數字信號處理中重要的基本運算,在很大程度上影響著系統的性能。本文將介紹三種高速乘法器實現原理:陣列乘法器、華萊士(WT)乘法器、布斯華萊士樹超前進位乘法器。而且通過FPGA技術實現了這三種乘法器,并對基于以上三種架構的乘法器性能進行了分析比較。
關鍵字:陣列乘法器,華萊士乘法器,超前進位乘法器,FPGA
引言
隨著3G技術的發展,關于圖像、語音、加密等數字信號處理技術隨處可見,而且信號處理的實時性也要求越高。實時性即是要求對信號處理的速度要快,而乘法器是數字信號處理中重要的基本運算,在很大程度上影響著系統的性能。人們開始開發高速的乘法器。
以下將對三種乘法器:陣列乘法器、華萊士(WT)乘法器、布斯華萊士樹超前進位乘法器進行原理分析,并用FPGA技術實現了這三種乘法器,對其結果進行了仿真,得出相應的性能比較。
陣列乘法器
2.1 陣列乘法器原理
硬件乘法器的常規設計是適用“串行移位”和“并行加法”相結合的方法,這種方法并不需要很多器件。然而串行方法畢竟太慢,執行一次乘法的時間至少是執行一次加法時間的n倍,不能滿足科學技術對高速乘法所提出的要求。自從大規模集成電路問世以來,高速的單元陣列乘法器應運而生,出現了各種形式的流水線陣列乘法器,它們屬于并行乘法器,提供了極快的速度。陣列乘法器的運算過程如下:
第一:當乘數的位數字為1 時,我們可以將被乘數的值直接放置適當的位置。而適當的位置是依乘數的第幾個位和被乘數做運算之后所放的位置。
第二:當乘數的位數字為0 時,我們可以將0 放置適當的位置, 以作為部分乘積。
第三:我們利用筆和紙計算的乘法,在硬件中使用與門來實現。例如:1000 ×1中,乘數1 和每一個被乘數的位都個別做與運算,其結果為1000 正是我們所要的結果。由此可知我們只需用與門就可以完成我們所要的乘法。
第四:當部分乘積都運算完成后,使用加法來完成最終的乘法結果運算。
根據以上四點的說明,我們可以運用最簡單、最直觀的方式來描述固定點乘法器的電路描述。我們使用與門來做部分積運算,使用全加器(Full adder)來運算部分積的最終結果。圖1所示為有符號位的6×6固定點乘法器的架構圖。
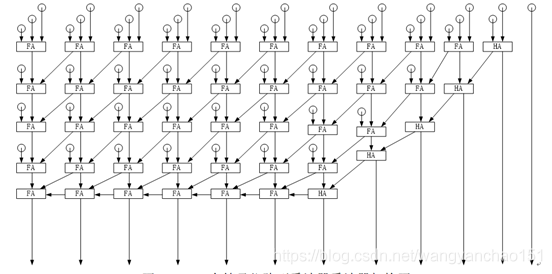
圖1 6×6有符號位陣列乘法器乘法器架構圖
2.2 陣列乘法器FPGA仿真
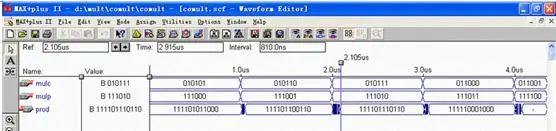
在名為comult的實體中設置mulc和mulp兩個輸入端口和一個prod輸出端口。其中mulc代表被乘數,mulp為乘數,二者均為6位。乘積prod是一個12位的結果,輸入與輸出端口的數據類型均為std_logic_vector。流程圖如圖2所示,仿真如圖3所示。
圖2 6x6有符號陣列乘法器流程圖
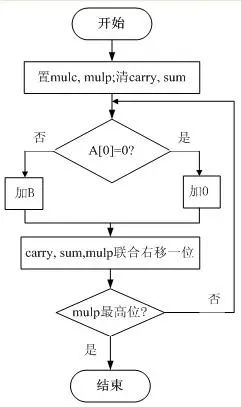
圖3 6x6有符號陣列乘法器仿真
華萊士乘法器原理
部分積相加, 若采用累加移位的方法, 速度太慢。華萊士樹算法(Wallace Tree Algorithm)是部分積化簡的一種樹形算法。它使乘法器的延時得到最大限度的縮短,但全加陣列的布局布線復雜度大為增加。
一個全加器有三個輸入: A , B , C (進位) 和兩個輸出S , C′(輸出進位) , 3個輸入對2個輸出而言是對稱的, 即它們互相交換位置, 結果不會受影響。如果把一串全加器簡單排成一行, 它們之間進位線不連, 把這樣一串全加器稱為保留進位加法器(CSA ) , 它有以下特性: 三個輸入數之和等于二個輸出數之和, 即3個相加數每通過一次保留進位加法器, 其個數就減少1個。
Wallace最早提出的方案就利用了這一特點:第一步將每列的部分積按三位進行分組,每組通過使用全加器構成的CSA部件,將加數的數目減少;第二步對第一步產生的結果仍按三位分組的方式將同權的偽和與局部進位信號通過CSA 部件進行處理,再次減少加數的數目,這種處理一直進行到最后只有兩個輸出為止。對最后的偽和與局部進位通過進位傳遞加法器相加得出真正的結果。在這種處理方式中,每列中求偽和的操作是并行完成的。由于采用全加器作為加法部件,每次能將3個權為20的輸入信號經處理后得到一個權為21的局部進位信號和一個權為20的偽和信號,這樣操作數的數目減少1/ 3,將產生的中間偽和也按照這種方式處理,經過時間為O(log3/ 2 N) 的處理后可以得到最后的偽和與局部進位信號。
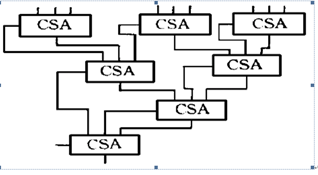
圖16 華萊士樹加法樹示意圖

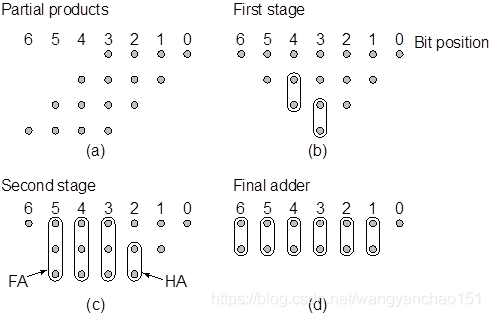
圖17 4x4位華萊士樹乘法器實現圖
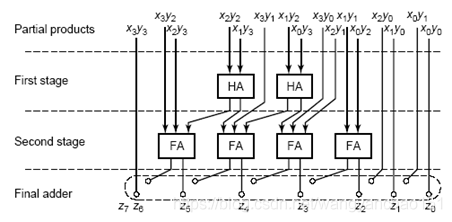
圖18 4x4位華萊士樹乘法器架構圖
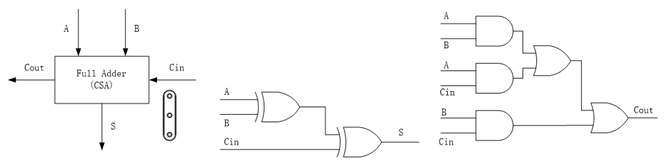
圖19 保留進位加法器(CSA)
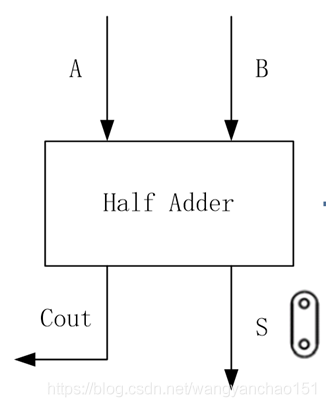
圖20 半加器
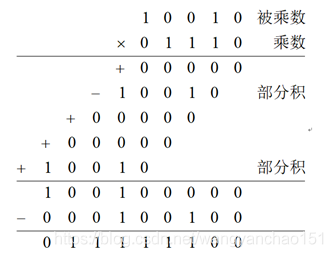
布斯算法(Booth’s Algorithm)的做法是對乘數編碼以計算出乘法運算的結果,主要的想法在于乘數中連續的1,這些1會造成被乘數的連加。
但是,乘數01110又可表示為10000-00010,這樣可將部分積減少為2個。當我們遇到乘數中連續的’1’時(從右往左看),第一個’1’減去被乘數,最后一個’1’后面的’0’則加上被乘數。
布斯編碼的核心在于對連續的’1’字串進行頭、中、尾三段的分段處理(從右往左看)。當然,’0’字串由于本身就無須進行運算,所以不必理會。
華萊士乘法器
先介紹陣列乘法器,我們用筆計算乘法時,第一個操作數為被乘數(multiplicand),第二個操作數為乘數(multiplier)。而乘數中的每一個位和被乘數做相乘的運算后的結果稱之為部分乘積(partial product),而將所有的部分乘積相加之后,其運算結果稱為乘積(product)。如:1000×1001為例,

通過以上的示例我們可以發現如下四點:
第一:當乘數的位數字為1 時,我們可以將被乘數的值直接放置適當的位置。而適當的位置是依乘數的第幾個位和被乘數做運算之后所放的位置。
第二:當乘數的位數字為0 時,我們可以將0 放置適當的位置, 以作為部分乘積。
第三:我們利用筆和紙計算的乘法,在硬件中使用與門來實現。例如:1000 ×1中,乘數1 和每一個被乘數的位都個別做與運算,其結果為1000 正是我們所要的結果。由此可知我們只需用與門就可以完成我們所要的乘法。
第四:當部分乘積都運算完成后,使用加法來完成最終的乘法結果運算。
根據以上四點的說明,我們可以運用最簡單、最直觀的方式來描述固定點乘法器的電路描述。我們使用與門來做部分積運算,使用全加器(Full adder)來運算部分積的最終結果。因為作加法時,會有進位問題,且上一位所產生的進位也非常重要,所以只有全加器能滿足我們的加法要求。圖13所示為有符號位的6×6固定點乘法器的架構圖。
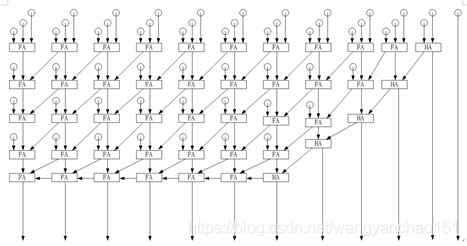
圖13 6×6固定點乘法器架構圖
原文標題:三種高速乘法器的FPGA實現及性能比較
文章出處:【微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
-
FPGA
+關注
關注
1643文章
21980瀏覽量
614519 -
集成電路
+關注
關注
5420文章
11970瀏覽量
367338 -
加法器
+關注
關注
6文章
183瀏覽量
30627 -
乘法器
+關注
關注
9文章
211瀏覽量
37844
原文標題:三種高速乘法器的FPGA實現及性能比較
文章出處:【微信號:gh_9d70b445f494,微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
乘法器對數運算電路應用

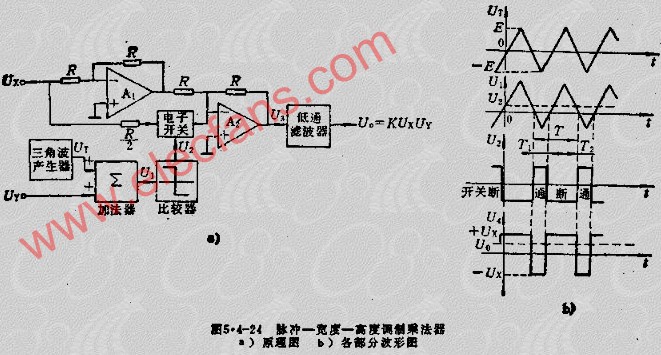
脈沖-寬度-高度調制乘法器
基于IP核的乘法器設計
基于FPGA的高速流水線浮點乘法器設計與實現
乘法器的使用方法你知道哪些?
使用verilogHDL實現乘法器
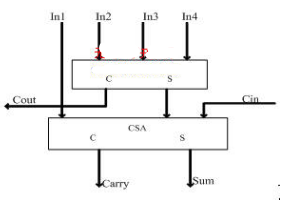
如何實現一個四輸入乘法器的設計
乘法器原理_乘法器的作用

采用Gillbert單元如何實現CMOS模擬乘法器的應用設計
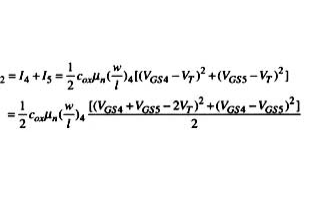





 三種高速乘法器實現原理
三種高速乘法器實現原理











評論