微波諧振器是微波工程里使用非常普遍的一類無源器件，它可以構成振蕩器、濾波器的一部分，也可以用于各種測量或傳感系統中（比如介電常數、表面阻抗測量系統，溫濕度傳感系統等）。諧振頻率和品質因子（簡稱Q值）是衡量微波諧振器特性最為關鍵的參數。本文對微波諧振器的Q值獲取方法進行探討。總體上而言，Q值提取方法可以分為頻域法和時域法。3dB法是最具代表性的頻域方法，它需要首先獲取3dB帶寬，然后計算得到Q值。而時域法則是通過觀察激勵信號源突然關閉后，依據諧振器輸出端口信號的時變特性來獲取Q值。本文介紹頻域方法。常見的微波諧振器有單端口和雙端口兩種。前者需要測量諧振器的S11來獲取Q值，而后者則是通過測量S21來獲取Q值。本文探討雙端口諧振器的Q值提取方法。

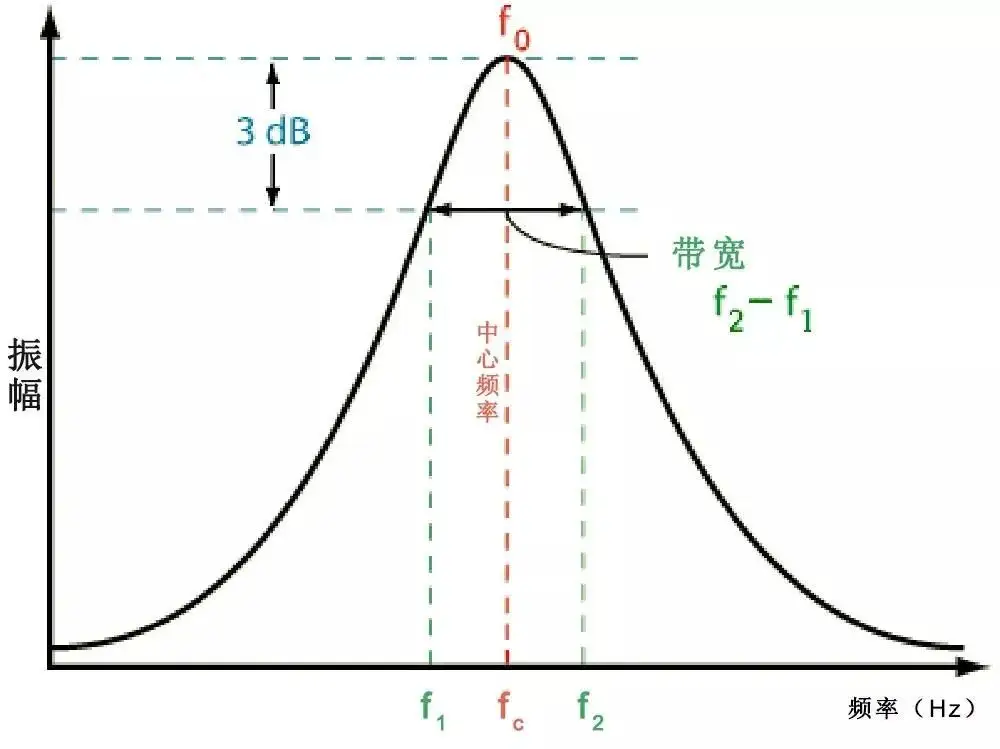
傳統的3dB法提取Q值的過程如下圖所示：橫坐標為頻率，縱坐標為S21幅度，S21幅度最大值對應的頻率即為諧振頻率f0，然后分別在f0的左側和右側找到3dB帶寬頻點f1和f2，這兩個頻點對應的S21幅度比S21幅度的最大值低3dB，到此即可得到3dB帶寬為(f2-f1)，于是諧振器的有載Q值可由QL=f0/(f2-f1)計算得到，無載Q值Q0可由有載Q值和S21幅度最大值|S21|max按照Q0=QL/(1-|S21|max)計算得到（注意，這里的|S21|max須是線性值，其數值為0至1之間的某個數）。舉例如下，假設諧振器諧振頻率為3GHz，3dB帶寬為5MHz，則有載Q值為3GHz/5MHz=600，又假設諧振器在諧振頻率處的插損為40dB，則|S21|max=10^(-40/20)=0.01，于是無載Q值Q0=600/(1-0.01)=606。

依據上述3dB法求解Q值的過程，如果獲得了雙端口諧振器的S21幅度隨頻率變化的數據，可以利用下述MATLAB代碼求解Q值：

simu_data01=load( 'S21_dB_freq.txt'); %導入S21數據,第一列為頻率,第二列為dB形式的S21

f=simu_data01(:,1); %頻率

S21=simu_data01(:,2); % S21，dB

[S21m, S21m_location]=max(S21);%找到S21幅度最大值及其位置

f_center=f(S21m_location); %諧振頻率；

S21dB_center=S21(S21m_location);%找到dB形式的S21幅度最大值

S21_center=10^(S21dB_center/20);%找到線性形式的S21幅度最大值

%找到諧振頻率左側3dB帶寬對應的頻點

a01=find(S21(1:S21m_location)-S21m>-3.1,1);

a02=find(S21(1:S21m_location)-S21m>-0.1,1);

f_low=interp1(S21(a01:a02),f(a01:a02),S21m-3,'spline');

%找到諧振頻率右側3dB帶寬對應的頻點

a01=find(S21(S21m_location:length(S21))-S21m<-3.1,1);

a02=find(S21(S21m_location:length(S21))-S21m<-0.1,1);

f_up=interp1(S21(a02+S21m_location-1+1:a01+S21m_location-1),f(a02+S21m_location-1+1:a01+S21m_location-1),S21m-3,'spline');

%計算有載Q值

Q_L=f_center/(f_up-f_low);

%計算無載Q值

g=S21_center/(1-S21_center); % for series RLC circuit

% g=(1-S21_center)/S21_center; % for parallel RLC circuit

Q_unload=Q_L*(1+g);

用傳統的3dB法測量Q值時，需要進行掃頻測試，且要求掃頻帶寬至少是3dB帶寬的一定倍數（比如1.5倍或更大）。因此，這種測試方法對掃頻信號源的掃頻帶寬有一定的要求，而且較大的掃頻帶寬一般也就意味著更長的測試時間。所以，如果能夠減小掃頻帶寬，則可能有助于降低掃頻源的成本并縮短掃頻時長也就是縮減測試時長，進而降低測試成本。本文即探討此種可能性。

在文獻《Measurement of resonant frequency and quality factor of microwave resonators: Comparison of methods》中，給出了雙端口諧振器的S21幅度隨頻率變化的規律如下：

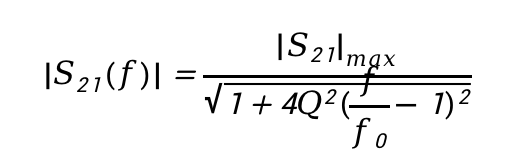
由上式可知，如下3個參數決定了諧振器傳輸曲線的形狀和位置：S21幅度最大值、品質因子、諧振頻率。如果做一些計算實驗，不難發現，參數S21幅度最大值影響傳輸曲線在縱坐標上的位置，品質因子影響傳輸曲線的“胖瘦”，而諧振頻率影響傳輸曲線在橫坐標上的位置。接下來，我們首先檢驗上式是否能夠描述常見諧振器的傳輸曲線；然后，我們利用上式構造了若干諧振器傳輸曲線，然后觀察諧振器傳輸曲線的1dB帶寬是否和3dB帶寬存在某種定量關聯性。如果這種關聯性是存在的，則可以通過1dB帶寬的測量間接獲取3dB帶寬，并最終實現1dB法獲取諧振器Q值。

這里，我們選取了常見的圓柱諧振腔、同軸諧振腔、矩形諧振腔、微帶環形諧振器以及準光腔作為演示案例。

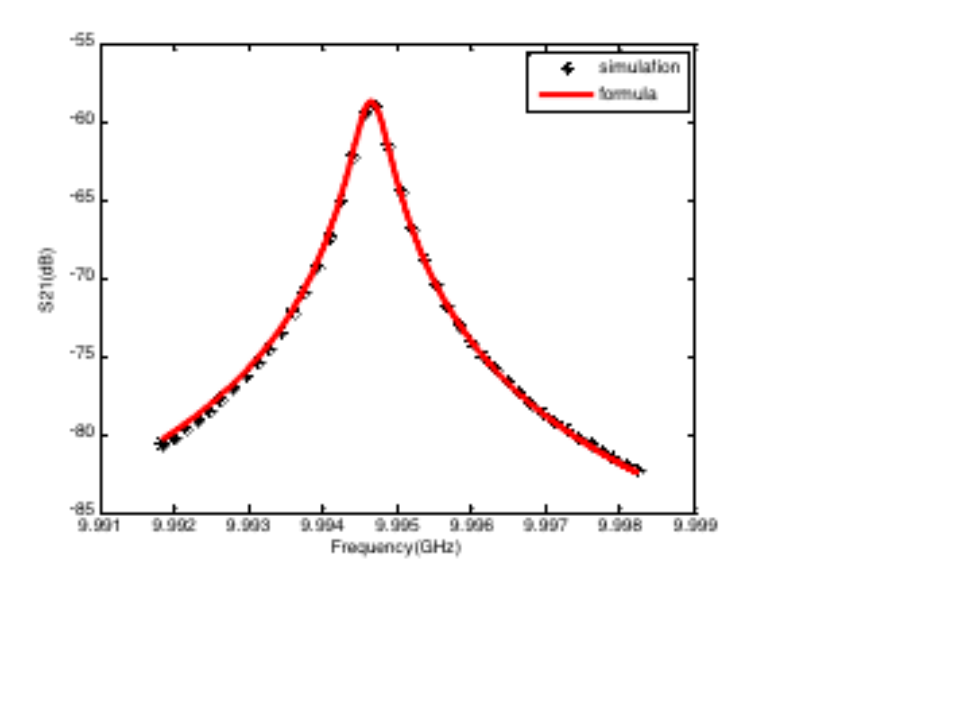
第一個圓柱諧振腔的三維剖面模型及其傳輸曲線仿真結果如下所示。這是一個諧振頻率約為10GHz的諧振腔。

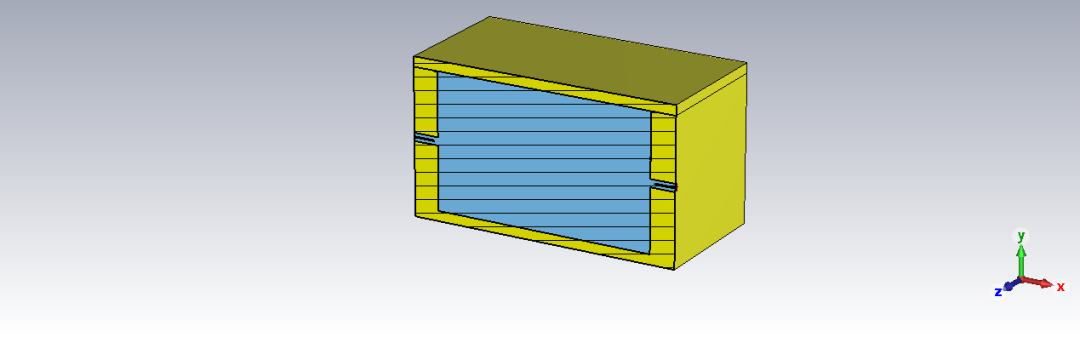
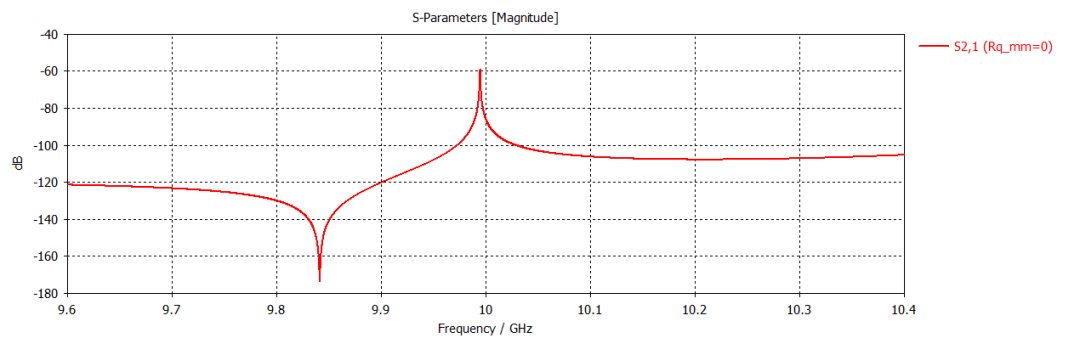
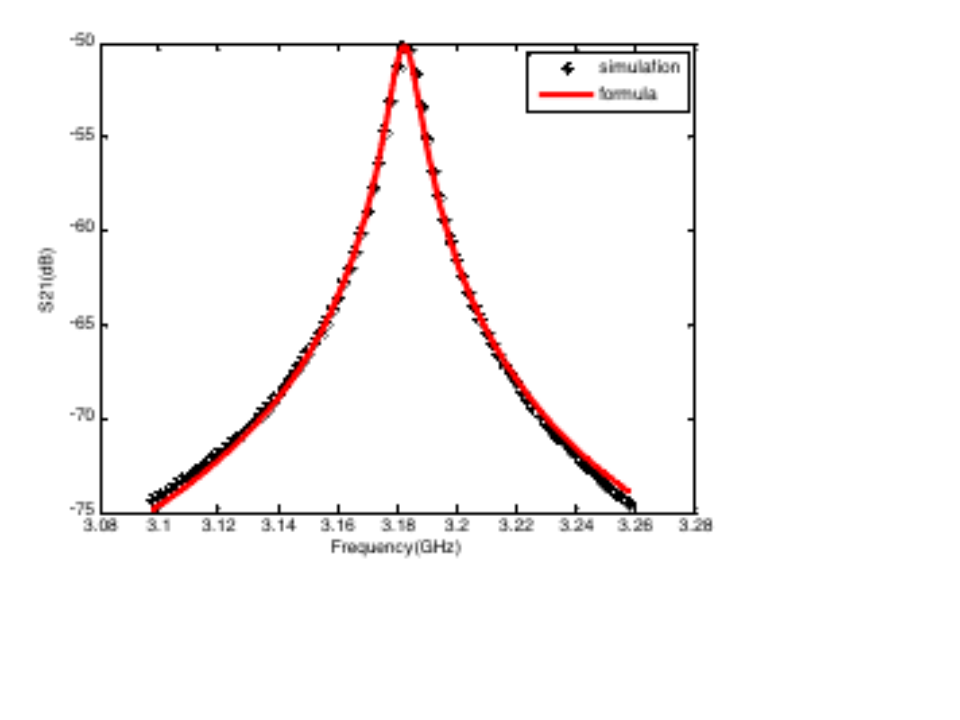
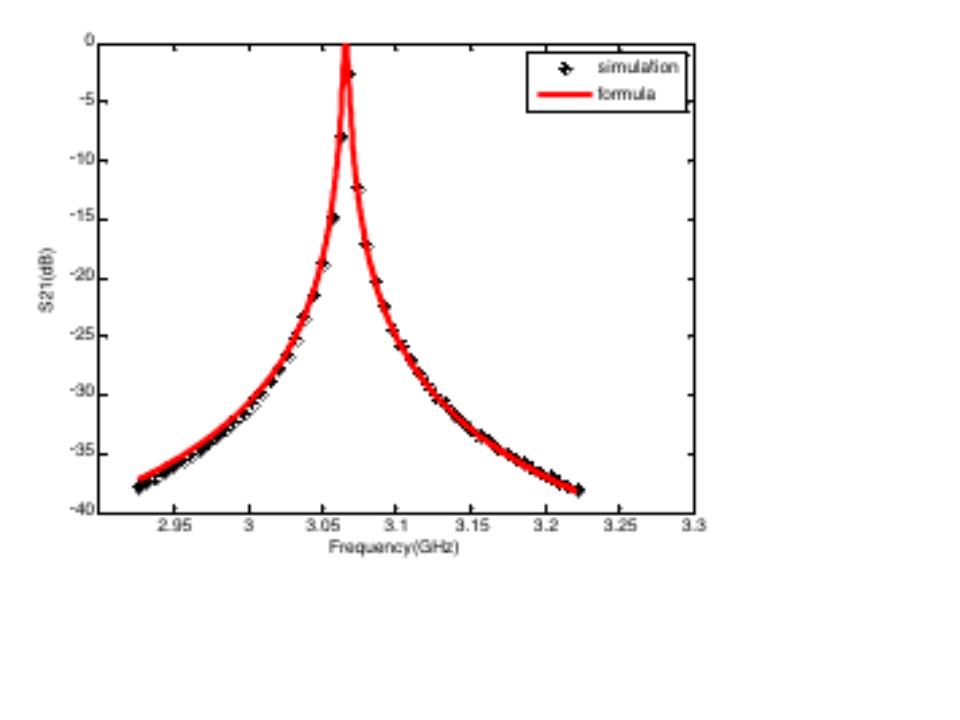
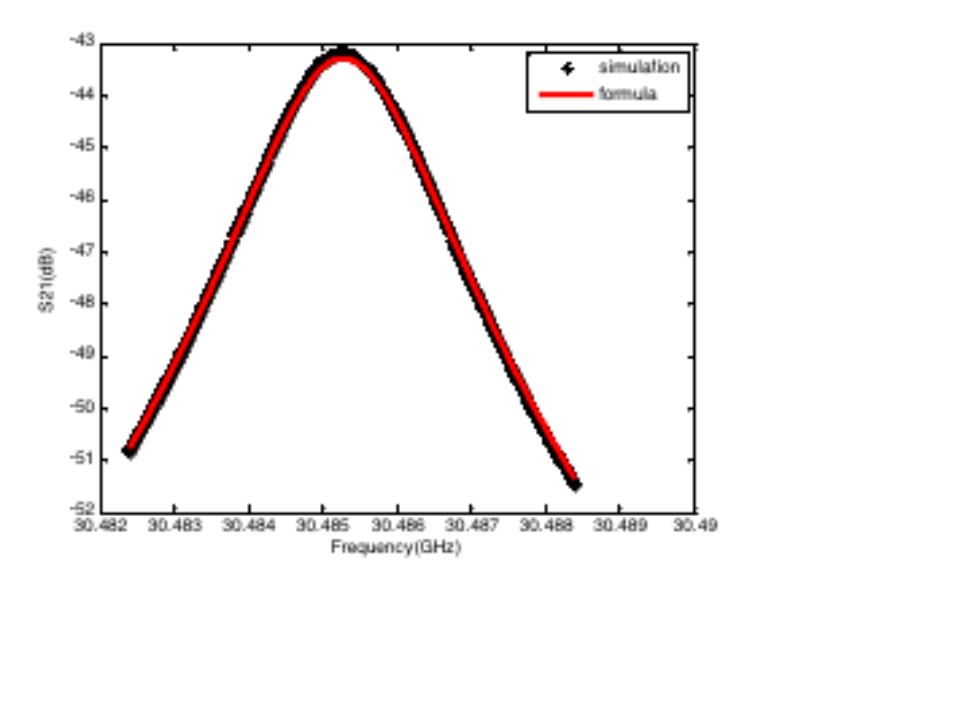
運用前述公式，對上圖得到的諧振峰仿真結果進行擬合，所得結果如下。可以看到，擬合結果與仿真結果吻合良好。其余幾種腔體也得到了類似的擬合效果，這表明前述公式可以用于描述雙端口諧振器的傳輸曲線。

第二個圓柱諧振腔案例是一個諧振頻率約為18GHz的腔體，其相關結果如下所示。

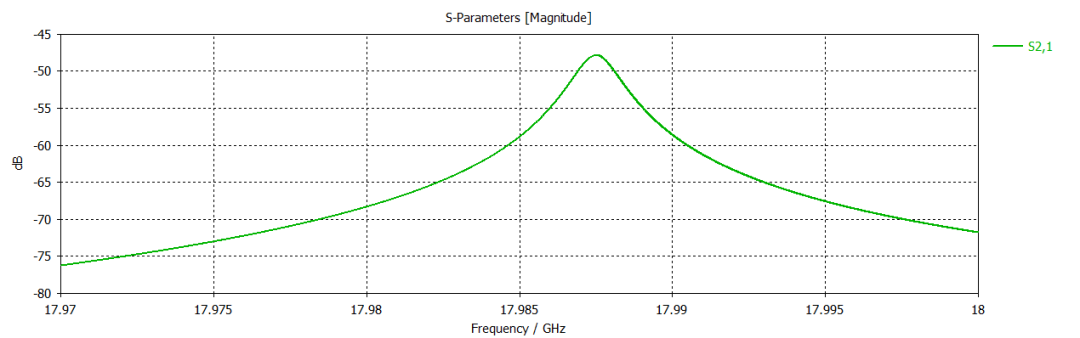
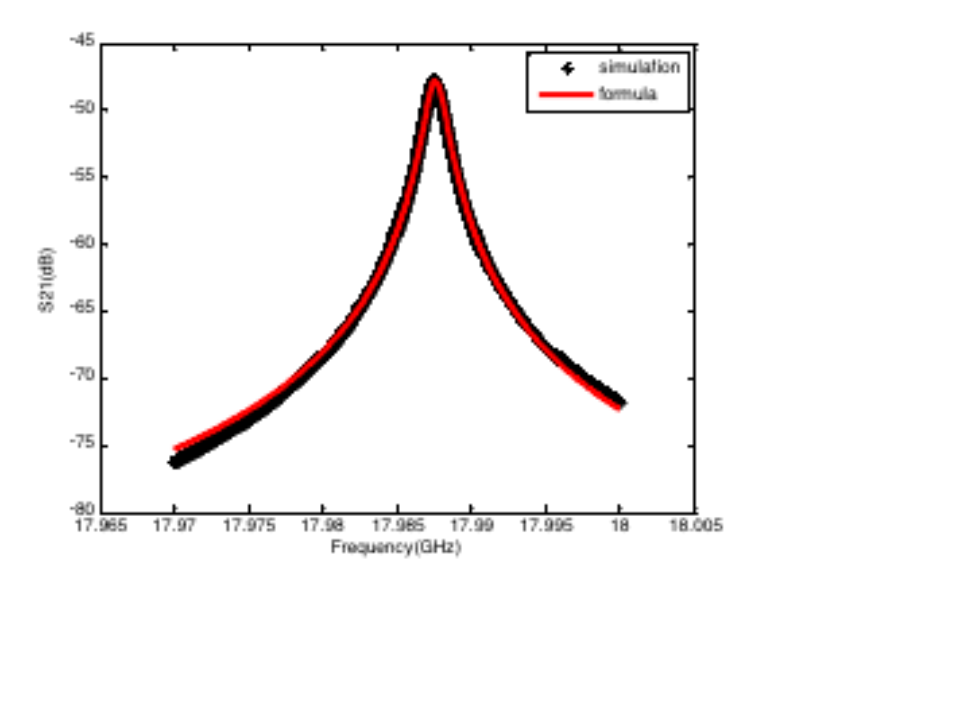
第三個圓柱諧振腔案例仍是一個諧振頻率約為18GHz的腔體，但是該腔體的上端板排布有周期性的方孔，其模型及相關結果如下所示。

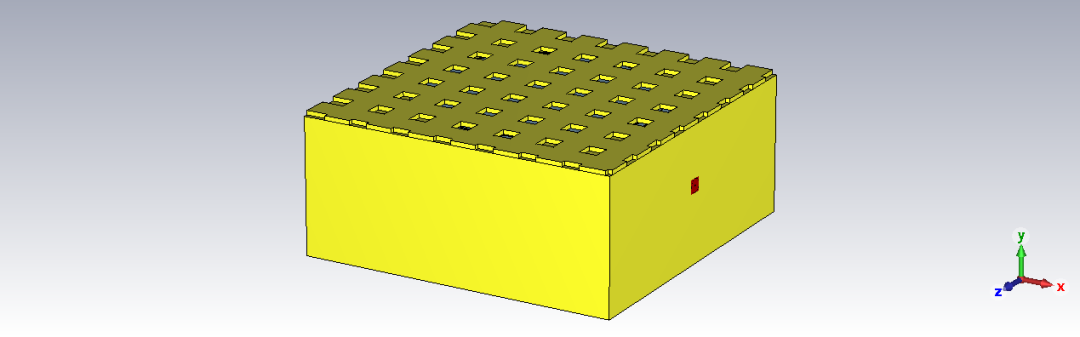
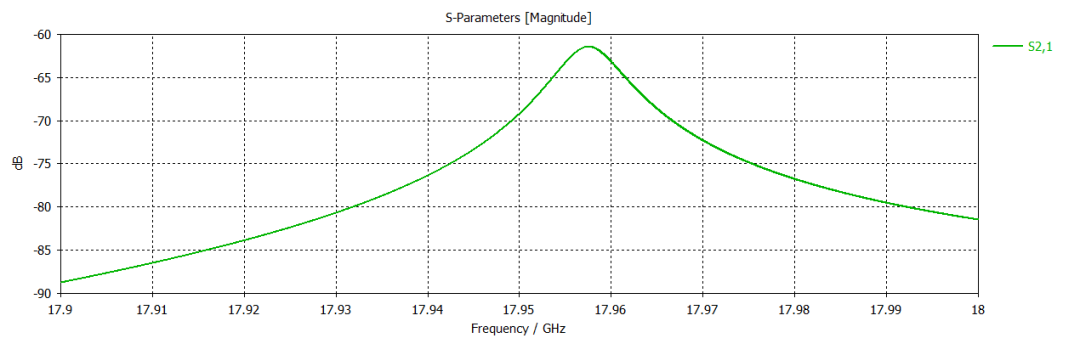
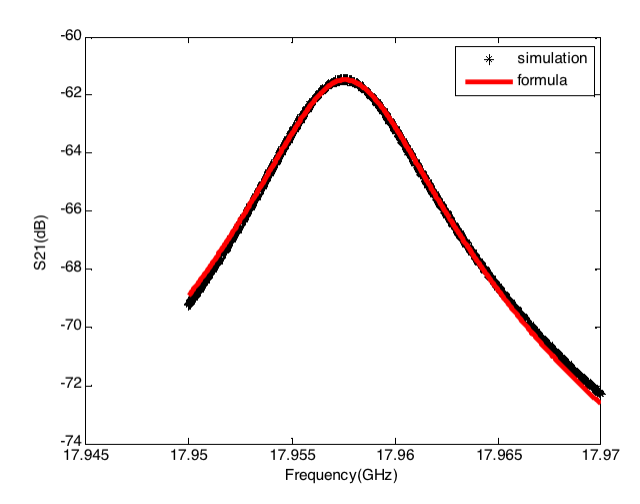
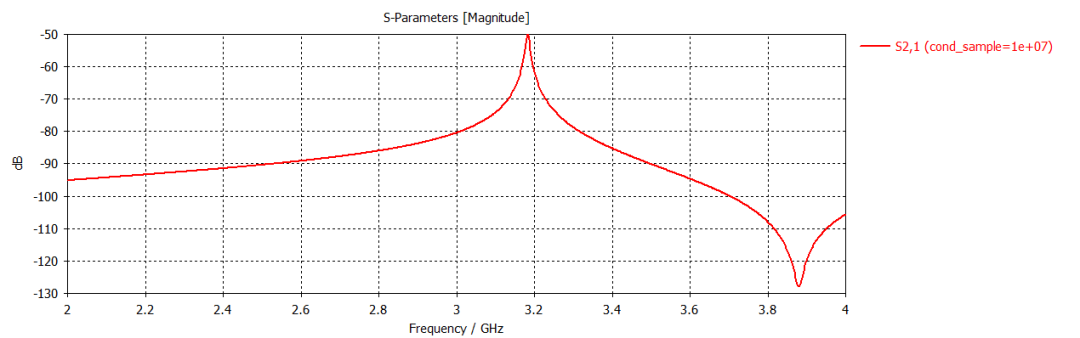
同軸諧振腔案例的相關結果如下所示。這是一個諧振頻率約為3.2GHz的腔體。

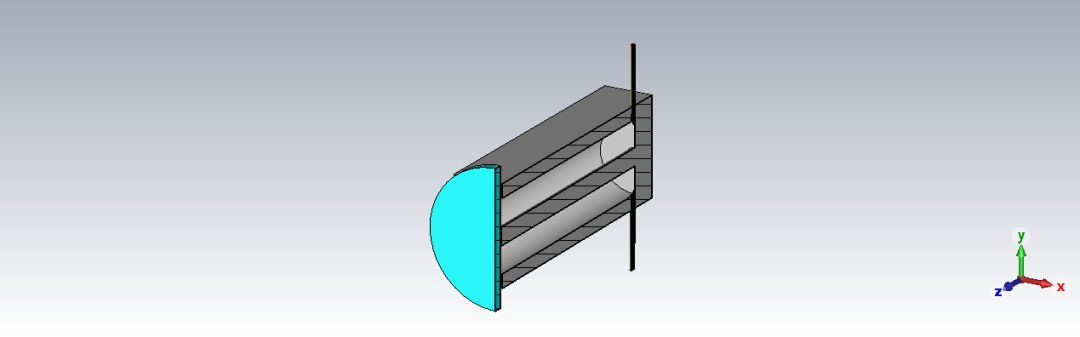
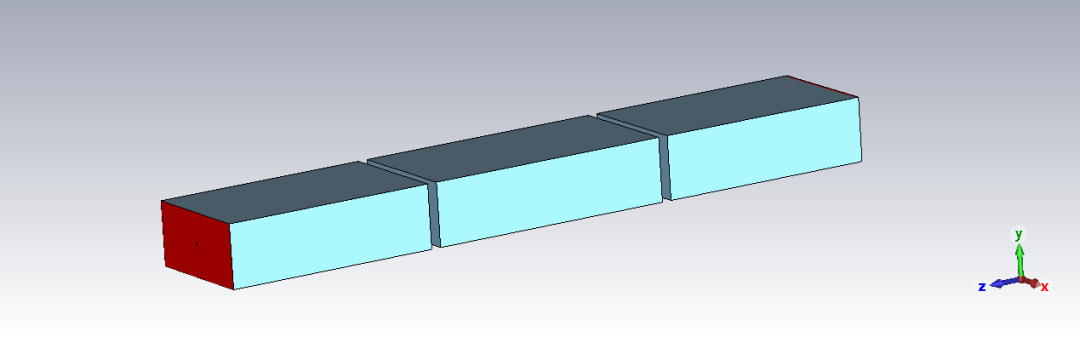
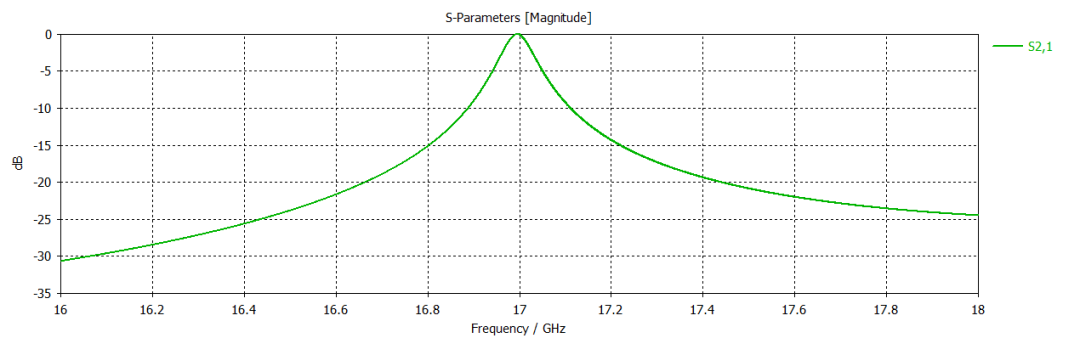
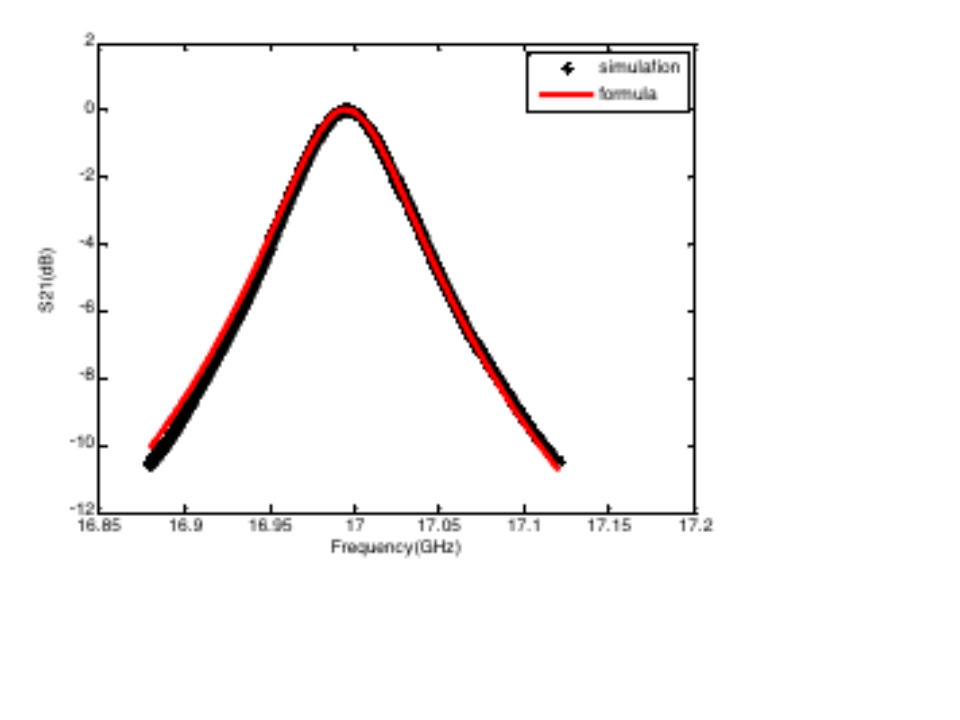
矩形諧振腔案例的相關結果如下所示。這是一個諧振頻率約為17GHz的腔體。

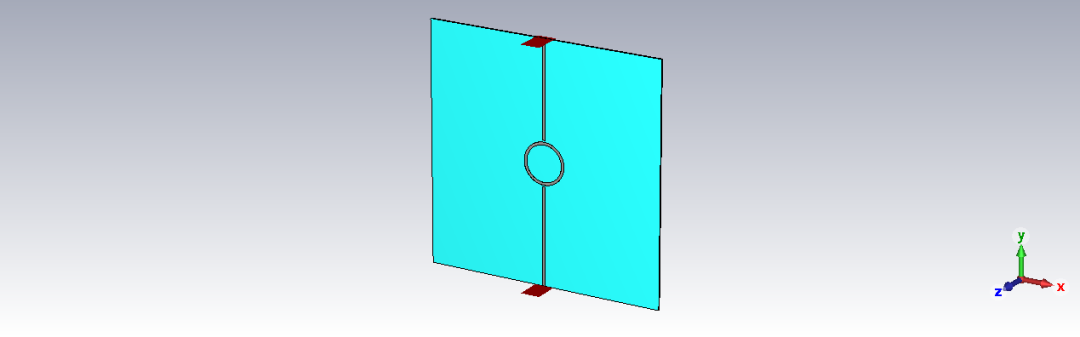
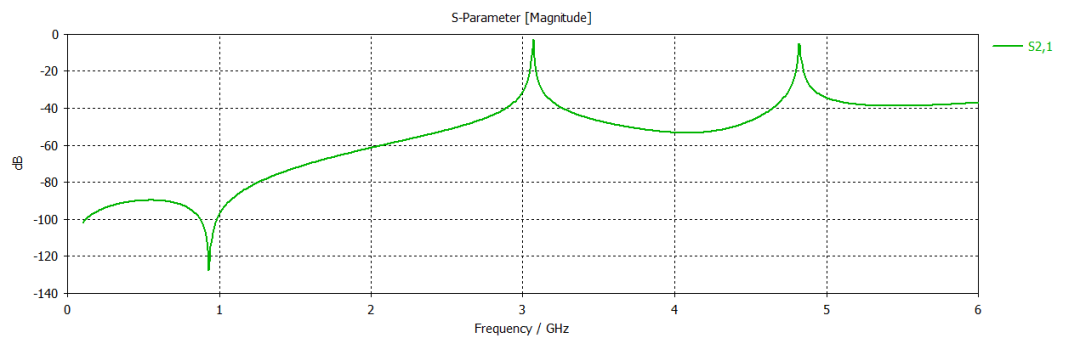
微帶環形諧振器案例的相關結果如下所示。在CST仿真頻段內出現了2個諧振峰，我們對第一個諧振峰也就是3GHz附近的諧振峰進行了擬合。

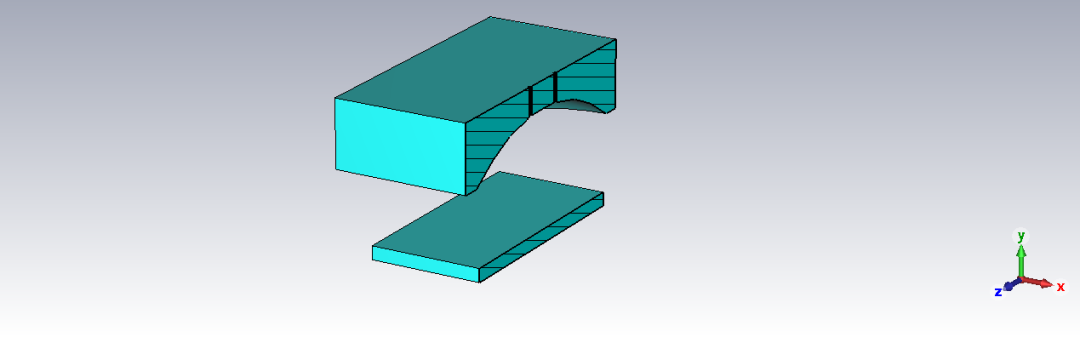
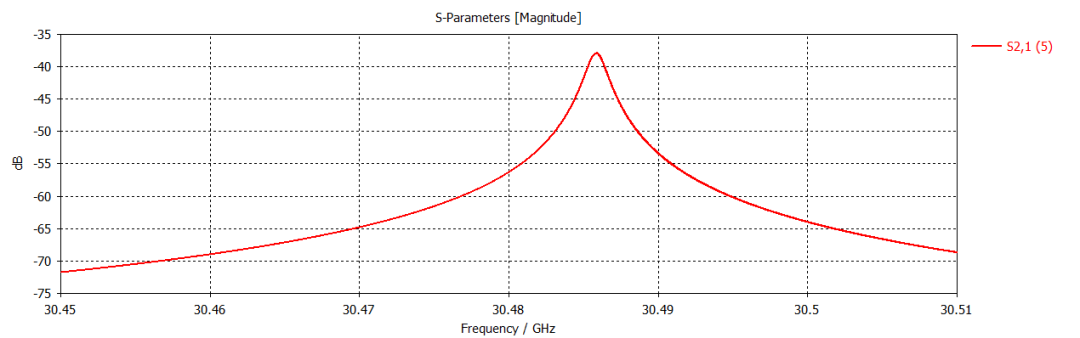
準光腔案例的相關結果如下所示。其諧振頻率約為30GHz。

通過上述7個案例，表明前述公式可以描述常見諧振器的傳輸曲線。以下是上述擬合過程所采用的典型MATLAB代碼：

S21_data_simu=textread('simulation_data.txt','','headerlines',3);%導入CST仿真數據

nn01=2450;%設定擬合頻段的起始頻點

nn02=2490;%設定擬合頻段的終止頻點

freq_simu=S21_data_simu(nn01:nn02,1);%頻率

S21_dB_simu=S21_data_simu(nn01:nn02,2);% dB形式的S21

S21_linear_simu=10.^(S21_dB_simu./20);%線性形式的S21

figure(1);plot(freq_simu,S21_dB_simu,'k*');hold on;%繪制仿真數據

%以下是掃參擬合

a_sweep=linspace(0.0011,0.0013,100);

b_sweep=linspace(1e4,3e4,50);

c_sweep=linspace(9.994,9.995,50);

error01=1e4;

opti_num=[0 0 0];

for nnfor01=1:length(a_sweep)

for nnfor02=1:length(b_sweep)

for nnfor03=1:length(c_sweep)

a=a_sweep(nnfor01);

b=b_sweep(nnfor02);

c=c_sweep(nnfor03);

x=freq_simu;

y=a./sqrt(1+4.*b.^2.*(x./c-1).^2);

error_for01=mean(abs(S21_linear_simu-y));

if error_for01

error01=error_for01;

opti_num=[nnfor01 nnfor02 nnfor03];

end

end

end

end

a_opti=a_sweep(opti_num(1));

b_opti=b_sweep(opti_num(2));

c_opti=c_sweep(opti_num(3));

%依據掃參擬合得到的擬合系數計算傳輸曲線并繪圖

x=linspace(min(freq_simu),max(freq_simu),1e3);

y_opti=a_opti./sqrt(1+4.*b_opti.^2.*(x./c_opti-1).^2);

figure(1);plot(x,20.*log10(y_opti),'r-','linewidth',3);

xlabel('Frequency(GHz)');ylabel('S21(dB)');

legend('simulation','formula');

接下來，我們利用前述公式構造若干傳輸曲線并觀察1dB帶寬和3dB帶寬的關系。S21幅度最大值取值0.1、諧振頻率取值3GHz、品質因子從10掃描至1000萬時，得到的1dB帶寬與3dB帶寬之比如下圖——恒為0.51。當S21幅度最大值、諧振頻率為其它取值時，得到了相同的結果——1dB帶寬與3dB帶寬之比恒為0.51。這意味著，實際測量諧振器Q值時，可以先測得1dB帶寬，然后用此1dB帶寬乘以系數1/0.51=1.961，即可得到諧振器的3dB帶寬，進而得到諧振器Q值。換言之，1dB帶寬約為3dB帶寬的一半。這樣，掃頻源的掃頻范圍可以減半，或者說掃頻時長可以縮至原先的一半。

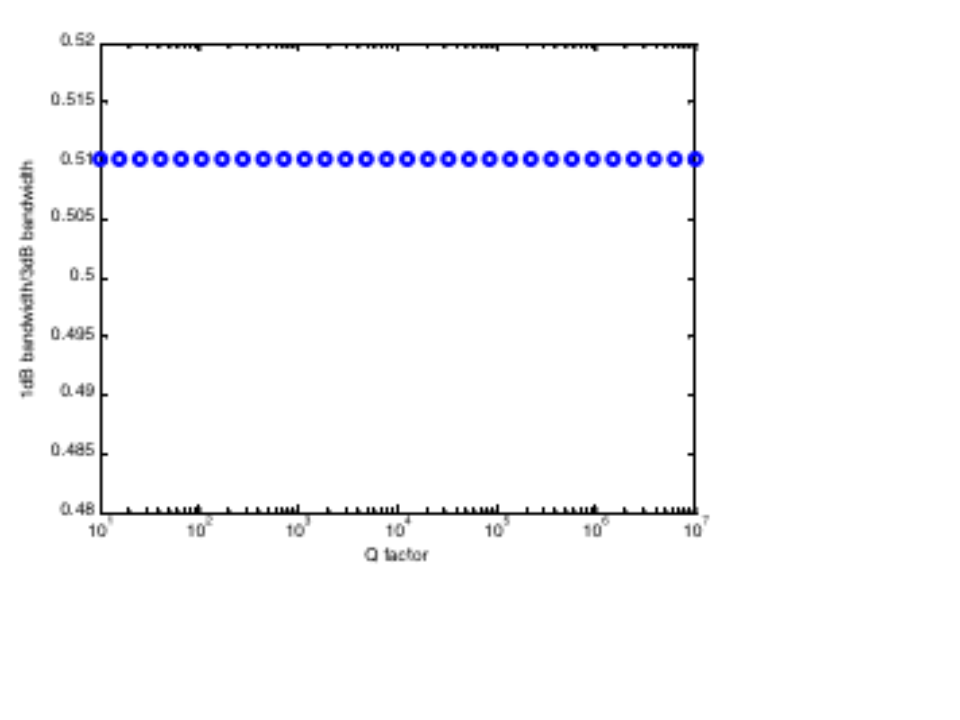
上圖對應的MATLAB代碼如下：

Q_sweep=logspace(1,7,30);

for nn01=1:length(Q_sweep)

Q=Q_sweep(nn01);

f0_GHz=3;

abs_S21=0.1;

S21_dB=20*log10(abs_S21);

bandwidth01=f0_GHz/Q;

f_GHz=linspace(f0_GHz-2*bandwidth01,f0_GHz+2*bandwidth01,1e3);

real_S21=abs_S21./(1+4.*Q.^2.*(f_GHz./f0_GHz-1).^2);

imag_S21=-abs_S21.*2.*Q.*(f_GHz./f0_GHz-1)./(1+4.*Q.^2.*(f_GHz./f0_GHz-1).^2);

mag_S21=sqrt(real_S21.^2+imag_S21.^2);

mag_S21_dB=20.*log10(mag_S21);

[S21_dB_max,S21_dB_num]=max(mag_S21_dB);

% 3dB

f_GHz_left_3dB=interp1(mag_S21_dB(1:S21_dB_num-1),f_GHz(1:S21_dB_num-1),S21_dB_max-3,'spline');

f_GHz_righ_3dB=interp1(mag_S21_dB(S21_dB_num+1:length(f_GHz)),f_GHz(S21_dB_num+1:length(f_GHz)),S21_dB_max-3,'spline');

delta_f_3dB=f_GHz_righ_3dB-f_GHz_left_3dB;

Q_3dB(nn01)=f0_GHz/delta_f_3dB;

% 1dB

f_GHz_left_1dB=interp1(mag_S21_dB(1:S21_dB_num-1),f_GHz(1:S21_dB_num-1),S21_dB_max-1,'spline');

f_GHz_righ_1dB=interp1(mag_S21_dB(S21_dB_num+1:length(f_GHz)),f_GHz(S21_dB_num+1:length(f_GHz)),S21_dB_max-1,'spline');

delta_f_1dB=f_GHz_righ_1dB-f_GHz_left_1dB;

Q_1dB(nn01)=f0_GHz/delta_f_1dB;

end

ratio_Q=Q_3dB./Q_1dB;

semilogx(Q_sweep,ratio_Q,'bo','linewidth',3);

xlabel('Q factor');ylabel('1dB bandwidth/3dB bandwidth');

axis([10,1e7,0.48,0.52]);

審核編輯：湯梓紅