1、多層神經網絡復雜化，提升效率成為新挑戰

神經網絡從感知機發展到多層前饋神經網絡，網絡變得越來越復雜。如上一篇 機器學習中的函數（2）- 多層前饋網絡巧解“異或”問題，損失函數上場優化網絡性能 討論針對前饋神經網絡我們的目標是要讓損失函數達到最小值，這樣實際輸出和預期輸出的差值最小，利用最小化損失函數提升分類的精度。顯然，采用“窮舉”找優參數的方法不是聰明的選擇，費時費力。我們現在面臨的問題和挑戰變成，如何找到一個高效的方法從眾多網絡參數（神經元之間的連接權值和偏置）中選擇最佳的參數？這就是我們即將一起學習討論的話題。

在研究復雜問題之前，我們先要弄清楚幾個基礎概念，包括“凸函數”，“梯度”，“梯度下降”。

2、基礎概念：凸函數和凸曲面、梯度和梯度下降

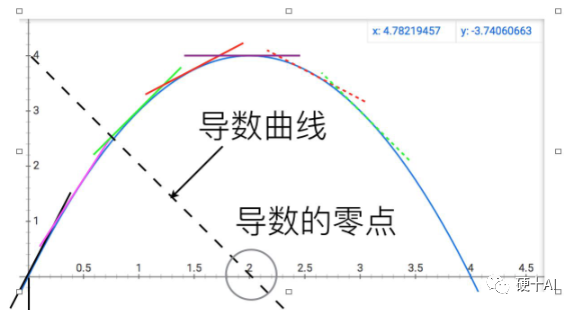
討論這些概念前必須向偉大的牛頓致敬，當科學發展到伽利略和開普勒那個年代，人們就在物理學和天文學中遇到很多求一個函數的最大值或最小值，即最優化問題，比如計算行星運動的近日點和遠日點距離等。如何系統地解決最優化問題？牛頓創造性的給出了答案，他的偉大之處在于，他不像前人那樣，將最優化問題看成是若干數量比較大小的問題，而看成是研究函數動態變化趨勢的問題 。如下圖，牛頓對比拋物線和它的導數（虛的直線），發現曲線達到最高點的位置，就是切線變成水平的位置，或者說導數變為0的位置呢。他把比較數大小的問題，變成了尋找函數變化拐點的問題，同時發明導數這種工具將這兩個問題等同起來，利用導數這個工具求最大值問題就變成了解方程的問題，你看微積分這種強大的數學工具在神經網絡中多重要啊。

（1）凸函數和凸曲面

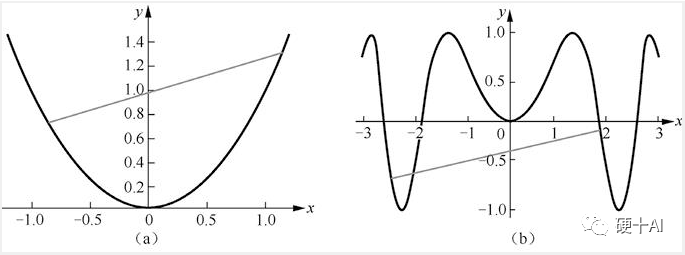
凸函數的直觀認識：下圖中上述［圖a］是凸函數圖像，［圖b］是非凸函數圖像，“任意兩點連接而成的線段與函數沒有交點”即為凸函數。

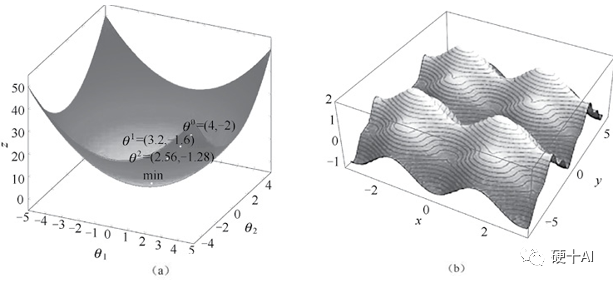
從凸曲面與非凸曲面理解最小值和局部最小值：凸函數的局部極小值就是全局最小值，如下圖中【圖a】凸曲面中無論彈珠起始位置在何處，彈珠最終都會落在曲面的最低點，而這個極小值恰好是全局最小值。而非凸函數求導獲得的極小值不能保證是全局最小值，如【圖b】非凸曲面中彈珠仍然會落在曲面的某個低點，但有可能不是全局的最低點。

（2）梯度和梯度下降法

梯度（gradient）的本質是一個向量（有大小和方向兩個要素），表示某一函數在該點處的方向導數沿著該方向取得最大值，即函數在該點處沿著此梯度的方向變化最快，變化率最大。為求得這個梯度值會用到“偏導”的概念，“偏導”的英文是“partial derivatives”，若譯成“局部導數”更易理解，對于多維變量函數而言，當求某個變量的導數時，就是把其他變量視為常量，然后對整個函數求其導數，由于這里只求一個變量，即為“局部”。接著把這個對“一個變量”求導的過程對余下的其他變量都求一遍導數，再放到向量場中，就得到了這個函數的梯度。

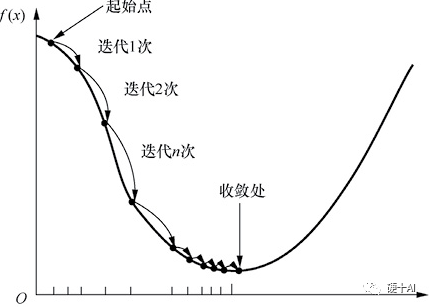
梯度下降法（Gradient descent）是最常見的一種最優化問題求解方法。打個比方，假設一個高度近視的人在山的某個位置上（定義為起始點），他計劃從從山上走下來，也就是走到山的最低點。這個時候，他可以以起始點為基準，尋找這個位置點附近最陡峭的地方，然后朝著山的高度下降的方向走，如此循環迭代，最后就可以到達山谷位置。梯度下降過程示意如下圖所示，當我們沿著負梯度方向進行迭代的時候“每次走多大的距離”是需要算法工程師去調試的，即算法工程師就是要調試合適的“學習率”，從而找到“最佳”參數。如果碰到極大值問題，則可以將目標函數加上負號，從而將其轉換成極小值問題來求解。

3、BP算法提升效率，讓人工智能再次進

如本文開頭提到的，上世紀70年代多層神經網絡出現后，面臨重大的挑戰是增加神經網絡的層數雖然可為其提供更大的靈活性，讓網絡能解決更多的問題，但隨之而來的數量龐大的網絡參數的訓練，這是制約多層神經網絡發展的一個重要瓶頸。這時誤差逆傳播（error BackPropagation， 簡稱BP）算法出現了。現在提及BP算法時，常常把保羅·沃伯斯（PaulWerbos）稱作BP算法的提出者，杰弗里?辛頓（Geoffrey Hinton）稱作BP算法的推動者。

1974年，沃伯斯（圖a）在哈佛大學取得博士學位，在他的博士論文里首次提出了通過誤差的反向傳播來訓練人工神經網絡，沃伯斯的研究工作，為多層神經網絡的學習、訓練與實現，提供了一種切實可行的解決途徑。

1986年，辛頓教授（圖b）和他的團隊優化了BP算法，吻醒了沉睡多年的“人工智能”公主，讓人工智能研究再次進入繁榮期。

BP算法其實并不僅僅是一個反向算法，而是一個雙向算法，它其實是分兩步走①正向傳播信號，輸出分類信息；②反向傳播誤差，調整網絡權值 。

BP 算法基于梯度下降（gradient descent）策略，以目標的負梯度方向對參數進行調整，采用“鏈式法則”（鏈式法則用于求解復合函數的導數，復合函數導數是構成復合的函數在相應點的乘積，就像鎖鏈一環扣一環，所以稱為鏈式法則）。

BP算法的工作流程拆解開如下，對于每個訓練樣例BP算法執行的順序是

先將輸入示例提供給輸入層神經元，然后逐層將信號前傳，直到產生輸出層的結果。

然后計算輸出層的誤差，再將誤差逆向傳播至隱層神經元。

最后根據隱層神經元的誤差來對連接權和閾值進行調整。

該迭代過程循環進行，直到達到某些停止條件為止，例如訓練誤差已達到一個很小的值。實際應用中BP算法把網絡權值糾錯的運算量，從原來的與神經元數目的平方成正比，下降到只和神經元數目本身成正比，效率和可行性大大提升，而這個得益于這個反向模式微分方法節省的計算冗余。

4、BP算法的缺陷

BP算法在很多場合都很適用，集“BP算法”之大成者當屬Yann LeCun（楊立昆），紐約大學教授2018年還拿過圖靈獎，擔任過Facebook首席人工智能科學家。1989年，LeCun就用BP算法在手寫郵政編碼識別上有著非常成功的應用，訓練好的系統，手寫數字錯誤率只有5%。LeCun借此還申請了專利，開了公司，發了筆小財。但如前所述，BP算法的缺點也很明顯，在神經網絡的層數增多時，很容易陷入局部最優解，亦容易過擬合。20世紀90年代，VladimirVapnik（萬普尼克）提出了著名的支持向量機（Support Vector Machine，SVM），雖然SVM是一個特殊的兩層神經網絡，但因該算法性能卓越，具有可解釋性，且沒有局部最優的問題，在圖像和語音識別等領域獲得了廣泛而成功的應用。在手寫郵政編碼的識別問題上，LeCun利用BP算法把錯誤率降到5%左右，而SVM在1998年就把錯誤率降低至0.8%，這遠超越同期的傳統神經網絡算法。這使得很多神經網絡的研究者轉向SVM的研究，從而導致多層前饋神經網絡的研究逐漸受到冷落，在某種程度上萬普尼克又把神經網絡研究送到了一個新的低潮期。

神經網絡又是如何度過這個低谷期，快速進入到下一個繁榮時代的呢？