導讀:上一篇《彈性地基梁matlab有限元編程,以雙排樁支護結構計算為例》引起了Matlab有限元編程學習者的共鳴。今天我想和大家討論一下熱應力問題(六面體單元)matlab有限元編程問題。
本案例主要介紹熱應力問題的matlab有限元編程及原理。熱應力也叫溫度應力,后文提到的熱應變也叫溫度應變。這里需要與傳熱問題的有限元分析進行區分:可以認為傳熱分析是進行熱應力分析的前提條件,通過傳熱分析來確定溫度場,在獲得溫度場的基礎上,計算所產生的熱應力。所以本文為闡述熱應力問題前提是假定溫度場是已知的,我們并不關心溫度場是如何得到的,那是熱傳導要解決的問題,在這個已知的溫度場作用下,由于熱脹冷縮會產生響應的熱應變進而產生熱應力,如何求解這個熱應力,這就是我們這次課程要解決的問題。
如圖1所示,本案例的分析對象為一個兩端固定約束的四棱柱受不同方向的熱應變作用下產生的應力應變,在用有限元方法求解熱應力問題時,溫度作用可以等效為一個節點載荷進行求解,因此熱應力問題本質上還是一個固體力學問題的有限元求解,而我們剛才提到的傳熱問題的有限元求解其實是在求解傅里葉傳熱偏微分方程,其與固體力學偏微分方程是完全不同的兩套理論。
因此,本文首先重點講解的溫度作用產生的節點等效溫度荷載有限元列式的推導,六面體單元剛度矩陣、雅各比矩陣、應變矩陣有限元列式的推導,溫度應力應變的后處理有限元列式,此外還包括上述有限元列式對應的matlab代碼實現過程。
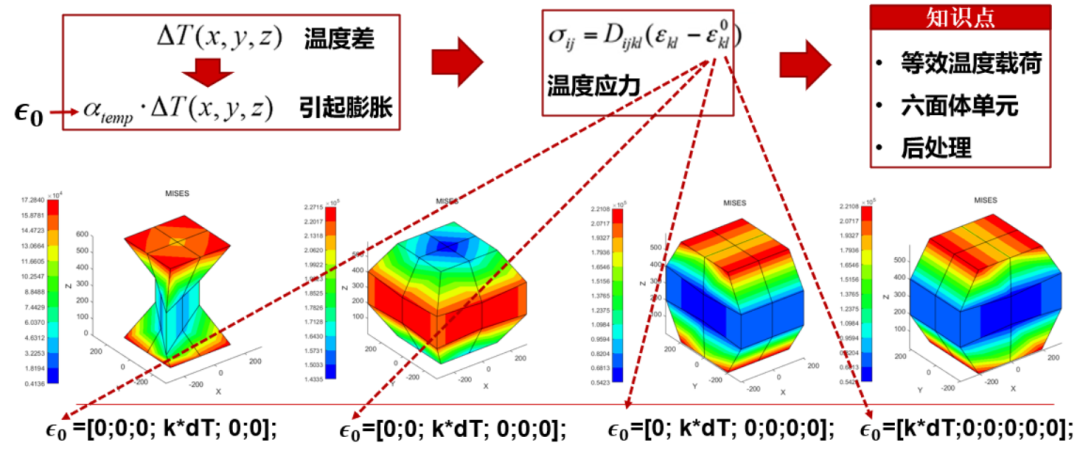
圖1 兩端固定約束的四棱柱受單位熱應變作用下的應力
假定通過傳熱分析我們可以得到,相對于原來狀態溫度升高了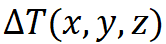 ,對于各向同性材料,溫度升高
,對于各向同性材料,溫度升高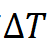 會產生一個均勻的應變(通俗地講,就是熱脹冷縮原理,物體會發生膨脹),應變大小與材料的線膨脹系數
會產生一個均勻的應變(通俗地講,就是熱脹冷縮原理,物體會發生膨脹),應變大小與材料的線膨脹系數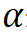 有關,
有關,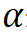 表示材料在單位溫度升高所引起的長度的變化值,一般情況下,在一定范圍內可以假定線膨脹系數為常數。若物體能夠自由變形,則由溫度變化引起的應變不會產生應力。溫度應變一般被表示為初應變的形式
表示材料在單位溫度升高所引起的長度的變化值,一般情況下,在一定范圍內可以假定線膨脹系數為常數。若物體能夠自由變形,則由溫度變化引起的應變不會產生應力。溫度應變一般被表示為初應變的形式
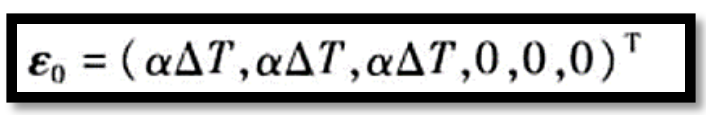 ? ??(1)
? ??(1)
對應的應力-應變關系為
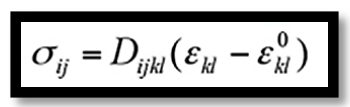 ? ? ? ? (2)
? ? ? ? (2)
接下來將公式(2)的應力應變關系代入到有限元分析列式中,利用虛功原理進行推導。其中虛應力和虛應變場函數的有限元列式如下式
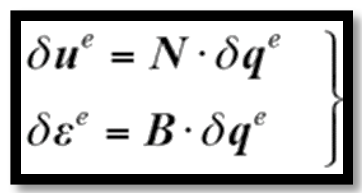 ? ? ? ? ? ?(3)
? ? ? ? ? ?(3)
將公式(2)利用虛功原理,可得到下述虛功方程
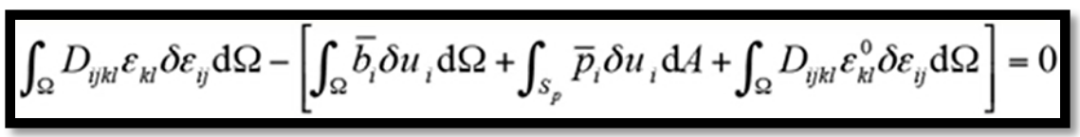 ? ? ? (4)
? ? ? (4)
將公式(3)代入公式(4)所示的虛功方程中,并對其進行簡化處理,可以得到
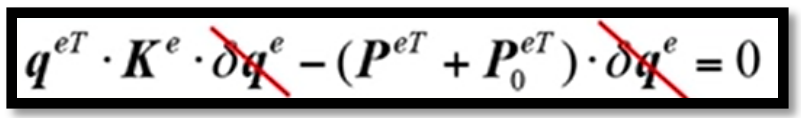 ? ??(5)
? ??(5)
因為虛位移存在任意性,因此可以除掉公式(5)中的虛位移,進而得到
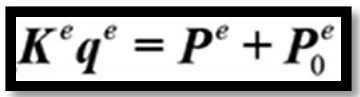 ? ? ?(6)
? ? ?(6)
其中Ke為剛度矩陣,表達式為
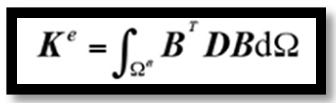 ? ? ? ?(7)
? ? ? ?(7)
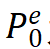 為單元節點載荷,表達式為
為單元節點載荷,表達式為
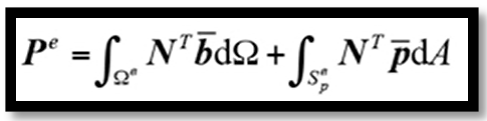 ? ? ??(8)
? ? ??(8)
為等效溫度載荷,是由熱應力引起的節點處等效溫度載荷,表達式為
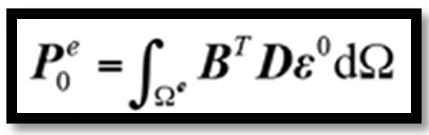 ??? ? ? (9)
??? ? ? (9)
因此,對于溫度應力問題,核心就是求解等效溫度載荷。因為公式中包含了B矩陣,即應變矩陣,對于六面體單元應變矩陣的推導過程如下圖所示。

圖1 應變矩陣與剛度矩陣的推導公式
基于圖1所示的應變矩陣的推導過程,公式(9)中等效溫度載荷對應的matlab代碼如下所示,此外本段代碼同樣包含了單元剛度矩陣的編程實現,因為等效溫度載荷和單元剛度矩陣的求解公式中均有B矩陣和D矩陣參與。
for X=1:2 for Y=1:2 for Z=1:2 GP1=GaussCoordinate(X); GP2=GaussCoordinate(Y); GP3=GaussCoordinate(Z); %高斯點坐標 % 計算形函數對總體坐標的導數(NDerivative)及雅可比矩陣行列式(JacobiDET) [~,NDerivative, JacobiDET] = ShapeFunction([GP1 GP2 GP3], ElementNodeCoordinate); Coefficient=GaussWeight(X)*GaussWeight(Y)*GaussWeight(Z)*JacobiDET; %計算B矩陣 利用形函數對總體坐標的導數(NDerivative)對B進行計算 B=zeros(6,24); for I=1:8 COL=(I-1)*3+1:(I-1)*3+3; B(:,COL)=[NDerivative(1,I) 0 0; 0 NDerivative(2,I) 0; 0 0 NDerivative(3,I); NDerivative(2,I) NDerivative(1,I) 0; 0 NDerivative(3,I) NDerivative(2,I); NDerivative(3,I) 0 NDerivative(1,I)]; end Ke=Ke+Coefficient*B'*D*B; %疊加剛度陣 P_dT=P_dT+Coefficient*B'*D*epsilon0; %等效溫度荷載 end end end
上述代碼中,求解雅各比矩陣行列式和形函數導數的ShapeFunction函數的matlab代碼如下所示:
function [N,NDerivative,JacobiDET] = ShapeFunction(GaussPoint,ElementNodeCoordinate) %等參元坐標 每一列代表一個點的坐標 ParentNodes=[-1 1 1 -1 -1 1 1 -1; -1 -1 1 1 -1 -1 1 1; -1 -1 -1 -1 1 1 1 1]; N=zeros(8,1); %初始化形函數矩陣8*1 ParentNDerivative=zeros(3,8);%初始化形函數對局部坐標的導數矩陣3*8 %計算形函數及形函數對局部坐標導數 for I=1:8 XPoint = ParentNodes(1,I); YPoint = ParentNodes(2,I); ZPoint = ParentNodes(3,I); ShapePart = [1+GaussPoint(1)*XPoint 1+GaussPoint(2)*YPoint 1+GaussPoint(3)*ZPoint]; %定義中間變量 N(I) = 0.125*ShapePart(1)*ShapePart(2)*ShapePart(3); ParentNDerivative(1,I) = 0.125*XPoint*ShapePart(2)*ShapePart(3); ParentNDerivative(2,I) = 0.125*YPoint*ShapePart(1)*ShapePart(3); ParentNDerivative(3,I) = 0.125*ZPoint*ShapePart(1)*ShapePart(2); end Jacobi = ParentNDerivative*ElementNodeCoordinate;%計算雅可比矩陣 JacobiDET = det(Jacobi);%計算雅可比行列式 JacobiINV=inv(Jacobi);%對雅可比行列式求逆 NDerivative=JacobiINV*ParentNDerivative;%利用雅可比行列式的逆計算形函數對結構坐標的導數3*8 end
單元剛度矩陣和等效溫度載荷求得之后,將其裝配到整體剛度矩陣和荷載向量中通過高斯消去法實現節點位移的求解,求解之后的節點位移按照下圖中的后處理流程和對應的公式,即可求解得到高斯積分點處的應力應變值,需要注意的是如公式(2)所示單元應力的求解公式中包含了溫度應變;下一步再通過插值函數矩陣將高斯積分點處的應力應變插值到每個節點再進行磨平處理,即可得到節點的應力應變。具體matlab實現代碼如下所示:
InterpolationMatrix=zeros(8,8);%求解節點應力應變的插值矩陣 %循環高斯點 for X=1:2 for Y=1:2 for Z=1:2 E1=GaussCoordinate(X); E2=GaussCoordinate(Y); E3=GaussCoordinate(Z); GaussPointNumber = GaussPointNumber + 1; % 計算局部坐標下的形函數及形函數導數 [N,NDerivative, ~] = ShapeFunction([E1 E2 E3], ElementNodeCoordinate); ElementNodeDisplacement=U(ElementNodeDOF); ElementNodeDisplacement=reshape(ElementNodeDisplacement,Dof,8); % 計算高斯點應變 GausspointStrain3_3 3*3的應變矩陣 GausspointStrain3_3=ElementNodeDisplacement*NDerivative’;%3*8 8*3 %把高斯點應變矩陣改寫成6*1 GausspointStrain=[GausspointStrain3_3(1,1) GausspointStrain3_3(2,2) GausspointStrain3_3(3,3)… GausspointStrain3_3(1,2)+GausspointStrain3_3(2,1)… GausspointStrain3_3(2,3)+GausspointStrain3_3(3,2) … GausspointStrain3_3(1,3)+GausspointStrain3_3(3,1)]'; % 計算高斯點應力 GausspointStress = D*GausspointStrain-D*epsilon0;%總應變-溫度應變 GaussStrain(:,GaussPointNumber)=GausspointStrain; GaussStress(:,GaussPointNumber)=GausspointStress; InterpolationMatrix(K,:)=N; K=K+1; end end end %求得節點應力應變 Temp1=InterpolationMatrix(GaussStrain(1:6,GaussPointNumber-7:GaussPointNumber)'); NodeStrain(1:6,INODE+1:INODE+8)=Temp1'; Temp2=InterpolationMatrix(GaussStress(1:6,GaussPointNumber-7:GaussPointNumber)'); NodeStress(1:6,INODE+1:INODE+8)=Temp2';
上述便是熱應力問題的整個求解過程,以一個兩端固定約束的四棱柱為例,其在不同單位熱應變的作用下的求解結果如下圖所示
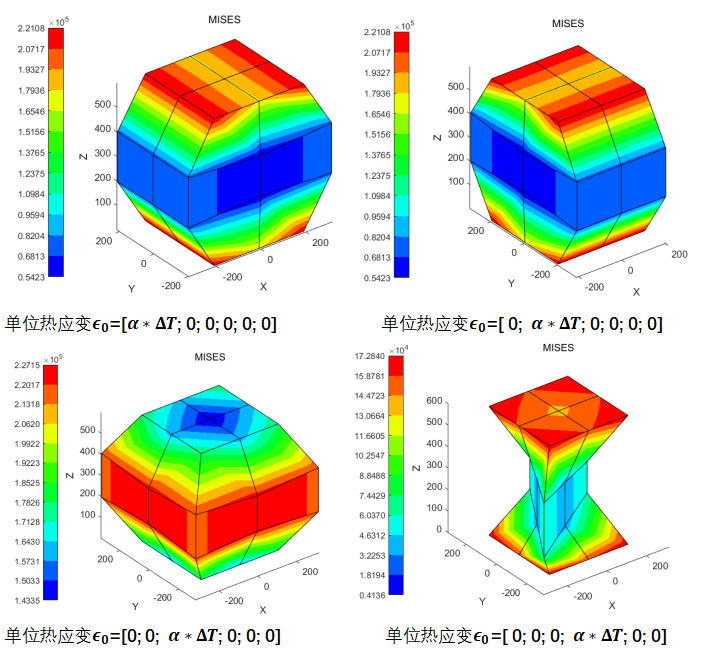
以上就是筆者本期要分享的內容。
-
matlab
+關注
關注
189文章
3001瀏覽量
234211 -
編程
+關注
關注
88文章
3689瀏覽量
95285 -
熱應力
+關注
關注
0文章
11瀏覽量
10845
原文標題:基于六面體單元熱應力問題的Matlab有限元編程求解
文章出處:【微信號:sim_ol,微信公眾號:模擬在線】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
六相感應電機轉子感應電壓有限元分析與研究
MATLAB有限元分析與應用
封裝中的界面熱應力分析
有限元仿真分析軟件的三種算法模型格式介紹
有限元法的原理
OptiMode:矢量有限元法-精度及優勢
不可壓縮Navier-Stokes方程并行譜有限元法求解

n型結構膜盤聯軸器型面設計與有限元分析
六面體網格生成和優化的研究綜述

六面體網格復雜層插入操作的優化設計






 基于六面體單元熱應力問題的Matlab有限元編程求解
基于六面體單元熱應力問題的Matlab有限元編程求解











評論