導(dǎo)讀:大家好,我是SimPC博士,主要從事工程結(jié)構(gòu)抗震及減隔震研究,玻璃成型熱工設(shè)備流動(dòng)及傳熱研究,玻璃材料力學(xué)性能研究。精通有限元等數(shù)值算法的實(shí)現(xiàn),有限元軟件二次開(kāi)發(fā),數(shù)據(jù)處理,偏微分方程求解,優(yōu)化算法,GUI界面開(kāi)發(fā)等。有多項(xiàng)科研成果,其中SCI論文4篇,EI3篇,專利2篇。
近日我注冊(cè)并認(rèn)證了仿真秀專欄,將在仿真秀官網(wǎng)和App給平臺(tái)用戶帶來(lái)Matlab有限元編程、復(fù)雜函數(shù)擬合和matlab繪圖相關(guān)內(nèi)容。此外還會(huì)帶來(lái)隔震建筑Abaqus建模仿真分析等內(nèi)容。本次案例主要以受均布荷載和集中荷載的變截面懸臂梁為研究對(duì)象,通過(guò)matlab編制四節(jié)點(diǎn)和八節(jié)點(diǎn)四邊形單元有限元程序來(lái)對(duì)懸臂梁進(jìn)行受力分析。
一、問(wèn)題概述
如圖1-1 所示,某變截面懸臂梁長(zhǎng)度為2m,截面面積由0.6m至0.2m線性變化,受作用在自由端節(jié)點(diǎn)的集中荷載2P=kN和豎直方向均布荷載q=1kN/m作用,按平面應(yīng)力問(wèn)題分析,求解自由端節(jié)點(diǎn)撓度。變截面懸臂梁采用C30混凝土,彈性模量為E= 4 3 10 MPa,泊松比為。編制四節(jié)點(diǎn)和八節(jié)點(diǎn)四邊形單元有限元程序,最終得到梁的變形。
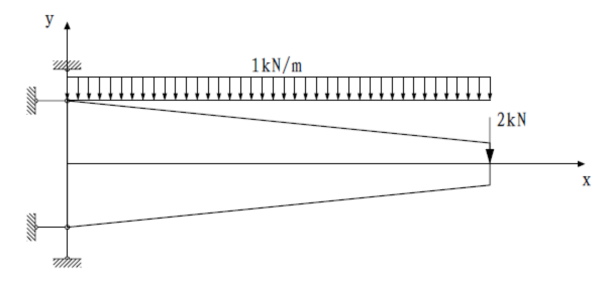
圖1-1 變截面懸臂梁
二、求解思路
對(duì)于本問(wèn)題采用基于MATLAB 編制有限元分析程序進(jìn)行求解,其基本組成部分包括前處理模塊、分析主程序模塊和后處理模塊。在前處理模塊中,實(shí)現(xiàn)節(jié)點(diǎn)坐標(biāo)輸入、單元節(jié)點(diǎn)編號(hào)、網(wǎng)絡(luò)劃分以及邊界條件輸入等工作;在分析主程序模塊中,求解整體剛度方程;在后處理模塊中,實(shí)現(xiàn)結(jié)果顯示、數(shù)據(jù)輸出等工作。本文主要針對(duì)四節(jié)點(diǎn)四邊形單元與八節(jié)點(diǎn)四邊形單元理論和對(duì)應(yīng)的計(jì)算程序進(jìn)行講解。
有限元法的基本步驟:
-
幾何域離散,獲得標(biāo)準(zhǔn)化的單元;
-
通過(guò)能量原理(虛功原理或最小勢(shì)能原理,獲得單元?jiǎng)偠确匠蹋?/span>
-
單元的集成(裝配);
-
處理位移邊界條件;
-
計(jì)算支反力;
- 計(jì)算單元的其他物理量(應(yīng)力應(yīng)變)。
-
節(jié)點(diǎn)描述
-
場(chǎng)描述
- 單元?jiǎng)偠确匠獭?/span>
1、平面問(wèn)題的平衡方程、幾何方程、物理方程
平面問(wèn)題的彈性力學(xué)基礎(chǔ)理論是推導(dǎo)有限元方程的基礎(chǔ),所以先羅列出平面問(wèn)題的平衡方程、幾何方程、物理方程,具體如公式(1)-(3)所示。至于這些方程的推導(dǎo)過(guò)程大家可以參考任意彈性力學(xué)課本,都會(huì)進(jìn)行詳細(xì)的講解。
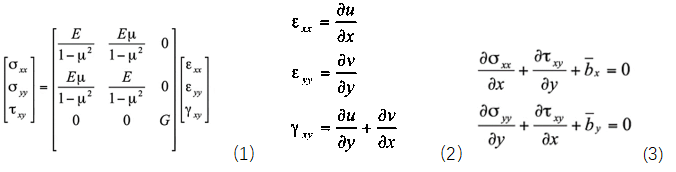
2、等參單元
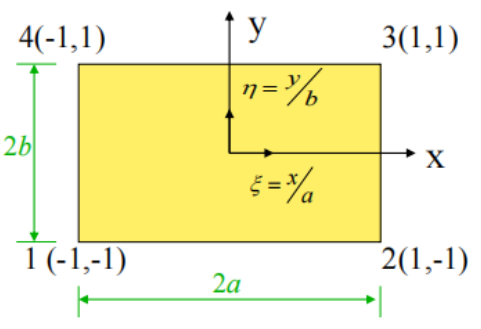
在有限元方法中,若要離散邊界為曲線或曲面的求解域,需要建立將形狀規(guī)則的單元變換為邊界為曲線或曲面的單元的方法,在有限元法中對(duì)應(yīng)此問(wèn)題所采用的變換方法是等參變換,即單元幾何形狀的變換和單元內(nèi)長(zhǎng)函數(shù)采用相同數(shù)目的節(jié)點(diǎn)及相同的插值函數(shù)進(jìn)行變換。同樣我們今天要講的四邊形單元也從其對(duì)應(yīng)的等參單元的基礎(chǔ)理論講起。四邊形單元可以由自然坐標(biāo)系中的矩形單元映射而成,映射關(guān)系如圖2-1所示。
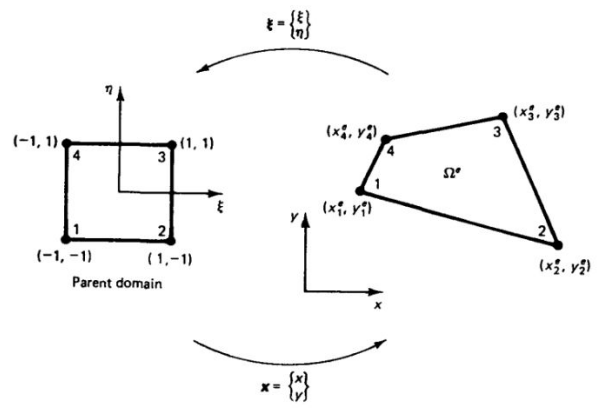
圖2-1 平面四節(jié)點(diǎn)矩形單元的映射關(guān)系
在自然坐標(biāo)系下,矩形單元是規(guī)則化的,當(dāng)自然坐標(biāo)系中的單元取為雙線性單元時(shí)(也即為四節(jié)點(diǎn)四邊形單元),平面四節(jié)點(diǎn)矩形單元如圖2-2所示,單元有4個(gè)節(jié)點(diǎn),8個(gè)自由度。單元的形函數(shù)定義如下: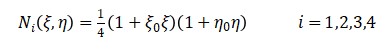 ? ? ?
? ? ?(4)其中,
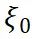 和
和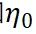 為自然坐標(biāo)系下的節(jié)點(diǎn)坐標(biāo)值。單元從自然坐標(biāo)系到物理坐標(biāo)系的映射為
為自然坐標(biāo)系下的節(jié)點(diǎn)坐標(biāo)值。單元從自然坐標(biāo)系到物理坐標(biāo)系的映射為

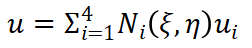 ? ? ? ? ? ? ? ? ? ?(7)
? ? ? ? ? ? ? ? ? ?(7)
function N=ShapeFun(s,t)N1=1/4*(1-s)*(1-t);N2=1/4*(1+s)*(1-t);N3=1/4*(1+s)*(1+t);N4=1/4*(1-s)*(1+t);N=[N1 0 N2 0 N3 0 N4 0;0 N1 0 N2 0 N3 0 N4];end
同理平面八節(jié)點(diǎn)矩形單元如圖2-3所示,單元共有8個(gè)節(jié)點(diǎn),16個(gè)自由度。單元的形函數(shù)定義如下:
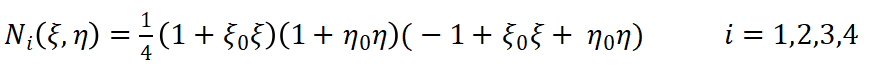 ? (8)
? (8)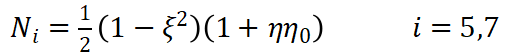 ? ? ? ?(9)
? ? ? ?(9)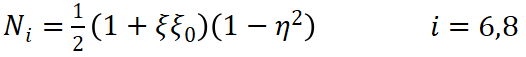 ? (10)
? (10)其中,
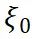 和
和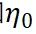 為自然坐標(biāo)系下的節(jié)點(diǎn)坐標(biāo)值。單元從自然坐標(biāo)系到物理坐標(biāo)系的映射為
為自然坐標(biāo)系下的節(jié)點(diǎn)坐標(biāo)值。單元從自然坐標(biāo)系到物理坐標(biāo)系的映射為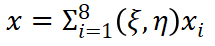 ? ? ?(11)
? ? ?(11)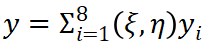 ? ? ? ?(12)
? ? ? ?(12)在進(jìn)行映射變換時(shí)候,要求單元兩個(gè)坐標(biāo)系下的節(jié)點(diǎn)編號(hào)要對(duì)應(yīng)。單元的節(jié)點(diǎn)變量用型函數(shù)進(jìn)行插值,有
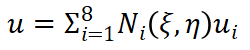 ?? (13)
?? (13)
function N=ShapeFun(s,t)%% 四邊形八結(jié)點(diǎn)等參單元形函數(shù)矩陣% 角點(diǎn)N1=1/4*(1-s)*(1+t)*(-s+t-1);N2=1/4*(1-s)*(1-t)*(-s-t-1);N3=1/4*(1+s)*(1-t)*(s-t-1);N4=1/4*(1+s)*(1+t)*(s+t-1);% 邊中點(diǎn)N5=1/2*(1-t^2)*(1-s);N7=1/2*(1-t^2)*(1+s);N6=1/2*(1-s^2)*(1-t);N8=1/2*(1-s^2)*(1+t);N=[N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8 0;0 N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8];
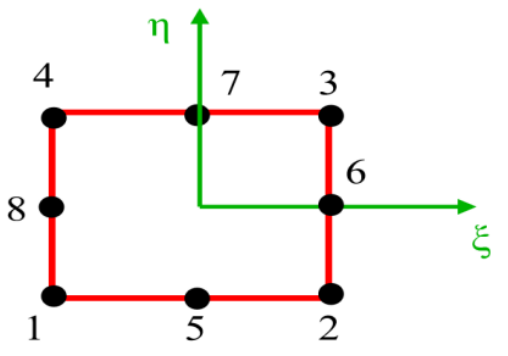
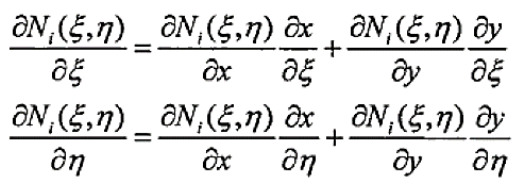 (14)
(14)寫(xiě)成矩陣的形式就是
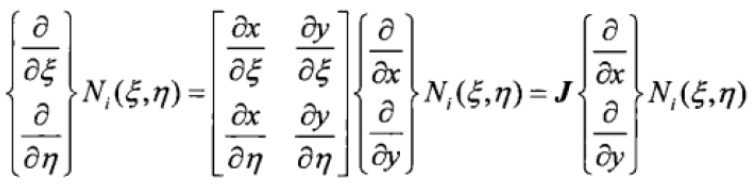 ? ???(15)
? ???(15)其中,J被稱為Jacobi矩陣。反過(guò)來(lái),形函數(shù)對(duì)物理坐標(biāo)的導(dǎo)數(shù)為
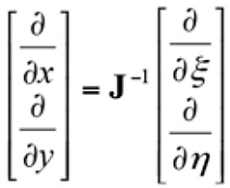 ? ? ? ? ?(16)
? ? ? ? ?(16)另外,對(duì)于二維平面單元還要完成面積的映射,為
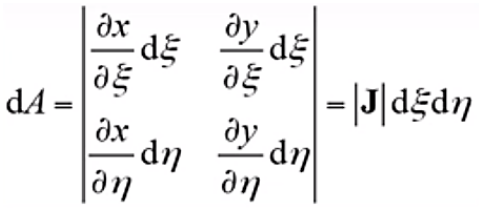 ? ? ? ? ? ? ?(17)
? ? ? ? ? ? ?(17)可以看出Jacob矩陣在等參變化中扮演著至關(guān)重要的角色,Jacob矩陣具體的表達(dá)式如下所示,
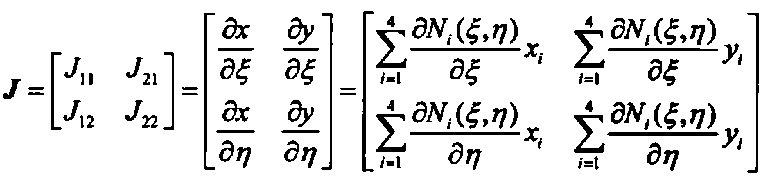 ? ? ? (18)
? ? ? (18)公式18對(duì)應(yīng)的八節(jié)點(diǎn)單元雅各比矩陣的求解代碼為:
公式18對(duì)應(yīng)的四節(jié)點(diǎn)單元雅各比矩陣的求解代碼為:function J=Jacobi(ie,s,t,Elements,Nodes)ENodes = Elements(ie,:); %獲取單元結(jié)點(diǎn)xe = Nodes(ENodes(:),:); %獲取節(jié)點(diǎn)坐標(biāo)x1=xe(1,1);y1=xe(1,2);x2=xe(2,1);y2=xe(2,2);x3=xe(3,1);y3=xe(3,2);x4=xe(4,1);y4=xe(4,2);J=1/4*[-(1+t) -(1-t) 1-t 1+t;1-s -(1-s) -(1+s) 1+s]*[x1 y1;x2 y2;x3 y3;x4 y4];end
3、剛度矩陣的推導(dǎo)function J=Jacobi(ie,kesi,yita,Elements,Nodes)ENodes = Elements(ie,:); %獲取單元結(jié)點(diǎn)xe = Nodes(ENodes(:),:); %獲取結(jié)點(diǎn)坐標(biāo)x1=xe(1,1);y1=xe(1,2);x2=xe(2,1);y2=xe(2,2);x3=xe(3,1);y3=xe(3,2);x4=xe(4,1);y4=xe(4,2);J=1/4*[-(1-yita),(1-yita),(1+yita),-(1+yita);-(1-kesi),-(1+kesi),(1+kesi),(1-kesi)]*[x1 y1;x2 y2;x3 y3;x4 y4];end
為了求出上述平面四節(jié)點(diǎn)和八節(jié)點(diǎn)單元的單元?jiǎng)偠染仃嚕枰柚芰吭恚ㄌ摴υ怼⒆钚?shì)能原理)進(jìn)行推導(dǎo),能量原理的推導(dǎo)過(guò)程大家可以參考任意一本有限元理論書(shū)籍,都會(huì)有詳細(xì)的推導(dǎo)過(guò)程,這里就不做進(jìn)一步推導(dǎo)講解,直接給出物理坐標(biāo)和幾何坐標(biāo)系下的剛度矩陣的公式
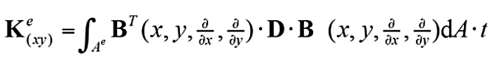 ? ?(19)
? ?(19)
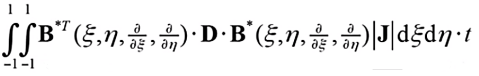 ? ?(20)
? ?(20)
其中B矩陣為應(yīng)變矩陣,如下式;D矩陣為材料剛度矩陣,如公式(1)所示,是物理方程中表征應(yīng)力應(yīng)變關(guān)系的矩陣。從上述剛度矩陣的表達(dá)式可以看出,自然坐標(biāo)和物理坐標(biāo)間要完成坐標(biāo)映射、偏導(dǎo)映射、面積隱射三個(gè)部分,具體映射公式已在上一節(jié)的等參單元講解中詳細(xì)給出。
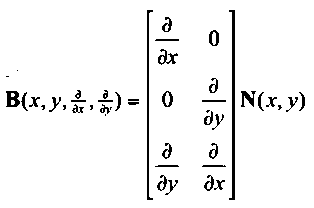 ? ? ? ?(21)
? ? ? ?(21)
4、高斯積分
公式(20)中的單元?jiǎng)偠染仃囃ㄟ^(guò)數(shù)值積分求得,本案例中的四節(jié)點(diǎn)和八節(jié)點(diǎn)四邊形等參單元均采用2*2個(gè)積分點(diǎn)的高斯積分即可求得精確結(jié)果。高斯積分點(diǎn)的坐標(biāo)具體如圖所示。
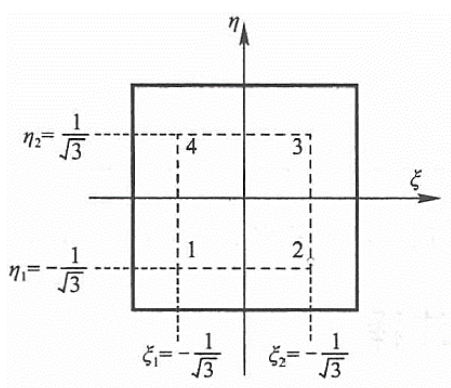
4-1 Gauss積分點(diǎn)示意圖
公式(20)寫(xiě)成數(shù)值積分的形式為
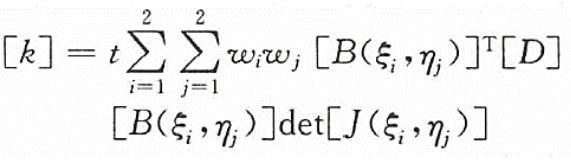 ? ? ? ? (22)
? ? ? ? (22)
對(duì)于8節(jié)點(diǎn)單元實(shí)現(xiàn)上述數(shù)值積分的代碼如下所示:
r = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯積分點(diǎn)s = [r(1) r(1) r(2) r(2)];t = [r(2) r(1) r(1) r(2)]; % 高斯積分點(diǎn)坐標(biāo)for i=1:4J = Jacobi(E_ID,s(i),t(i),Elements,Nodes); % 雅可比矩陣Nst = DiffShapeFun(s(i),t(i)); % 形函數(shù)關(guān)于自然坐標(biāo)s,t求導(dǎo)Nxy = zeros(8,2);for j=1:8:) = (JNst(j,:)')'; % 形函數(shù)關(guān)于 x,y 求導(dǎo)=inv(J)*NstendBm = [Nxy(1,1) 0 Nxy(2,1) 0 Nxy(3,1) 0 Nxy(4,1) 0 Nxy(5,1) 0 Nxy(6,1) 0 Nxy(7,1) 0 Nxy(8,1) 0;0 Nxy(1,2) 0 Nxy(2,2) 0 Nxy(3,2) 0 Nxy(4,2) 0 Nxy(5,2) 0 Nxy(6,2) 0 Nxy(7,2) 0 Nxy(8,2);Nxy(1,1) Nxy(2,2) Nxy(2,1) Nxy(3,2) Nxy(3,1) Nxy(4,2) Nxy(4,1) Nxy(5,2) Nxy(5,1) Nxy(6,2) Nxy(6,1) Nxy(7,2) Nxy(7,1) Nxy(8,2) Nxy(8,1)];ke = ke+det(J)*Bm'*D*Bm*Width; %數(shù)值積分end
5、均布荷載的施加
在有限元中分布力要轉(zhuǎn)為等效節(jié)點(diǎn)荷載,而確定等效節(jié)點(diǎn)荷載的方法也是通過(guò)能量原理推導(dǎo)得到
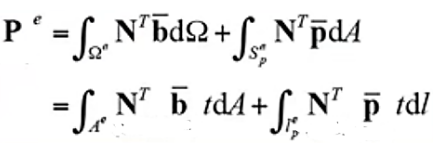 ? ? ? ?(22)
? ? ? ?(22)
上式中,第一項(xiàng)代表體積力的等效荷載,第二項(xiàng)代表面積力的等效荷載,這個(gè)案例我們只考慮面力荷載。實(shí)現(xiàn)公式22的代碼為
function Pe=UniLoad(ie,N_ID_p1,q0,Nodes,Elements)k=-0.625e-3; % 均布荷載值 N/mms = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯積分點(diǎn)ENodes = N_ID_p1(ie,:); %獲取單元結(jié)點(diǎn)號(hào)Pe=zeros(16,1); %生成臨時(shí)單元節(jié)點(diǎn)力零列向量x1=Nodes(ENodes(1),1);x6=Nodes(ENodes(4),1);L16=abs(x6-x1); %單元長(zhǎng)度for i=1:2 %用于高斯積分的求和循環(huán)N_q=ShapeFun(s(i),1); % 4級(jí)子程序:ShapeFun(s(i),1)q_x=q0;Pe=Pe+N_q'*q_x*[0;L16/2];endend
三、Matlab有限元編程精品課
網(wǎng)格劃分及變形結(jié)果如圖3-1所示。本案例的詳細(xì)視頻教程和對(duì)應(yīng)的matlab源碼,請(qǐng)關(guān)注我的仿真秀官網(wǎng)和APP精品課程《Matlab有限元編程從入門(mén)到精通10講》。

圖3-1 梁變形結(jié)果
-
matlab
+關(guān)注
關(guān)注
189文章
3001瀏覽量
234090 -
編程
+關(guān)注
關(guān)注
88文章
3689瀏覽量
95231
原文標(biāo)題:教你Matlab有限元編程對(duì)懸臂梁進(jìn)行受力分析-附源碼及教程
文章出處:【微信號(hào):sim_ol,微信公眾號(hào):模擬在線】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
MATLAB有限元分析與應(yīng)用
懸臂梁式傳感器的原理是什么?
利用微電鑄制作鎳懸臂梁
靜電式微開(kāi)關(guān)硅懸臂梁的變形分析
雙孔懸臂梁應(yīng)變傳感器—稱重實(shí)驗(yàn)

基于comsol的懸臂梁形變實(shí)驗(yàn)報(bào)告
采用環(huán)梁加固風(fēng)機(jī)基礎(chǔ)的有限元分析
測(cè)量?jī)x懸臂梁拓?fù)鋬?yōu)化
華盛頓大學(xué)利用懸臂梁開(kāi)發(fā)出激光制冷新技術(shù)
懸臂梁稱重傳感器的工作原理
基于箱形梁CADCAE有限元分析

基于六面體單元熱應(yīng)力問(wèn)題的Matlab有限元編程求解
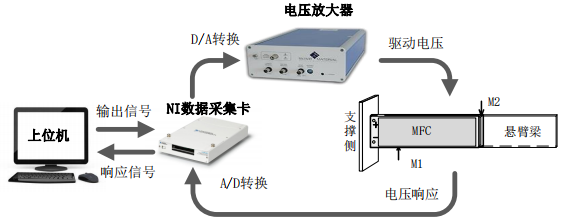
電壓放大器在自感知的懸臂梁變形控制研究中的應(yīng)用





 基于Matlab有限元編程的變截面懸臂梁分析
基于Matlab有限元編程的變截面懸臂梁分析











評(píng)論