木材表面缺陷不利于木材的加工利用,降低木制品的品質(zhì),影響生產(chǎn)企業(yè)的經(jīng)濟(jì)效益,因此木材表面缺陷的圖像檢測(cè)技術(shù)越來(lái)越受重視。而采用圖像處理方法進(jìn)行木材表面缺陷檢測(cè),是實(shí)現(xiàn)木材表面缺陷自動(dòng)檢測(cè)、提高企業(yè)生產(chǎn)效率的必由之路。
鑒于圖割方法的明顯優(yōu)勢(shì),白雪冰及其團(tuán)隊(duì)采用Graph Cuts算法和Grab Cut算法分別對(duì)木材表面的單目標(biāo)和多目標(biāo)缺陷圖像進(jìn)行分割試驗(yàn),以總結(jié)傳統(tǒng)圖割方法的不足和改進(jìn)算法的優(yōu)點(diǎn)。
針對(duì)傳統(tǒng)Graph Cuts算法只能針對(duì)灰度圖像進(jìn)行分割、運(yùn)行時(shí)參數(shù)的選擇比較復(fù)雜,并且存在該算法效率和精度較低的缺陷,采用這兩種方法分別對(duì)3種木材表面缺陷活節(jié)、蟲(chóng)眼和死節(jié)圖像進(jìn)行分割實(shí)驗(yàn)。為了驗(yàn)證Grab Cuts方法的適用性,用含有多個(gè)缺陷目標(biāo)的木質(zhì)板材圖像做了圖像分割驗(yàn)證。
結(jié)果表明:缺陷圖像的目標(biāo)和背景的種子點(diǎn)選取直接影響Graph Cuts算法的分割結(jié)果,Graph Cuts算法的計(jì)算效率較低,分割時(shí)間較長(zhǎng),對(duì)相鄰像素間的區(qū)分度較差,分割結(jié)果不理想。改進(jìn)后的Grab Cut算法是迭代的Graph Cuts,該方法雖然在圖像分割前也需要人工畫(huà)定初始化矩形框,但操作相對(duì)簡(jiǎn)單,分割結(jié)果能夠得到完整的閉合缺陷區(qū)域邊界,且不受木材表面缺陷的類(lèi)型、數(shù)量、尺寸和缺陷形狀的影響,分割效果好,分割速度快,抗噪性強(qiáng),對(duì)灰度圖像和彩色圖像都可使用。
1、圖割算法
1.1Graph Cuts 算法的原理
圖割(Graph Cuts)交互式圖像分割算法是一種基于圖論的組合最優(yōu)化方法,其基礎(chǔ)是最大流算法,將圖像分割問(wèn)題轉(zhuǎn)化成能量函數(shù)的最小化問(wèn)題,通過(guò)最小化能量函數(shù),從而實(shí)現(xiàn)圖像的最優(yōu)分割。首先,建立能量函數(shù):
E(L) =R(L) +λB(L) (1)
式中:R(L)是區(qū)域項(xiàng),表示區(qū)域?qū)傩裕籅(L)是邊界項(xiàng),表示邊界屬性;λ 為平衡因子,當(dāng)λ 較小時(shí),邊界項(xiàng)可忽略,當(dāng)λ 較大時(shí),圖像的所有點(diǎn)被賦予相同標(biāo)記。
設(shè)P={p1,p22,…,pN2} 是像素集合,L={0,1}是像素標(biāo)記集合,0表示背景,1表示目標(biāo);像素的標(biāo)記可以表示為從P到L的映射, 記作fp={fp|fp∈L}。
因此,式(1)中的區(qū)域項(xiàng)表示為R(f)=Rp(fp),p∈P,用Rp(fp)來(lái)進(jìn)行判定像素p分配給某種標(biāo)記的可能性。通常對(duì)能量函數(shù)中的區(qū)域項(xiàng)取概率的負(fù)對(duì)數(shù),且將預(yù)定義的種子點(diǎn)作為目標(biāo)和背景的采樣,以此估計(jì)目標(biāo)和背景的灰度直方圖分布,對(duì)于目標(biāo)/背景的二值分割,區(qū)域項(xiàng)可表示為:
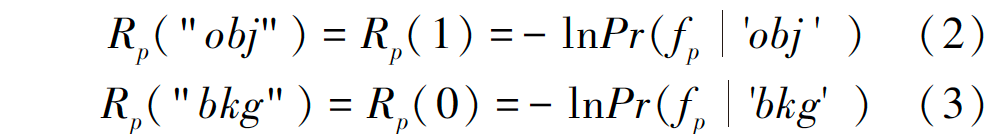
式(2)代表了像素p分配給目標(biāo)區(qū)域的可能性,式(3)代表像素p分配給背景區(qū)域的可能性,隨著可能性的增大,Rp(?) 的值會(huì)減小,從而可通過(guò)最小化能量函數(shù)來(lái)實(shí)現(xiàn)對(duì)圖像的準(zhǔn)確分割。式(1)的邊界項(xiàng)可表示為:
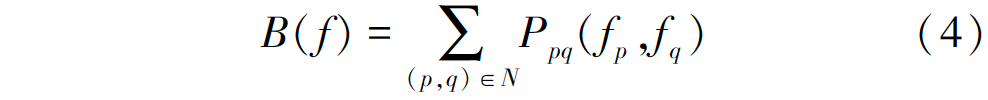
式中:p和q為相鄰像素,邊界項(xiàng)體現(xiàn)圖像邊界像素值的不連續(xù)性;N為4鄰域或8鄰域系統(tǒng)。通過(guò)變分模型可以將式(4)寫(xiě)為:
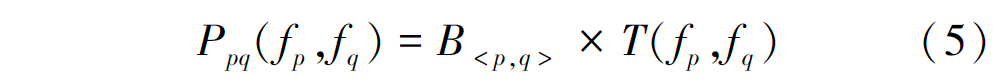
其中, T(fp,fq) 為指標(biāo)函數(shù),滿(mǎn)足 :
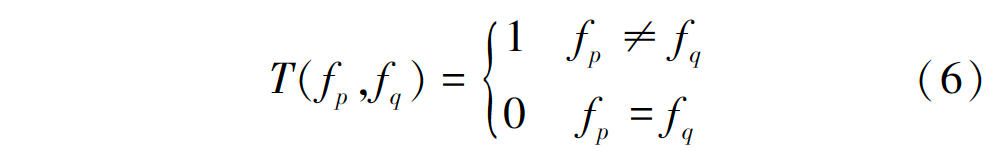
B 為對(duì)像素p、q不連續(xù)性的懲罰值:
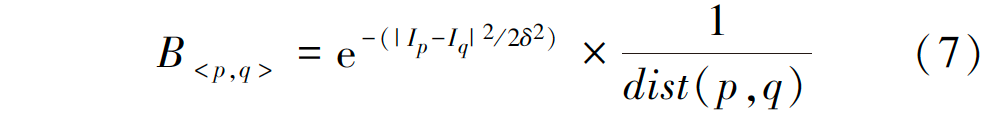
式中:Ip、Iq為像素p、q的灰度值;dist(p,q)是p和q的距離;δ為圖像噪聲。p和q越相近,則B越大;若p和q相差較大,則B趨近于0 。當(dāng)B的值較小時(shí),兩個(gè)像素會(huì)更易于分給不同的區(qū)域,這時(shí)圖像分割得到最小的能量值。
Graph Cuts算法源于圖論,通過(guò)最小化能量函數(shù)實(shí)現(xiàn)圖像分割 。首先要對(duì)(1)的能量函數(shù)公式來(lái)構(gòu)造網(wǎng)絡(luò)圖,把表示帶有非負(fù)邊權(quán)的無(wú)向圖G= (V,E)作為圖像,其中V為頂點(diǎn)集,與其相對(duì)應(yīng)圖像的邊集為像素點(diǎn)集P,E。V含有兩個(gè)特殊的頂點(diǎn),其一稱(chēng)為源節(jié)點(diǎn)S(代表目標(biāo)),其二稱(chēng)為匯節(jié)點(diǎn)T(代表背景),因此構(gòu)造的網(wǎng)絡(luò)圖又稱(chēng)為S-T圖。
1956年Ford等提出了網(wǎng)絡(luò)流理論,論證了網(wǎng)絡(luò)圖中的最大流與最小流的等價(jià)性。式(1)的能量函數(shù)可通過(guò)最大流/最小割定理來(lái)求解,具體包括增廣路徑(augmenting paths)法和推進(jìn)?重標(biāo)記(push-relabel)法。本試驗(yàn)采用后者。
1.2Graph Cut算法的原理
由于Graph Cuts算法只能分割灰度圖像,且參數(shù)選擇復(fù)雜,效率和分割精度較低。因此,Blake等從以下三方面進(jìn)行了改進(jìn),形成Grab Cut算法 :
1)棄用灰度直方圖,轉(zhuǎn)而選用高斯混合模型(GMM 模型)來(lái)描述顏色信息的概率分布,實(shí)現(xiàn)彩色圖像分割;
2)在GMM模型參數(shù)估計(jì)過(guò)程中,采用可進(jìn)化的迭代算法取代一次最小估計(jì)來(lái)完成能量最小化,提高了分割精度;
3)為了降低用戶(hù)交互的工作量,通過(guò)非完全標(biāo)號(hào)(incomplete labeling)方式(交互中沒(méi)有指定明確的目標(biāo))進(jìn)行像素標(biāo)記。該方法只需用戶(hù)在目標(biāo)周?chē)?huà)一個(gè)矩形框即可。
Grab Cut算法把圖像表示為矢量Z= {z1,z2,…,zn,…,zN} ,這樣便將圖像的分割轉(zhuǎn)化為求每個(gè)像素對(duì)應(yīng)的不透明度數(shù)組α= {α1,α2,…,αn,…,αN}αN|(αn∈[0,1]),αn取值為0(背景)或者1(目標(biāo)),圖像目標(biāo)與背景模型分別用k維的全協(xié)方差矩陣GMM表達(dá),通常k=5。向量k={k1,k2,…,kn,…,kN}為每個(gè)像素的獨(dú)立GMM(目標(biāo)或背景的參數(shù),參數(shù)來(lái)自目標(biāo)還是背景,取決于αn的值 ,從而使目標(biāo)提取問(wèn)題轉(zhuǎn)化為能量函數(shù)的最優(yōu)化問(wèn)題,然后采用圖割方法求解。
對(duì)于RGB空間上的彩色圖像,吉布斯(Gibbs)能量函數(shù)為:
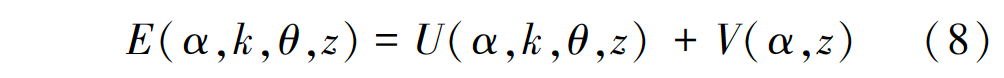
式中:E為能量;U代表數(shù)據(jù)項(xiàng);V代表光滑項(xiàng);α代表不透明度;θ代表圖像目標(biāo)和背景的灰度直方圖;z代表圖像灰度值數(shù)值。數(shù)據(jù)項(xiàng)U定義為:
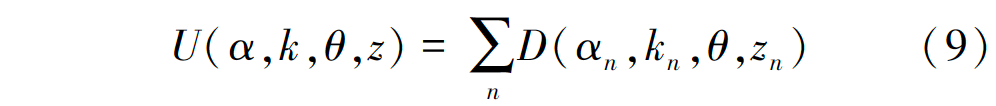
其中, D(αn,kn,θ,zn) = -logp(zn|αn,kn,θ)-
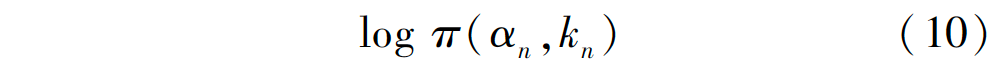
式中:π(?) 代表該高斯模型的樣本數(shù)在總樣本中的混合權(quán)重系數(shù);p(?)代表高斯概率分布。所以數(shù)據(jù)項(xiàng)又可表示為:
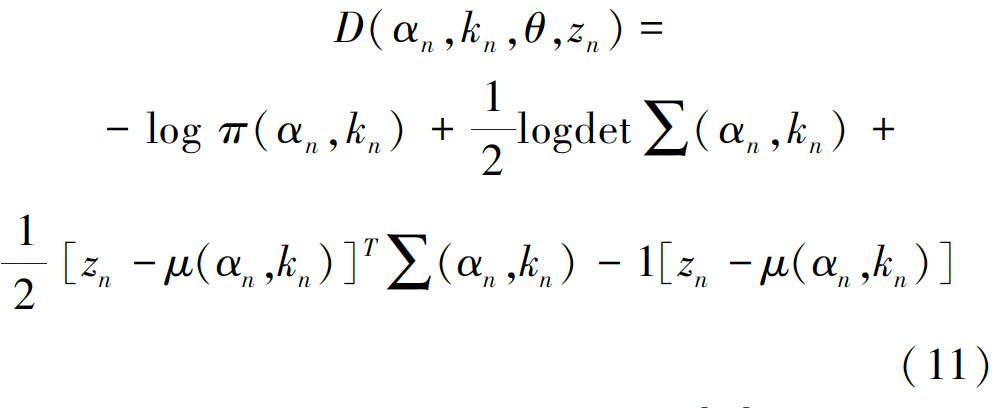
則高斯混合模型的參數(shù)模型為:

其中:π(α,k)代表每個(gè)高斯概率分布的樣本數(shù)在總樣本數(shù)中的權(quán)值;μ(α,k) 代表高斯模型的均值;
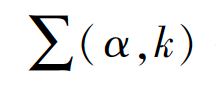
代表協(xié)方差;α代表不透明度Alpha值;k代表高斯混合模型參數(shù)。
平滑項(xiàng)V可以采用RGB彩色空間的歐幾里德距離求得:
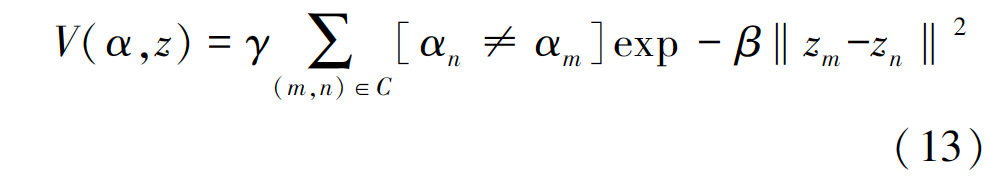
式中:C代表相鄰像素對(duì);γ為自適應(yīng)λ參數(shù);β為常數(shù)項(xiàng)。
若把一個(gè)更接近真實(shí)情況的標(biāo)記賦予某個(gè)像素,則將會(huì)懲罰更小的數(shù)據(jù)項(xiàng),這樣會(huì)使總能量函數(shù)減少,不斷地迭代,最終收斂至最優(yōu)分割,這樣便將Grab Cut算法的圖像分割問(wèn)題轉(zhuǎn)化成求解最小割的問(wèn)題。
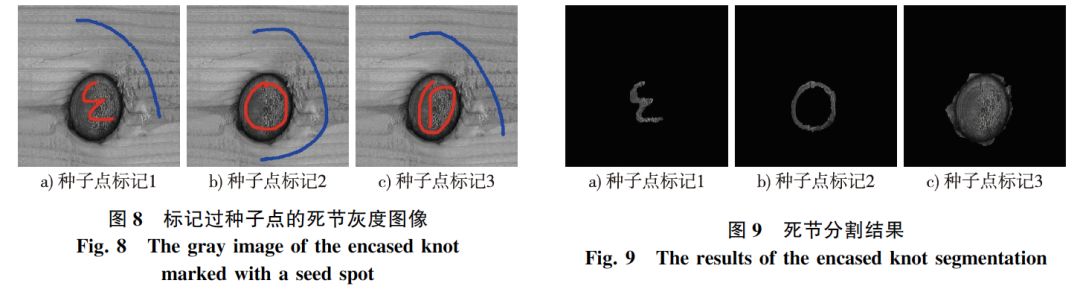
Grab Cut算法的圖像分割步驟如圖1所示。
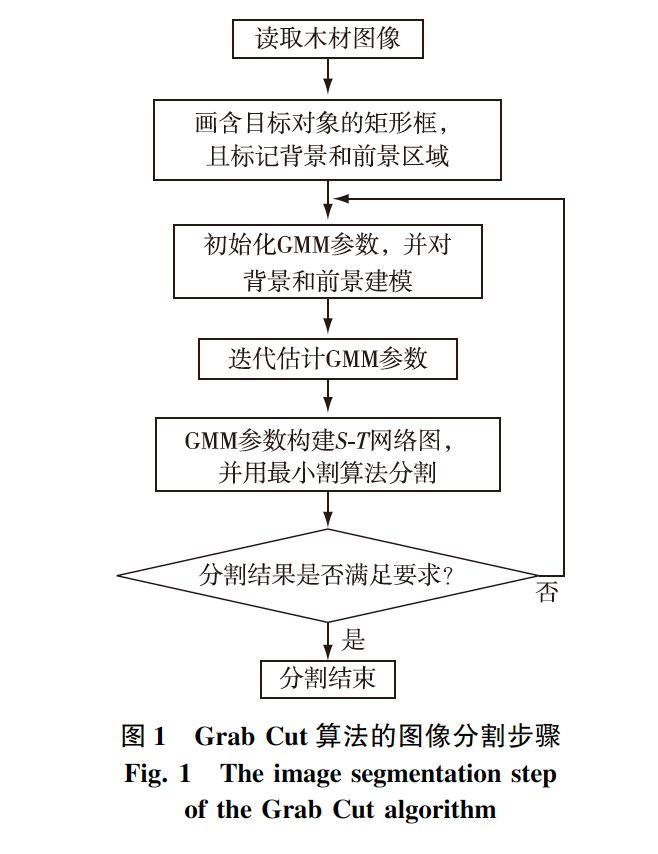
2、木材表面缺陷圖像分割試驗(yàn)
2.1基于Graph Cuts算法的木材表面缺陷圖像分割
本試驗(yàn)采用的計(jì)算機(jī)為Intel(R) Core(TM)i5-4200U CPU,1.60G硬盤(pán),4G RAM,操作系統(tǒng)為Windows 7 with SP1,編程軟件為Visual Studio 2010 C++,OpenCV庫(kù)。
采用Graph Cuts算法對(duì)單缺陷目標(biāo)圖像進(jìn)行圖像分割,木材樣本如圖2,灰度圖像如圖3。
2.1.1活節(jié)缺陷的圖像分割
采用Graph Cuts算法對(duì)圖3a活節(jié)缺陷圖像進(jìn)行分割,參數(shù)λ=1。試驗(yàn)中對(duì)活節(jié)灰度圖像進(jìn)行3次人工種子點(diǎn)標(biāo)記(其中紅色為目標(biāo)標(biāo)記,藍(lán)色為背景標(biāo)記,且標(biāo)記畫(huà)筆的半徑是5個(gè)像素),如圖4所示,對(duì)應(yīng)的分割結(jié)果如圖5所示。
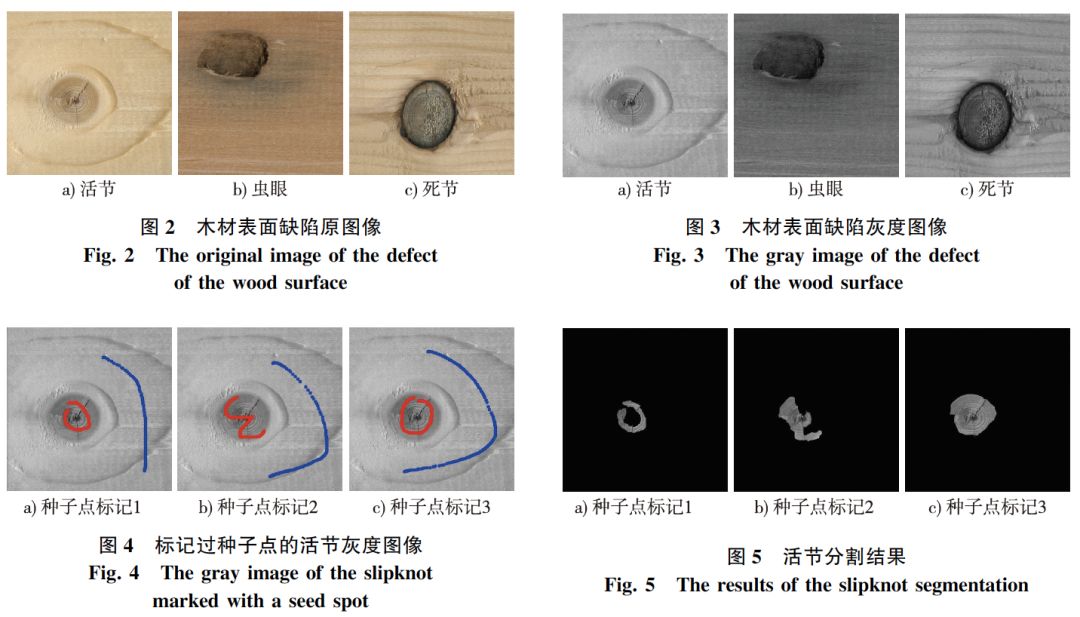
Graph Cuts 算法是基于像素級(jí)的分割,不能準(zhǔn)確評(píng)估像素屬于前景或者背景的概率,由于活節(jié)缺陷邊緣與背景的灰度值差距較小,即使標(biāo)定的目標(biāo)種子點(diǎn)像素?cái)?shù)量很多(如圖4c),但仍存在較嚴(yán)重的欠分割情況。對(duì)應(yīng)圖4a、b、c的分割初始化時(shí)間分別為41140.06,41022.37和40904.52ms,圖像分割所用時(shí)間分別為146268.57,278338.17和388243.09ms。可見(jiàn),種子點(diǎn)素?cái)?shù)越多,初始化所用的時(shí)間越短,圖像分割所用的時(shí)間越長(zhǎng)。
2.1.2蟲(chóng)眼缺陷的圖像分割
采用同樣的方法對(duì)圖3b的蟲(chóng)眼缺陷圖像進(jìn)行分割:設(shè)置λ=1,3次人工標(biāo)記種子點(diǎn)的結(jié)果如圖6,對(duì)應(yīng)的分割結(jié)果如圖7。由試驗(yàn)結(jié)果可知,蟲(chóng)眼缺陷圖像的分割結(jié)果與活節(jié)缺陷分割相似,分割結(jié)果受標(biāo)定的前景/背景種子點(diǎn)像素?cái)?shù)量影響,且都存在一定的欠分割問(wèn)題。對(duì)應(yīng)圖7a、b、c的分割初始化時(shí)間分別為41152.20,41038.55和40894.37ms,圖像分割時(shí)間分別為177052.53,368657.00和417434.91ms。種子點(diǎn)素?cái)?shù)越多,初始化所用的時(shí)間越短,圖像分割所用的時(shí)間越長(zhǎng)。

2.1.3死節(jié)缺陷的圖像分割
對(duì)圖3c死節(jié)缺陷圖像進(jìn)行分割:設(shè)λ=1,3次人工標(biāo)記種子點(diǎn)的結(jié)果如圖8,對(duì)應(yīng)的分割結(jié)果如圖9。可見(jiàn),采用Graph Cuts算法對(duì)標(biāo)注像素點(diǎn)多的死節(jié)缺陷圖像能夠?qū)崿F(xiàn)完整分割,但死節(jié)缺陷的分割輪廓曲線(xiàn)不平滑,且存在部分過(guò)分割情況。對(duì)應(yīng)圖8a、b、c的初始化時(shí)間分別為40933.91,40921.05和40916.92ms,圖像分割所用時(shí)間分別為34677.35,371604.00和413967.44ms。
綜上所述,采用Graph Cuts算法對(duì)木材表面缺陷圖像進(jìn)行分割時(shí),由于Graph Cuts算法對(duì)能量函數(shù)采用一次性最小化,對(duì)目標(biāo)和背景的人工標(biāo)記的種子點(diǎn)選取十分重要,選取結(jié)果直接影響分割結(jié)果;且該算法對(duì)相鄰像素間的區(qū)分度較差,對(duì)活節(jié)和蟲(chóng)眼缺陷進(jìn)行分割時(shí)存在欠分割問(wèn)題,對(duì)死節(jié)缺陷進(jìn)行分割時(shí)出現(xiàn)過(guò)分割情況。該算法的初始化時(shí)間隨種子點(diǎn)標(biāo)記的像素?cái)?shù)的增加而縮短,運(yùn)行時(shí)間相反。
2.2基于Grab Cut算法的木材表面缺陷圖像分割
采用Grab Cut算法對(duì)含有單缺陷目標(biāo)、多缺陷目標(biāo)的木材表面缺陷圖像進(jìn)行分割試驗(yàn)。試驗(yàn)的參數(shù)設(shè)定為距離參數(shù)β=0.1和GMM更新迭代次數(shù)k=5。木材缺陷圖像為512×512的彩色圖像。在試驗(yàn)過(guò)程中,首先輸入相同的初始化矩形框。
2.2.1單缺陷目標(biāo)的圖像分割
1)單活節(jié)圖像分割:圖10a為單個(gè)活節(jié)樣本的原圖像,圖10b為初始化矩形框,圖10d為分割結(jié)果,圖10c為分割結(jié)果的局部放大圖,圖10e為分割結(jié)果與原圖像的掩模。雖然活節(jié)缺陷的像素灰度值與背景的灰度值的差距較小,但Grab Cut算法仍然可以得到完整的分割輪廓, 分割時(shí)間為108144.784ms。由圖10e可見(jiàn),分割結(jié)果與原圖的吻合度較高,分割效果較好;從圖10c分割結(jié)果局部放大圖可見(jiàn),Grab Cut算法進(jìn)行圖像分割時(shí),會(huì)使活節(jié)缺陷內(nèi)部出現(xiàn)零星的欠分割區(qū)域。
2)單蟲(chóng)眼圖像分割:圖11a為單蟲(chóng)眼樣本的原圖像,圖11b為初始化矩形框,圖11d為分割結(jié)果,圖11c為分割結(jié)果的局部放大圖,圖11e為分割結(jié)果與原圖像的掩模。雖然活節(jié)缺陷的像素灰度值與背景的灰度值的差距較小,但Grab Cut算法仍然可以得到完整的分割輪廓, 分割時(shí)間為87329.92ms。由圖11e可見(jiàn),分割結(jié)果與原圖的吻合度較高,分割效果較好;從圖11c分割結(jié)果局部放大圖可見(jiàn),Grab Cut算法進(jìn)行圖像分割時(shí),會(huì)使蟲(chóng)眼缺陷內(nèi)部出現(xiàn)零星的欠分割區(qū)域。

3)單死節(jié)圖像分割:圖12a為單蟲(chóng)眼樣本的原圖像,圖12b為初始化矩形框,圖12d為分割結(jié)果,圖12c為分割結(jié)果的局部放大圖,圖12e為分割結(jié)果與原圖像的掩模。雖然活節(jié)缺陷的像素灰度值與背景的灰度值的差距較小,但Grab Cut算法仍然可以得到完整的分割輪廓, 分割時(shí)間為77545.63ms。由圖12e可見(jiàn),分割結(jié)果與原圖的吻合度較高,分割效果較好;從圖12c分割結(jié)果局部放大圖可見(jiàn),Grab Cut算法進(jìn)行圖像分割時(shí),會(huì)使蟲(chóng)眼缺陷內(nèi)部出現(xiàn)零星的欠分割區(qū)域。

綜上所述,Grab Cut算法進(jìn)行木材表面缺陷分割,能夠得到完整的分割輪廓,且不受背景噪聲影響,分割速度快,且對(duì)目標(biāo)與背景像素差別較大的死節(jié)和蟲(chóng)眼缺陷分割速度更快,但分割結(jié)果均會(huì)出現(xiàn)少量的欠分割問(wèn)題。
2.2.2多缺陷目標(biāo)的圖像分割
1)多活節(jié)缺陷分割試驗(yàn)(圖13):圖13a為多活節(jié)樣本的原圖像,圖13b為初始化矩形框,圖13c為分割結(jié)果,圖13d為分割結(jié)果與原圖像的掩模。可見(jiàn),Grab Cut算法能將木材表面的每一個(gè)活節(jié)缺陷都分割出來(lái),且分割輪廓曲線(xiàn)完整,分割結(jié)果與原圖的吻合度較高,但在背景中識(shí)別出兩個(gè)過(guò)分割噪點(diǎn),分割時(shí)間為13.337s。
2)多蟲(chóng)眼缺陷分割試驗(yàn)(圖14):由圖14可見(jiàn),Grab Cut算法能將木材表面的每一個(gè)蟲(chóng)眼缺陷都分割出來(lái),且分割輪廓曲線(xiàn)完整,分割效果好,分割結(jié)果與原圖吻合度較高,分割時(shí)間為10.913s。
3)多死節(jié)缺陷分割試驗(yàn)(圖15):由圖15可見(jiàn),

Grab Cut算法能將木材表面的每一個(gè)死節(jié)缺陷都分割出來(lái),且分割輪廓曲線(xiàn)完整,但是右下角死節(jié)缺陷的輪廓上存在少量過(guò)分割噪點(diǎn),分割時(shí)間為11.634s。
由圖13、14、15的分割結(jié)果可知,Grab Cut算法能夠快速鎖定多個(gè)木材表面缺陷的邊界輪廓,且不受木材表面缺陷的多少、大小和缺陷輪廓形狀的影響,分割效果好,分割速度快,抗噪性強(qiáng),運(yùn)行時(shí)間短。但是Grab Cut算法對(duì)木材表面缺陷分割時(shí)會(huì)出現(xiàn)零星的欠分割或者過(guò)分割情況,且分割前需要用戶(hù)人工畫(huà)定初始化矩形框。
3、結(jié)論
本研究采用Graph Cuts算法及其改進(jìn)算法Grab Cuts對(duì)木材表面缺陷圖像進(jìn)行分割試驗(yàn),分別從木材的單節(jié)、蟲(chóng)眼、死節(jié)出發(fā),做缺陷的單項(xiàng)和多項(xiàng)Grab Cut分割試驗(yàn),對(duì)分割的試驗(yàn)數(shù)據(jù)進(jìn)行分析。試驗(yàn)表明:目標(biāo)和背景的種子點(diǎn)選取直接影響Graph Cuts算法的分割結(jié)果,Graph Cuts算法的計(jì)算效率較低,分割時(shí)間較長(zhǎng),對(duì)相鄰像素間的區(qū)分度較差,分割結(jié)果不理想。改進(jìn)后的Grab Cut算法是迭代的Graph Cuts,該方法雖然在圖像分割前也需要人工畫(huà)定初始化矩形框,但操作相對(duì)簡(jiǎn)單,分割結(jié)果能夠得到完整的閉合缺陷區(qū)域邊界,且不受木材表面缺陷的類(lèi)型、數(shù)量、尺寸和缺陷形狀的影響,分割效果好,分割速度快,抗噪性強(qiáng),對(duì)灰度圖像和彩色圖像都可使用。由此我們可以對(duì)木材進(jìn)行圖像檢測(cè),以減少選取存在缺陷的木材,降低成本,提高木材的利用率。
審核編輯:郭婷
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4372瀏覽量
64307 -
效率
+關(guān)注
關(guān)注
0文章
151瀏覽量
20405
原文標(biāo)題:基于圖割算法的木材表面缺陷圖像分割
文章出處:【微信號(hào):vision263com,微信公眾號(hào):新機(jī)器視覺(jué)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
基于GAC模型實(shí)現(xiàn)交互式圖像分割的改進(jìn)算法
機(jī)器視覺(jué)表面缺陷檢測(cè)技術(shù)
機(jī)器視覺(jué)有助于解決表面缺陷
PCB缺陷檢測(cè)中圖像分割算法

一種改進(jìn)的圖像分割算法分析
基于粒子群FODPSO算法的圖像分割
基于圖割理論的尺度自適應(yīng)人臉跟蹤算法
一種新的彩色圖像分割算法
SAR圖像海陸分割算法






 基于圖割算法的木材表面缺陷圖像分割
基于圖割算法的木材表面缺陷圖像分割










評(píng)論