系統和設計工程師通常使用噪聲系數來確保最佳信號性能。然而,在信號鏈中使用混頻器會給簡單的噪聲系數分析帶來挑戰。本教程首先檢查噪聲系數的基本定義,然后對涉及混頻器的級聯模塊進行基于方程的分析,然后是測量噪聲系數的典型實驗室技術。本教程還介紹了噪聲溫度和Y因子噪聲測量的概念,然后探討了使用Y因子方法進行混頻器噪聲系數測量。討論了雙邊帶(DSB)和單邊帶(SSB)噪聲系數測量的示例。
介紹
噪聲系數的一般概念已被系統和電路設計人員很好地理解和廣泛使用。特別是,它用于傳達產品定義人員和電路設計人員的噪聲性能要求,并預測接收器系統的整體靈敏度。
當混頻器是信號鏈的一部分時,噪聲系數分析的主要困難就出現了。所有實際混頻器都圍繞本振(LO)頻率折疊RF頻譜,從而創建一個輸出,其中包含根據f外= |f射頻, G瞧|.在外差架構中,其中一個貢獻通常被認為是虛假的,另一個是有意的。因此,可能會采用圖像拒絕過濾或圖像消除方案來在很大程度上消除這些響應之一。在直接變頻接收器中,情況有所不同;兩個邊帶(高于和低于 F射頻= f瞧) 被轉換并用于所需信號。因此,這確實是混頻器的雙邊帶(DSB)應用。
工業中常用的各種定義在不同程度上解釋了噪聲折疊。例如,傳統的單邊帶噪聲因數F單邊 帶,假設允許來自兩個邊帶的噪聲折疊到輸出信號中。但是,只有一個邊帶可用于傳達所需信號。這自然會導致噪聲系數增加3dB,假設兩個響應的轉換增益相等。相反,DSB噪聲系數假設混頻器的兩個響應都包含所需信號的一部分,因此噪聲折疊(以及相應的信號折疊)不會影響噪聲系數。DSB噪聲系數適用于直接變頻接收器以及射電天文接收器。然而,更深入的分析表明,設計人員僅僅為給定應用選擇正確的噪聲系數“風味”,然后在標準弗里斯方程中替換相應的數字是不夠的。這樣做可能會導致嚴重的錯誤分析,當混頻器或混頻器后面的組件在確定系統噪聲系數方面起著不可忽視的作用時,這種情況可能特別嚴重。
本教程將噪聲系數的基本定義、涉及混頻器的級聯模塊的基于方程的分析以及測量噪聲系數的典型實驗室技術結合在一起。在其中,我們展示了級聯噪聲系數方程如何通過一個或多個混頻器的存在進行修改,并推導出許多流行的下變頻架構的適用方程。然后,我們描述了噪聲系數測量的Y因子方法,使用混頻器作為被測器件(DUT)。使用混頻器作為DUT可以確定適當的混頻器噪聲系數測量方法,這些方法可以有效地應用于級聯方程。
混頻器噪聲的概念模型
可視化混頻器噪聲貢獻的一種方法是考慮混頻器的概念模型(圖 1)。該模型基于安捷倫 Genesys 仿真程序提供的模型。1
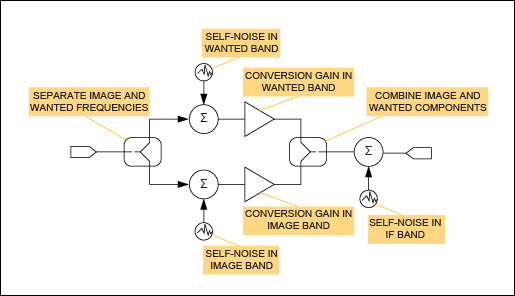
圖1.混頻器噪聲貢獻。
在該模型中,輸入信號被分成兩個獨立的信號路徑,一個表示高于LO的RF頻率,另一個表示低于LO的頻率。每條路徑都受到混頻器中獨立的加性噪聲處理,并施加獨立的轉換增益。最后,將兩條路徑轉換為IF頻率,并與混頻器輸出級中可能產生的進一步噪聲貢獻相加。每單位帶寬的自噪聲功率在所需波段和鏡像波段中可能不同;相應的轉換增益也可能不同。
為方便起見,我們可以將所有噪聲源引用到輸出,并將它們收集到全局噪聲項 N一個,表示混頻器輸出端口每單位帶寬的總額外噪聲功率。
N一個= NSGS+ N我G我+ N如果
請注意,N一個完全不依賴于混頻器輸入端口是否存在信號。
總結了混頻器的內部噪聲源后,我們現在轉向源端接引起的噪聲(圖2)。我們確定了兩個離散噪聲源,分別代表由于源端接在所需頻率和鏡像頻率下的輸入噪聲密度。我們必須將這些視為獨立的量,因為應用電路可能導致其中一個衰減,而另一個以低損耗傳輸到混頻器的RF輸入端口。如果圖像和所需的RF頻率很好地分離并且采用頻率選擇性匹配,則可能會出現這種情況。
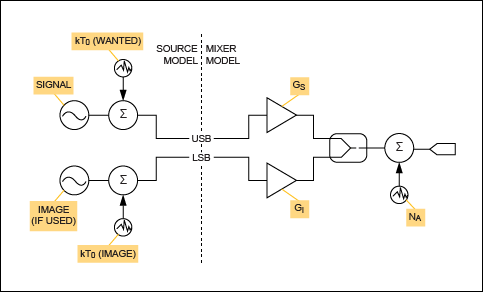
圖2.源噪聲和混頻器噪聲貢獻。
在寬帶匹配的情況下,我們可以寫 N外= N一個+ 千噸0GS+ 千噸0G我.但是,在所需RF頻率下與混頻器進行高Q值頻率選擇性匹配的情況下,由于源端接在鏡像頻率處,輸出端的噪聲可能可以忽略不計,導致N外= N一個+ 千噸0GS.通常,我們可以為混頻器輸入端口在鏡像頻率下可用的輸入源端終端噪聲功率的有效比例分配一個系數α。因此,N外= N一個+ 千噸0GS + αkT0G我,其中 α 是 0 ≤ α ≤ 1 范圍內的特定于應用的系數。稍后我們將看到應用中的有效噪聲系數取決于α的值。
噪聲系數定義
在討論為什么級聯噪聲系數計算會產生誤導之前,我們應該回顧一下該術語的一些基本定義。
解釋雙端口網絡的噪聲因數 (F) 的合理起點是:
F = (SNRIN)/(SNROUT)
當以dB表示時,稱為噪聲系數(NF):
NF = 10log10(F)
此表達式取決于輸入信號的信噪比。然而,如果未定義SNR,則該度量作為電路或組件本身的性能度量毫無意義,因為它在很大程度上取決于饋送信號的質量。因此,最好假設輸入端的SNR處于最佳情況,即唯一的噪聲源是由于輸入端接在某個定義溫度下的熱噪聲引起的。假設噪聲因數不依賴于所使用的信號電平也是合乎邏輯的。這假定所表征的雙端口網絡位于其線性工作區域中。如果我們讓輸入信號功率為 P 可以看出這一點在信號增益為Gs.然后,輸出功率由P外= GsP在和:
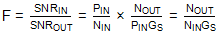
此外,這些噪聲功率,N在和 N外,定義不明確,除非我們指定測量它們的帶寬。這可以通過指定 N 來解決在和 N外表示任何給定指定輸入和輸出頻率下每單位帶寬的噪聲功率。
單邊帶噪聲因數
上述考慮因素有助于解釋IEEE噪聲因子定義的基本原理:
噪聲系數(噪聲系數)(雙端口傳感器)。在指定的輸入頻率下)輸出端口可用相應輸出頻率下每單位帶寬的總噪聲功率與2)在標準噪聲溫度(1K)下由輸入端接在輸入頻率處產生的那部分290)之比。
注1:對于外差系統,原則上將有多個輸出頻率對應于單個輸入頻率,反之亦然;對于每對相應的頻率,定義一個噪聲因子。
注2:短語“在輸出端口可用”可以替換為“由系統傳送到輸出端接”。
注3:僅當指定了輸入端接時,通過噪聲因子來表征系統才有意義。
噪聲因數的這個定義是輸出頻率的點函數,相對于一個相應的RF頻率,而不是同時對RF頻率,這就是使其成為單邊帶(SSB)噪聲因數的原因(見圖3)。
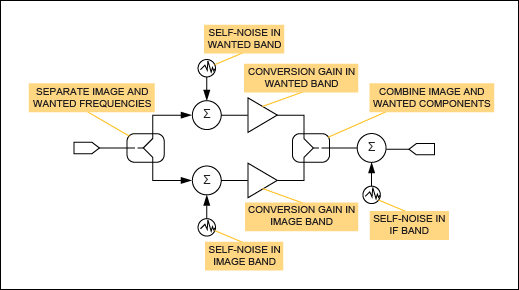
圖3.SSB 噪聲系數。
需要注意的是,分母僅包括來自一個邊帶的噪聲;分子包括相應輸出頻率下每單位帶寬的總噪聲功率,而不進行任何特定排除。為了在具有信號和圖像響應的混頻器的情況下以數學形式明確這一點,上述定義可以寫成:
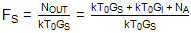
其中 G我是鏡像頻率下的轉換增益;GS是信號頻率處的轉換增益;T0是標準噪聲溫度;和 N一個是在輸出端子測量的混頻器電子元件增加的每單位帶寬的噪聲功率。鏡像頻率對應的噪聲因子可以寫成:
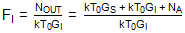
如果鏡像頻率處的轉換增益與所需信號頻率處的轉換增益不同,則此數字不同。有些人將上述IEEE定義解釋為將圖像噪聲從術語“輸出端口可用的相應輸出頻率下每單位帶寬的總噪聲功率”中排除。3因此,他們假設:
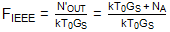
該定義對應于鏡像頻率處的源輸入噪聲完全從混頻器的輸入端口中排除的情況。這種解釋并未被行業從業者廣泛使用。不過,為了完整起見,如圖 4 所示。
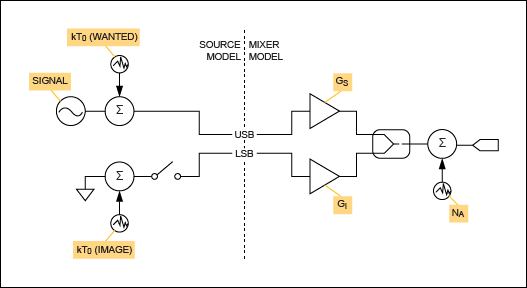
圖4.SSB噪聲系數的IEEE變體。
美國聯邦標準 1037C 對噪聲因數有以下定義:
噪聲系數:在標準噪聲溫度(通常為290K)下,器件的輸出噪聲功率與輸入端接中可歸因于熱噪聲的部分之比。注意:因此,噪聲系數是實際輸出噪聲與設備本身不引入噪聲時剩余噪聲的比率。在外差系統中,輸出噪聲功率包括鏡像頻率變換的雜散貢獻,但在標準噪聲溫度下,輸入端接中可歸因于熱噪聲的部分僅包括通過系統主頻率變換出現在輸出中的部分,不包括通過鏡像頻率變換出現的部分。同義詞噪聲因子。
由于這個較新的定義明確包括輸出噪聲功率中鏡像頻率變換的雜散貢獻,因此SSB噪聲因數可以按照前面的建議編寫:
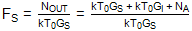
讓我們考慮 G 的情況S= G我.然后:
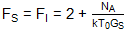
如果我們進一步考慮混音器本身不增加噪聲的情況,N一個= 0,那么我們剩下 F = 2 或 NF = 3.01dB。這與無噪聲混頻器的SSB噪聲系數為3dB的說法相對應。
雙邊帶噪聲因數
在某些情況下,“系統原理變頻”不是適用的術語;這兩種反應同樣需要和有用。示例包括輻射計和直接變頻接收器。在直接變頻接收器中,LO頻率位于所需信號的RF通帶的中心;混頻器的兩個響應構成整個所需信號頻譜的連續一半。圖 5 說明了這種情況。

圖5.DSB 噪聲系數。
因此,在這種情況下,考慮DSB噪聲因子是有意義的:
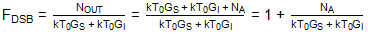
如果我們假設 Gs= G我然后:
FDSB= 1 + (N一個/(2kT0GS))
在相同的約束下:
FSSB = 2 + NA/(kT0GS)
因此,在兩個轉換增益相等的情況下,混頻器的SSB噪聲系數比相應的DSB噪聲系數高3dB。此外,如果混頻器不增加任何額外的噪聲(N一個= 0),則 FDSB= 1 或 NFDSB= 0分貝。
噪聲系數在級聯噪聲系數計算中的應用
基線案例:線性電路塊級聯
考慮以下三個放大器模塊的簡單級聯(圖 6)。
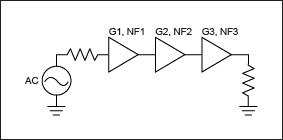
圖6.三個增益模塊級聯。
輸出端的總噪聲可計算如下:
NOUT = kT0G1G2G3 + NA1 G2G3 + NA2G3 + NA3
由級聯輸入端的熱噪聲引起的輸出端噪聲為:
NOT = kT0G1G2G3
這意味著整體噪聲因子為:
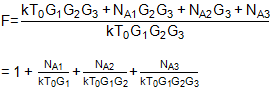
代:
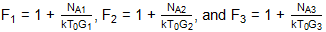
收益 率:
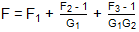
這可以被認為是三個塊的標準弗里斯級聯噪聲方程。從這里擴展到任意數量的塊是微不足道的。
外差轉換級
考慮接收器信號路徑中的以下頻率轉換級(圖 7)。混頻器的DSB噪聲系數為3dB,轉換增益為10dB。所需載波頻率為2000MHz,LO選擇為1998MHz,因此所需頻率和鏡像頻率都在濾波器的通帶內。
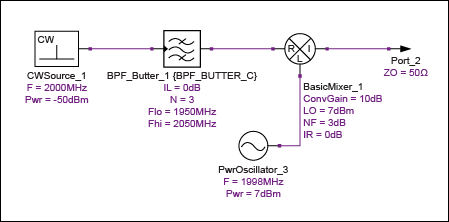
圖7.無鏡像抑制的外差級。
表1總結了這種布置的級聯性能,其中CF是信道頻率,CNP是信道噪聲功率(以1MHz帶寬測量),增益是級增益,CG是級聯增益,包括當前級,CNF是級聯噪聲系數。
| 部件 | CF (兆赫) | 壓縮液 (分貝) | 增益(分貝) | CG (分貝) | 碳氫氟 (分貝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 2 | -97.965 | 10 | 9.999 | 6.011 |
| *濾鏡無圖像抑制。 | |||||
這兩個模塊的總級聯增益為9.999dB,而SSB噪聲系數為6.011dB。從前面的分析中可以正確預測到該噪聲系數,因為我們預計SSB噪聲系數比混頻器的DSB系數高3.01dB。由于濾波器的有限插入損耗,噪聲系數還會下降。總體而言,這一結果符合我們的預期。
現在我們考慮相同的情況,但LO頻率恢復到1750MHz(圖8)。在此LO頻率值下,鏡像為1500MHz,遠遠超出混頻器前面濾波器的通帶。
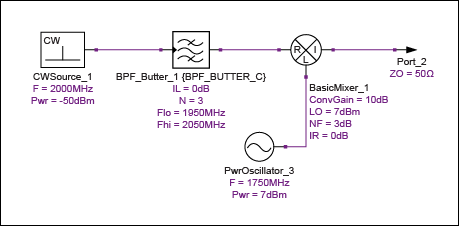
圖8.具有鏡像抑制功能的外差級。
表2總結了這種安排的級聯性能。所需信號的增益與以前相同,但級聯噪聲系數(CNF)已更改為4.758dB的值。
| 部件 | CF (兆赫) | 壓縮液 (分貝) | 增益(分貝) | CG (分貝) | 碳氫氟 (分貝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 250 | -99.218 | 10 | 9.999 | 4.758 |
| *濾鏡的顯著圖像抑制。 | |||||
為了解釋這一結果,我們需要考慮這種情況下的噪聲情況與圖4所示的情況相似。具體而言,源阻抗鏡像噪聲被抑制。混頻器級增加的噪聲可以通過先前推導的DSB噪聲因子公式計算得出:
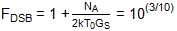
因此:
NA = 2kT0GS(10(3/10) - 1)
現在混頻器輸出端的總噪聲由N給出外= N一個+ 千噸0GS + αkT0G我,在此應用程序中為 α = 0。因此:
NOUT = 2kT0GS(10(3/10) - 1) + kT0GS
得到的噪聲系數可以寫成:
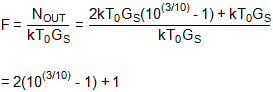
以dB表示,我們有:
NF = 10log10(2(10(3/10)- 1) + 1) = 4.757dB
這應該與4.758dB的仿真值進行比較,其中包括濾波器插入損耗的微小額外貢獻。
通常,混頻器級的有效SSB噪聲系數由下式給出:
FSSBe= 2(FDSB– 1) + 1 + α
其中a = 0表示鏡像頻率處的端接噪聲得到良好抑制的情況,α = 1表示完全沒有抑制的情況。請注意,如果α = 1,則有效單邊帶(SSB)噪聲系數降至FSSBe= 2樓DSB,這是本節開頭說明的情況。在某些情況下,可能會出現分數值,例如,如果鏡像抑制濾波器不直接耦合到混頻器輸入端子,或者圖像和所需響應之間的頻率間隔不大。
外差接收器
通過圖9中的示例,我們可以看到如何在更大的級聯分析中應用有效噪聲系數。為了計算整個鏈的級聯噪聲系數,我們需要將混頻器及其相關的LO和鏡像抑制濾波封裝為具有特定增益和噪聲系數的等效雙端口網絡。該雙端口網絡的有效噪聲因數為 FSSBe= 2(FDSB– 1) + 1,因為鏡像頻率處的端接噪聲被前置濾波器很好地抑制了。
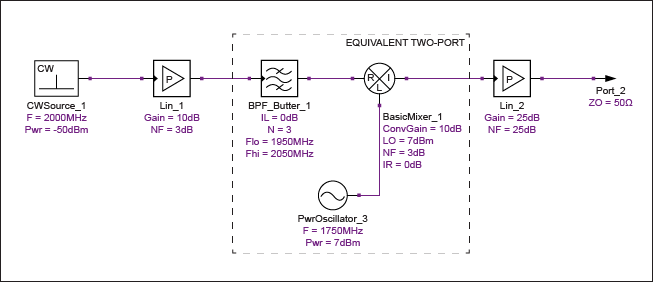
圖9.相鄰系統模塊環境中的外差混頻器。
請注意,適用的噪聲系數既不是混頻器的DSB,也不是SSB噪聲系數。相反,它是一個介于這兩個值之間的有效噪聲數字。在這種情況下,DSB噪聲系數為3dB,雙端口網絡的等效噪聲系數可以計算為4.757dB,如上所述。在整個級聯計算中使用該值得出的系統噪聲系數為7.281dB,如表3所示。手動計算表明,該結果與使用4.757dB作為混頻器噪聲系數的標準弗里斯方程一致。
| 部件 | CF (兆赫) | 壓縮液 (分貝) | 增益(分貝) | 信噪比 (分貝) | CG (分貝) | 碳氫氟 (分貝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 | 0 |
| Lin_1 | 2000 | -100.975 | 10 | 3 | 10 | 3 |
| BPF_Butter_1 | 2000 | -100.976 | -7.12E-04 | 7.12E-04 | 9.999 | 3 |
| BasicMixer_1 | 250 | -90.563 | 10 | 3 | 19.999 | 3.413 |
| Lin_2 | 250 | -61.695 | 25 | 25 | 44.999 | 7.281 |
通常,當用等效的雙端口網絡代替混頻器及其相鄰組件時,輸入端口應該是信號流中鏡像響應被拒絕的最新節點。輸出端口應該是圖像和所需響應組合在一起的最早節點(通常是混音器的輸出端口)。如果混頻器的圖像響應沒有被架構有效抑制,那么弗里斯方程就不能不修改地使用。
零中頻接收器
現在考慮零中頻(ZIF)或直接變頻接收器(圖10)。
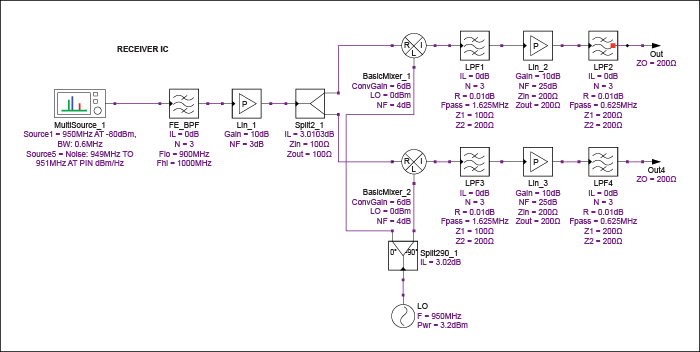
圖 10.帶有低噪聲放大器 (LNA)、混頻器、濾波器和可變增益放大器 (VGA) 的 ZIF 接收器。
該系列包括一個具有10dB增益和3dB噪聲系數的LNA;以950MHz為中心的帶通濾波器;信號分配器,用于將信號發送到一對混頻器,每個混頻器的轉換增益為6dB;DSB噪聲系數為4dB。VGA的定義增益為10dB,噪聲系數為25dB。對該陣容的仿真產生了表4所示的結果,其中CP是通道功率,SNF是級噪聲系數。其他項目與前面的表相同。
| 部件 | CF (兆赫) | CP (分貝) | 壓縮液 (分貝) | 增益(分貝) | 信噪比 (分貝) | CG (分貝) | 碳氫氟 (分貝) |
| MultiSource_1 | 950 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 |
-1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
在表5中,我們顯示了使用傳統弗里斯公式計算級聯噪聲系數的結果。與顯示模擬器結果的表 4 的主要區別在于最后一列 CNF。
| 部件 |
F (分貝) |
增益(分貝) | CG (分貝) | 碳氫氟 (分貝) |
| 低頻濾波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 攪拌機 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 12.65 |
| LPF2 | 0.01 | -0.01 | 22.93 | 12.65 |
顯然,級聯噪音數字出了問題。我們使用電子表格估計12.64dB,但模擬器發現10.16dB。級聯增益匹配得相當好,但我們需要確定哪個噪聲數據是有效的。首先,我們對整個結構的DSB噪聲系數感興趣,因為整個ZIF結構在兩個邊帶中使用信號,并且在兩個邊帶中都受到噪聲的影響。因此,有必要得出涉及放大器的級聯的DSB噪聲系數,然后是混頻器,然后是附加放大器(圖11)。
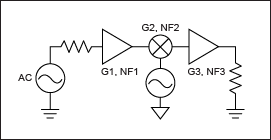
圖 11.級聯,包括混音器。
輸出端的總噪聲密度可計算為:
NOUT = 2kT0G1G2G3 + 2NA1G2G3 + NA2G3 + NA3
由級聯輸入端的熱噪聲引起的輸出端噪聲為:
NOT = 2kT0G1G2G3
這意味著整體噪聲因子為:
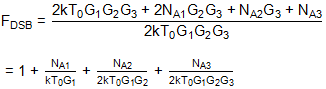
代:
F1 = 1 + NA1/(kT0G1), F2DSB = 1 + NA2/(2kT0G2), and F3 = 1 + NA3/(kT0G3)
收益 率:
FDSB = F1 + (F2DSB - 1)/G1 + (F3 - 1)/(2G1G2)
該推導表明,有必要在級聯方程中使用混頻器的DSB噪聲系數,并且對于級聯噪聲系數,所有后續階段的噪聲貢獻必須除以2,相對于弗里斯方程的通常形式。未能執行后一除以 2 會導致表 5 中所示的電子表格方程分析出錯。在混頻器之后修改電子表格單元格中的方程式以包括必要的除以2,得到的結果如表6所示。
| 部件 | F (分貝 | 增益(分貝) | CG (分貝) | 碳氫氟 (分貝) |
| 低頻濾波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| 液化天然氣 | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 攪拌機 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 10.17 |
| LPF2 | 0.01 | -0.01 | 22.93 | 10.17 |
表4和表6之間的一致性現在很好。然而,這個練習也證明了直接代入涉及混頻器的弗里斯級聯方程的危險。
接下來,我們考慮相同的情況,但所需信號比LO高300kHz。框圖如圖10所示,但所有信號都落在LO的高端。這使其成為相同接收器架構的低中頻(LIF)應用。使用與以前相同的 Genesys 仿真工作區,結果如下表 7 所示。
| 部件 | CF (兆赫) | CP (分貝) | 壓縮液 (分貝) | 增益(分貝) | 信噪比 (分貝) | CG (分貝) | 碳氫氟 (分貝) |
| MultiSource_1 | 950.3 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 |
-1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
這些結果與之前對相同架構的仿真相似,只是噪聲系數增加了3dB。事實上,即使該系統的所有組件都是無噪聲的,除了源電阻外,噪聲系數也將為3dB。從本質上講,這是復雜接收器結構的SSB應用,并且沒有抑制不需要的邊帶的措施。級聯噪聲系數的推導與已經給出的相同,只是級聯輸入端熱噪聲引起的輸出噪聲再次為:
NOT = kT0G1G2G3
所以現在:
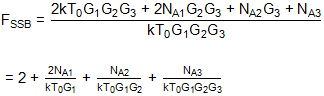
代:
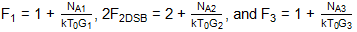
收益 率:
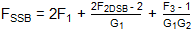
正如預期的那樣,噪聲級聯方程中的每個項都乘以2,相對于這種結構的DSB用例。但是,這種情況有些人為。我們現在有一個接收器,在噪聲和干擾方面對兩個邊帶都敞開,但它僅用于其中一個邊帶中的信號。由于較低的邊帶只會增加接收器的脆弱性,因此使用正交通道為不需要的邊帶提供抑制是有意義的。一種解決方案是將接收器輸出端的I和Q信號與90度合路器相結合,從而消除不需要的邊帶中的信號,同時建設性地將它們添加到所需的邊帶中。這實際上會將整個接收器轉換為鏡像抑制下變頻器。最終組合級將系統噪聲系數恢復先前損失的3dB,假設被組合信號的相位在組合點得到足夠好的控制。這種方案的仿真原理圖如圖12所示,相應的結果如表8所示。
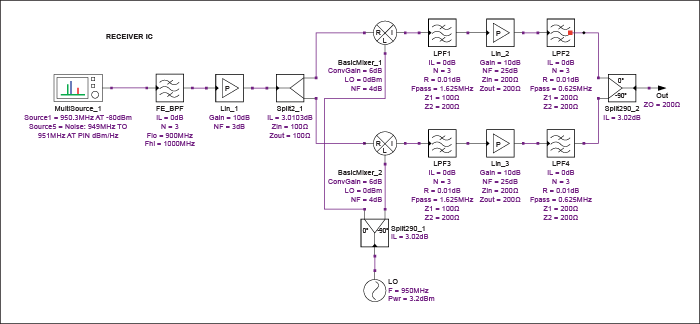
圖 12.靠近具有鏡像抑制功能的ZIF接收器。
| 部件 | CF (兆赫) | CP (分貝) | 壓縮液 (分貝) | 增益(分貝) | 信噪比 (分貝) | CG (分貝) | 碳氫氟 (分貝) |
| MultiSource_1 | 950.3 | -79.995 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.005 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950.3 | -70.004 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950.3 | -73.014 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0.3 | -67.053 | -96.441 | 5.958 | 4 | 12.938 | 6.815 |
| LPF1 | 0.3 | -67.005 | -96.443 | -1.64E-03 | 1.00E-02 | 12.936 | 6.815 |
| Lin_2 | 0.3 | -57.047 | -80.09 | 9.991 | 25 | 22.927 | 13.177 |
| LPF2 | 0.3 | -57.051 | -80.094 |
-3.82E-03 |
1.00E-02 | 22.923 | 13.177 |
| Split290_2 | 0.3 | -54.062 | -80.145 | 3.001 | 3.02 | 25.923 | 10.125 |
在最后(組合)階段,級聯噪聲系數(CNF)提高了3dB,表明噪聲系數如預期的那樣恢復了。
事實證明,使用安捷倫 Genesys 模擬這些架構和場景與所研究案例中適當級聯噪聲系數的數學推導一致。?
對于討論和仿真的每個架構,表9總結了級聯噪聲因數方程。
| 結構 | 應用 | 級聯 F 方程 |
| 三個增益模塊 | 任何 |
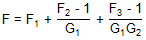 |
| 外差混頻器 | SSB,理想的圖像濾波 |

| 復雜下變頻器 | 齊夫 |
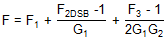 |
| 復雜下變頻器 | LIF,無圖像抑制 |
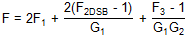 |
| 復雜下變頻器 | LIF,圖像拒絕組合 |
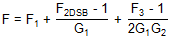 |
噪音溫度
為了討論Y因子噪聲測量,有必要介紹噪聲溫度的概念。在之前的方程中,我們使用了眾所周知的結果,即在給定溫度下,電阻器可獲得的噪聲功率譜密度為kT,W/Hz,其中k是玻爾茲曼常數,T是絕對溫度。如果我們假裝器件無噪聲,并且如果額外的噪聲功率頻譜密度由輸入端接的噪聲溫度等效升高高于參考溫度來解釋,則可以解釋設備中的所有噪聲源。噪聲因子可能與等效溫度T有關e,通過 F = 1 + Te/T0,其中 T0定義為290K的參考噪聲溫度。不出所料,噪聲因數 1 由器件的等效噪聲溫度 0K 表示,而噪聲因數 2 由 T 表示e= 290K。
Y 因子
用于噪聲系數測量的Y因子方法5涉及使用校準的噪聲源,該噪聲源具有兩種不同的噪聲溫度,具體取決于設備是否存在直流電源。校準源具有特征性的超噪比(ENR),定義為:
ENRdB = 10log10 [(TSON - TSOFF)/T0]
其中 TS上是源在其ON狀態下的噪聲溫度,T是S關閉是處于 OFF 狀態的相應值。Y因子是兩個噪聲功率電平的比值,一個在噪聲源打開時測量,另一個在噪聲源關閉時測量。
Y = NON/NOFF
由于源的噪聲功率可以直接用其噪聲溫度表示,因此我們也可以這樣寫:
Y = TON/TOFF
噪聲因子測量和計算
為了評估DUT的噪聲因數,我們必須將噪聲功率測量設備連接到DUT的輸出。讓 DUT 具有噪聲溫度 T1且儀器的噪聲溫度T2.雖然不可能消除測量設備的噪聲溫度(T2) 從任何給定的讀數中,我們可以測量 T12,這是 DUT 后跟儀器的綜合噪聲溫度。我們可以使用計算來隔離 T1自 T 以來12= T1+ T2/G1.因此,策略是使用直接連接到測量儀器的校準噪聲源進行Y因子測量,這將允許T2待定。我們有:
Y2 = N2ON/N2OFF = (TSON + T2)/(TSOFF + T2)
可以重新排列為:
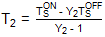
根據已知的T值獲得測量裝置的噪聲溫度S上和 TS關閉,下一步是測量 DUT 和測量儀器級聯的新 Y 因子:
Y12 = N12ON/N12OFF
這允許使用與以前相同的程序計算 DUT 和儀器的組合噪聲溫度:
T12 = (TSON - Y12 TSOFF)/(Y12 - 1)
之前存儲了兩個 N1上和 N1關閉現在可以訪問 N12上和 N12關閉,我們有足夠的信息來計算 DUT 的增益,如下所示:
G1= (N12ON - N12OFF)/(N2ON - N2OFF)
這提供了足夠的信息,可以使用以下方法在數學上減去測量儀器噪聲溫度的貢獻:
T1 = T12 - T2/G1
被測器之前的損失
如果在DUT之前存在已知損耗,則必須消除這些損耗的影響,以獲得DUT在其輸入T處的真實噪聲溫度1在.假設這些損失是吸收性的,可以使用以下等式:
T1IN = (T1/LIN) - ((LIN - 1)TL/LIN)
其中 TL是物理溫度的損耗和L在是要補償的插入損耗,表示為大于單位的線性功率比。
混頻器作為 DUT 在 Y 因子噪聲因子測定中
考慮到用于噪聲系數測量的校準噪聲源本質上是寬帶的,并且ON時噪聲溫度的任何微小變化都由嵌入在源中的詳細校準表處理。因此,任何未經修改的Y因子技術使用都會導致對混頻器的DSB噪聲系數的評估。這是因為校準后的噪聲源同時在兩個邊帶中注入噪聲功率,并且兩個邊帶的組合輸出噪聲功率有助于用于計算Y因子的輸出噪聲溫度。下面給出的兩個示例案例說明了如何在修改和不修改的情況下使用測量方法分別獲得DSB或SSB測量值。
通過Y因子法測量DSB噪聲系數的示例
為了說明所討論的概念,安捷倫 Genesys 仿真是通過向仿真的 DUT 中注入噪聲源來執行的,該 DUT 是一個混頻器,DSB 噪聲系數為 4.9dB,轉換增益為 8.8dB。注入的噪聲功率由變量PIN決定,PIN是一個掃描變量,迭代兩個可能的值-159dBm/Hz和-174dBm/Hz,分別代表噪聲源的ON和OFF條件。IF定義為250MHz,混頻器的RF端口的所需和鏡像響應分別為2000MHz和1500MHz(圖13)。仿真收集的唯一數據(表10和表11)是輸入(直接連接到噪聲源代替校準步驟)和輸出(代表測量模式)在100kHz帶寬內的通道噪聲功率。
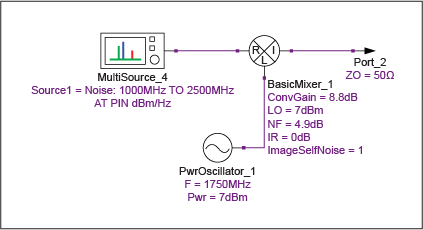
圖 13.使用Y因子方法確定DSB混頻器噪聲系數的仿真原理圖。
| B (赫茲) | IL (分貝)* | 引腳關閉 (分貝) | 引腳開啟 (分貝) | 噘嘴關閉 (分貝) | 噘嘴 (分貝) |
| 100,000 | 0 | -123.975 | -109 | -107.265 | -96.91 |
| *請注意,參數IL表示DUT之前的插入損耗,在本例中為0dB。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分貝) | 克 (分貝) |
| 31.443 | 10.851 | 606.147 | 0 | 606.147 | 606.147 | 4.9 | 8.8 |
請注意,T2表示儀器的噪聲溫度,這是可以接受的,因為在這種情況下,儀器是 Genesys 模擬器,它評估噪聲而不添加任何自己的噪聲。由于DUT之前的插入損耗為0dB,因此T1與 T 相同1在.Y因子測量的最終計算噪聲系數由F = 10log給出10(1 + 噸1在/290).獲得的值(4.9dB)與設置混頻器原理圖時使用的參數設置的預期值一致。
通過Y因子法測量SSB噪聲系數的示例
仿真原理圖如圖14所示,測試結果如表12和表13所示。
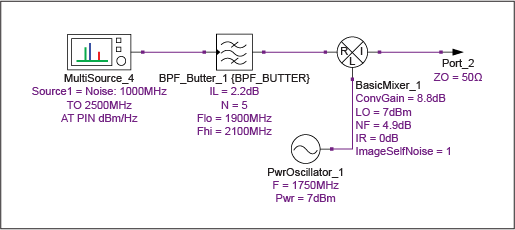
圖 14.使用Y因子方法確定SSB混頻器噪聲系數的仿真原理圖。
| B (赫茲) | IL (分貝)* | 引腳關閉 (分貝) | 引腳開啟 (分貝) | 噘嘴關閉 (分貝) | 噘嘴 (分貝) |
| 100,000 | 2.2 | -123.975 | -109 | -108.015 | -101.455 |
| *請注意,參數IL表示DUT之前的插入損耗,在本例中為2.2dB。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分貝) | 克 (分貝) |
| 31.443 | 4.529 | 2211.584 | 0 | 2211.584 | 1217.354 | 7.158 | 6.602 |
由于DUT之前的插入損耗為2.2dB,因此T1高于混頻器的噪聲溫度T1在,已根據 DUT 前損耗部分中的公式 42 計算得出。Y因子測量的最終計算噪聲系數由F = 10log給出10(1 + 噸1在/290).得到的值為7.158dB。該值應與公式43獲得的值進行比較,假設光源的鏡像噪聲被完全抑制:
NF = 10log10(2(10(4.9/10)- 1) + 1) = 7.144dB
由于濾波器具有有限的插入損耗,因此鏡像抑制濾波器在鏡像頻率下的阻抗并非完全無功。這反過來意味著源的像帶噪聲沒有完全抑制,這被認為是理想噪聲系數小幅增加的原因。
使用填充Y因子法測量SSB噪聲系數的示例
在這種方法中,我們應用衰減器來確保混頻器在所需頻率和鏡像頻率下都受到類似的“冷”(即關斷狀態)噪聲溫度的影響。這應該導致SSB噪聲系數更接近于比DSB噪聲系數高3dB的值,因為源端接的噪聲溫度不再受到濾波器的任何顯著影響(圖15,表14和15)。
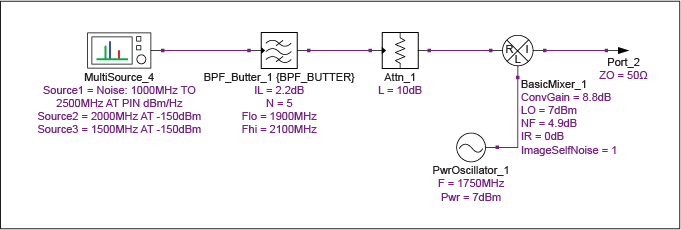
圖 15.使用填充Y因子方法確定SSB混頻器噪聲系數的仿真原理圖。
| B (赫茲) | IL (分貝)* | 引腳關閉 (分貝) | 引腳開啟 (分貝) | 噘嘴關閉 (分貝) | 噘嘴 (分貝) |
| 100,000 | 12.2 | -123.975 | -109 | -107.272 | -106.141 |
| *請注意,參數IL表示DUT之前的插入損耗,在本例中為12.2dB,表示濾波器和衰減器的總損耗。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分貝) | 克 (分貝) |
| 31.443 | 1.297 | 29392.313 | -5.98E-14 | 29392.313 | 1498.536 | 7.901 | -3.398 |
Y因子測量的最終計算噪聲系數由F = 10log給出10(1 + 噸1在/290).得到的值為7.901dB。該值與在3.0dB的DSB噪聲系數上增加4.9dB的預期值非常吻合。請注意,使用 10dB 衰減器會導致 Y 因子接近單位,這可能會危及精度。在實際測量中使用高衰減值時,建議選擇可用的最高ENR源以保持精度。
結論
在本教程中,我們看到,當混頻器是接收器級聯的一部分時,級聯噪聲因子的弗里斯方程通常使用DSB或SSB版本的混頻器噪聲系數都無效。在使用濾波器在很大程度上消除接收器的鏡像響應的情況下,可以用等效的雙端口網絡代替混頻器、濾波器和LO子系統。但是,產生的噪聲系數必須根據DSB噪聲系數計算,同時考慮耦合到混頻器輸入端口的源端接的頻率選擇性。
我們還發現,相同的物理結構可能具有不同的有效噪聲系數,這取決于信號是分布在LO周圍還是完全分布在LO的一側(即,應用分別是DSB或SSB)。在LIF模式下使用復數接收器引起的3dB信噪比損耗可以通過適當使用鏡像抑制組合、復數濾波或等效基帶處理來恢復。
Y因子測量評估混頻器的DSB噪聲系數,除非采取特殊措施來濾除鏡像頻率處的寬帶噪聲激勵。這是用于先前推導的級聯方程的適當值。當使用濾波器試圖獲得SSB噪聲系數時,有必要考慮所用濾波器的插入損耗。此外,濾波器的源端接鏡像噪聲抑制程度可能導致偏離SSB噪聲系數的經典定義。使用匹配衰減器可以在很大程度上克服這個問題,前提是使用的衰減量與噪聲源的ENR相比不會過大。
審核編輯:郭婷
-
接收器
+關注
關注
15文章
2563瀏覽量
73468 -
混頻器
+關注
關注
10文章
844瀏覽量
46718 -
無線電
+關注
關注
60文章
2163瀏覽量
117700
發布評論請先 登錄
ADC噪聲系數參數在數據轉換器中有哪些應用?
軟件無線電接收機的多速率處理技術研究
現代無線電接收機的系統噪聲系數分析一:級聯接收機的計算
現代無線電接收機的系統噪聲系數分析二:Y因子噪聲因子測量法
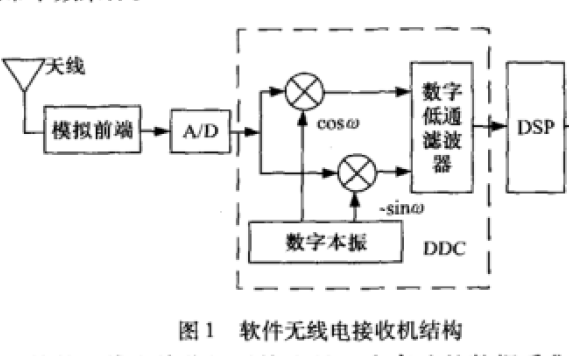
怎么樣使用PCI總線實現軟件無線電接收機系統的設計資料說明
基于專用DDC的軟件無線電接收機的設計






 現代無線電接收機的系統噪聲系數分析
現代無線電接收機的系統噪聲系數分析












評論