相量法是線性電路正弦穩態分析的一種簡易方法。
01 復 數
復數及其運算是應用相量法的基礎。
一個復數有多種表示形式。 復數F的代數形式為:
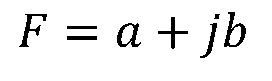
其中為虛單位。 a稱為復數F的實部,b成為復數F的虛部。 復數F在復平面上是一個坐標點,常用原點至該點的向量表示,如下圖所示。

圖1 復數的表現形式
根據上圖,可得到復數F的三角形式為:
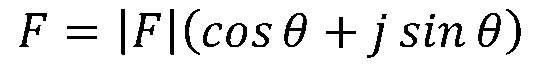
復數F的指數形式或極坐標形式為:

式中| F|為復數的模值,θ為復數的輻角,可以用弧度或度表示。 他們之間的關系為:
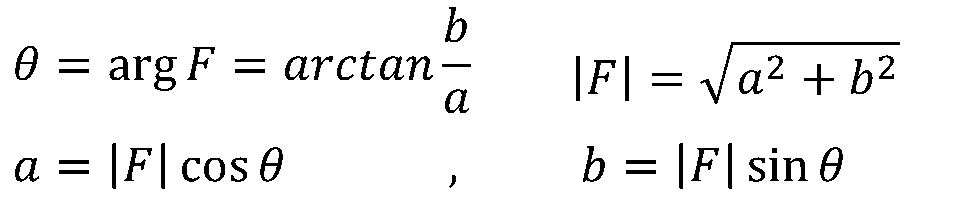
有時候還使用Re[F]=a表示取復數F的實部,Im[F]=b表示F的虛部;
F*表示復數F的共軛復數,即

注:兩個實部相等,虛部互為相反數的復數互為共軛復數。
1.1復數加減運算
復數的相加和相減。
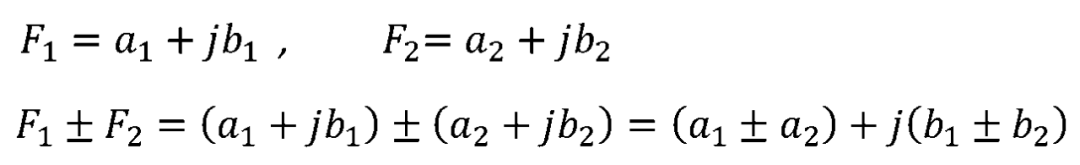
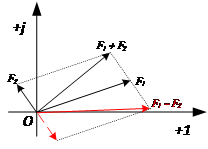
復數的加減運算可以使用平行四邊形法在復平面上用向量的相加和相減求得。
1.2復數的乘除運算
復數相乘使用指數形式較為方便
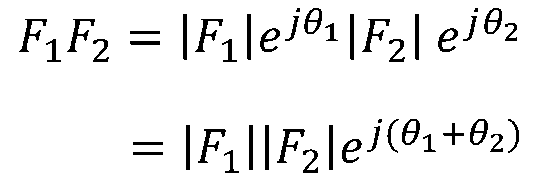
故
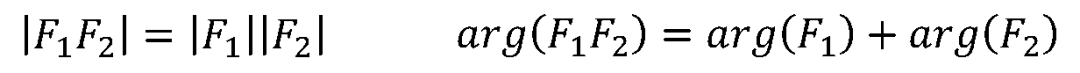
用代數形式表示為:
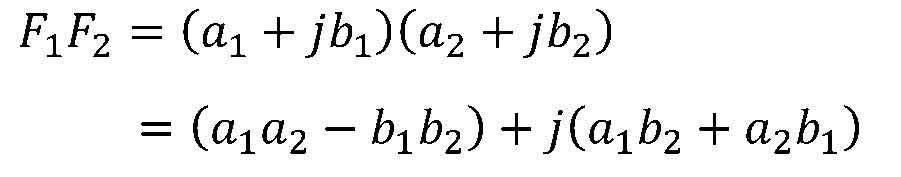
復數相除運算為:
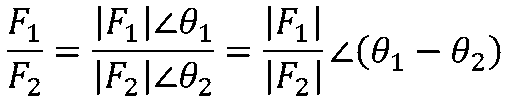
故有
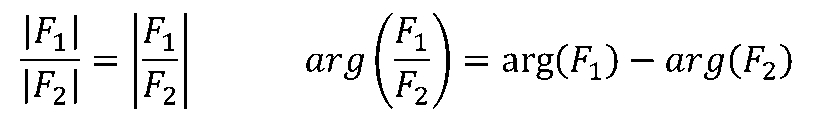
代數形式:
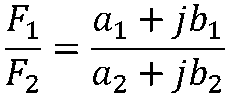
后續可以上下同乘以F2的共軛復數進行有理化運算。 復數乘以共軛復數為實數。
復數乘除運算圖解如下圖所示:

從上圖可以看出:復數乘、除表示為模的放大或縮小,輻角表示為逆時針旋轉或順時針旋轉。
復數
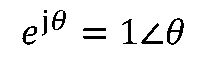
是一個模等于1,輻角為θ的復數。 任意復數
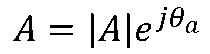
乘以于把復數A逆時針旋轉一個角度θ,而A的模不變,故稱為旋轉因子。
根據歐拉公式,
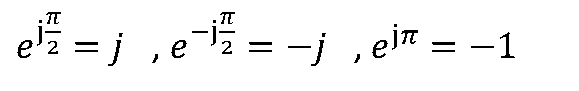
。 因此“±j“和”-1“都可以看成旋轉因子。
例如一個復數乘以j等于把該復數在復平面上逆時針旋轉π; 要給復數除以j等于把該復數乘以-j,因此等于把它順時針旋轉π/2。
02 正 弦 量
電路中按照正弦規律變化的電壓或電流,統稱為正弦量。
若在電路中有正弦電流i,指定參考方向下,其數學表達式如下:
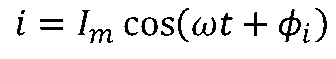
式中的3個常數
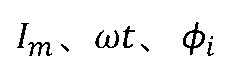
稱為正弦量的三要素。
Im稱為正弦量的振幅,它是正弦量在整個振蕩過程中達到的最大值,也是正弦量的極大值。
隨時間變化的角度稱為正弦量的相位,或相角。 ω稱為正弦量的角頻率,它是正弦量的相位隨時間變化的角頻率,即:
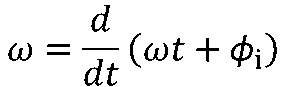
單位為rad/s(弧度/秒)。 它與正弦量的周期和頻率f之間的關系為:
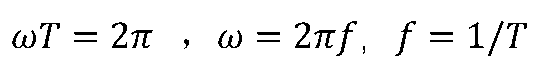
頻率f的單位為1/s(1/秒),稱為Hz(赫茲,簡稱赫)。
?i是正弦量在t=0時刻的相位,稱為正弦量的初相位(角),簡稱初相,即
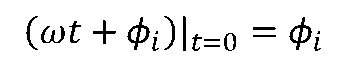
初相的單位用弧度或度表示,通常在主值范圍內取值,即|?i|≤180°。 初相與計時零點的選擇有關。
對于同一電路系統中的許多相關的正弦量,只能相對于一個共同的計時零點確定各自的相位。
正弦量的三要素是正弦量之間進行比較和區分的依據。
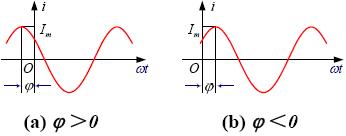
正弦量隨時間的變化的圖形稱為正弦波。 下圖為正弦電流i的波形圖(?i>0),橫軸可以用時間t或wt(rad)兩種方式表示。
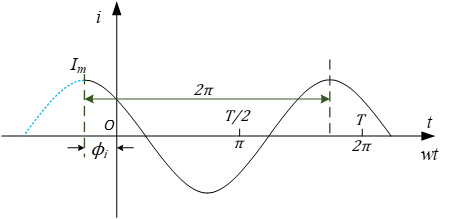
正弦量乘以常數,正弦量的微分、積分,同頻正弦量的代數和等運算,其結果仍為一個同頻率的正弦量。
工程中常將周期電流或電壓在一個周期內產生的平均效應換算為等效的直流量,以衡量和比較周期電流或電壓的效應,這一等效的直流量就稱為周期量的有效值,用相應大寫字母表示。
如周期量i的有效值I定義如下:
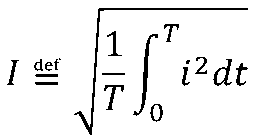
即周期量的有效值等于其瞬時值的平方在一個周期內積分的平均值的平方根,因此有效值也稱均方根值。
有效值和峰值的關系:
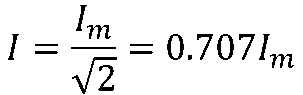
兩個同頻正弦量的相位差等于它們相位相減的結果。
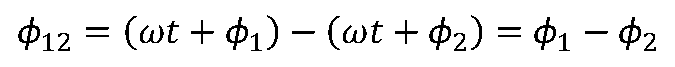
同頻正弦量的相位差等于初相位之差,是一個與時間無關的常數。 電路中常用“超前”和“滯后”來表示兩個正弦量之間的相位關系。
當?12>0時,稱為1超前2,或2滯后于1; 當?12=0時,稱為1和2同相;|?12|=π/2時,稱1和2相交;|?12|=π時,稱1和2反相。
03 相量法的基礎
相量法是分析正弦電路穩定狀態的一種簡易方法。
根據電路定律VCR、KCL和KVL,編寫含有儲能元件的線性非時變電路的電路方程,如下所示。
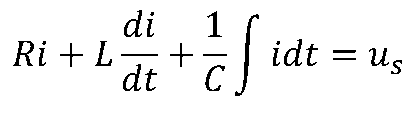
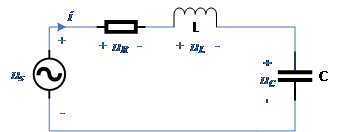
當us為正弦量時,上述方程中的電流i的特解(響應的強制分量)一定是與us同一頻率的正弦量。 即線性非時變電路在正弦電源激勵下,各支路電壓、電流的特解都是與激勵同頻率的正弦量,當電路中存在有多個同頻率的正弦激勵時,該結論同樣成立。
工程中將電路的這一特解狀態稱為正弦電路的穩定狀態,簡稱正弦穩態。 電路處于正弦穩態時,同頻率的各正弦量之間,僅在有效值、初相上存在“差異和聯系”。
電路中正弦電壓us和正弦電流i對應的向量可以表示為:
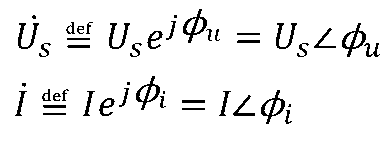
即正弦量的對應相量是一個復數,它的模為正弦量的有效值,它的輻角為正弦量的初相。
相量在復平面上表示的圖形稱為相量圖,如下圖所示。

電路中有時也用正弦量的振幅表示相量的模,稱為振幅相量。
04 電路定律的相量形式
用相量通過復數形式的電路方程描述電路的基本定律VCR(電壓、電流和電阻關系)、KCL(基爾霍夫電流定律)和KVL(基爾霍夫電壓定律),稱為電路定律的相量形式。
注:電路的運行規則由電路的結構和元件的特性共同決定,KCL和KVL描述電路結構,VCR描述元件特性。
KCL的相量形式:
對電路中任一節點有:
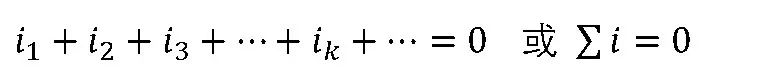
當式中的電流全部都是同頻率的正弦量時,則可變換為相量形式為:
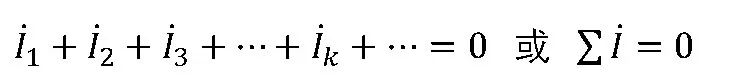
即任一節點上同頻率的正弦電流的對應相量的代數和為零。
KVL的相量形式:
對電路中任一回路有:
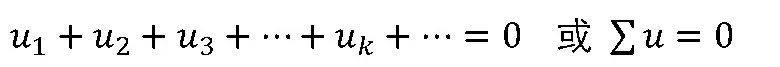
即任一結點上同頻的正弦電流的對應相量的代數和為零。
當式中的電壓全都是同頻的正弦量時,可變換稱相量形式為:
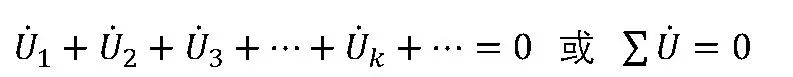
即任一回路中同頻的正弦電壓的對應相量的代數和為零。
電阻、電感和電容元件的VCR的相量形式:當有正弦電流
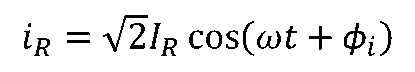
通過時,根據歐姆定律,電壓-電流的時域關系為
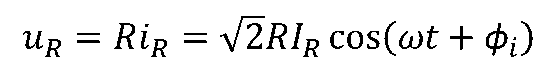
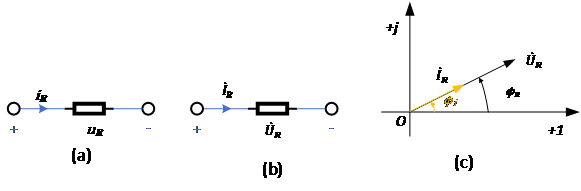
說明電阻上的電壓、電流都是同頻的正弦量。 令電壓相量為
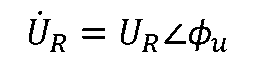
,則相量形式有
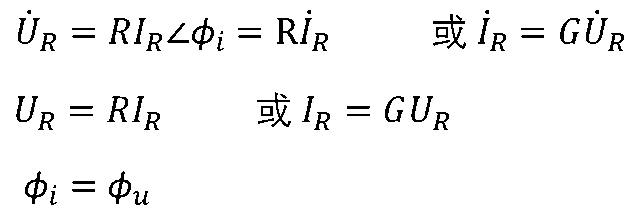
他們的有效值依然符合歐姆定律,輻角相等,即電壓電流同相。
若是電感電路中,有正弦電流
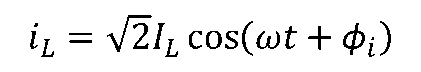
通過時,根據電感的電壓-電流的時域關系有
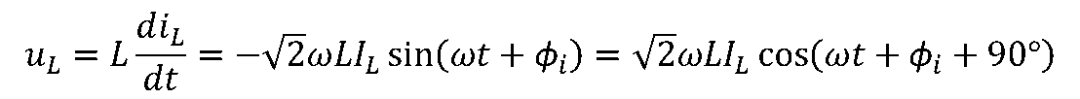
說明電感L上的電壓、電流為同頻正弦量。 令電壓相量為
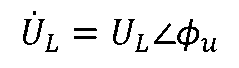
,uL的表達式變換后的相量形式為
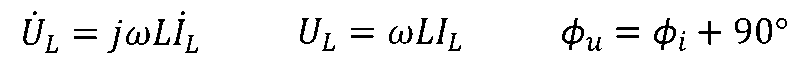

電壓、電流有效值之間的關系類似于歐姆定律,但與角頻率ω有關,其中與頻率成正比的ωL具有與電阻相同的量綱[Ω],稱為感抗, -1/ωL稱為感納;
電感L上的電壓將跟隨頻率變化,當ω=0時(直流), ωL=0,uL=0,電感相當于短路; 當ω=∞時,
ωLà∞,i=0,電感相當于k開路,在相位上電壓超前電流90°。
對于電容電路而言,有和電感相似的特性,只不過剛好相反。
其結論如下:
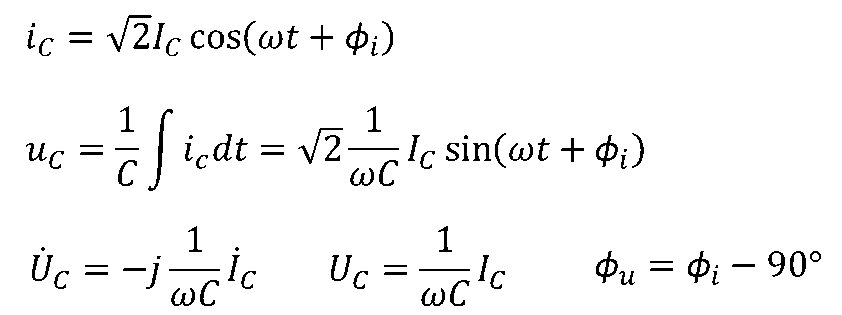
電壓、電流有效值之間的關系類似于歐姆定律,但與角頻率ω有關,其中與頻率成正比的-1/ωC具有與電阻相同的量綱[Ω],稱為容抗,ωC稱為容納;
電容C上的電壓將跟隨頻率變化,當ω=0時(直流),1/ωC =∞,iC=0,電容相當于開路; 當ω=∞時,1/ωC à0,
uL=0,電容相當于短路,在相位上電壓滯后電流90°。
-
電流
+關注
關注
40文章
7095瀏覽量
133840 -
穩態分析
+關注
關注
0文章
9瀏覽量
6604 -
線性電路
+關注
關注
0文章
61瀏覽量
12465 -
相量法
+關注
關注
0文章
5瀏覽量
6740 -
正弦穩態
+關注
關注
0文章
2瀏覽量
5197
發布評論請先 登錄





 線性電路正弦穩態分析方法之相量法
線性電路正弦穩態分析方法之相量法












評論