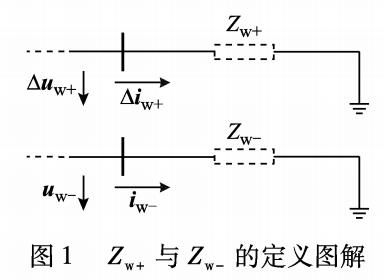
正弦電路中有時也會碰到無限電路的情況,比如電力輸電線路,可以取單位長度為基本單元,長度理想化成無限長,從而構成單元長度重復無窮次的無限電路。 此類電路的求解可以根據其重復性列方程。
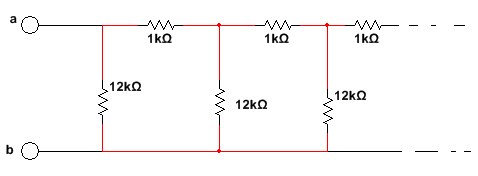
例:圖1所示電路為一無限梯形網絡,外加電壓:
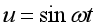
V,求當
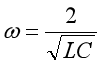
時,該網絡的等效復阻抗。
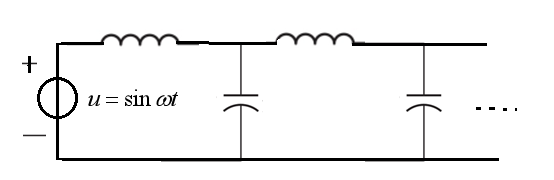
圖1 原電路
分析:該電路為無限梯形網絡,網絡由圖2所示基本單元鏈接而成,輸入阻抗具有重復性:增加一個單元或減少一個單元,不影響電路的輸入阻抗。
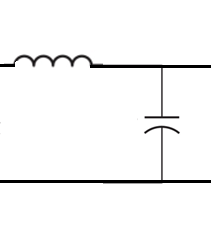
圖2電路單元
由此可列方程:假設網絡N的等效阻抗為Z,可得:
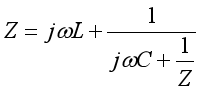
將上方程恒等變形,可得:
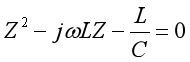
解此方程,可得:
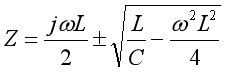
當
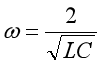
時,
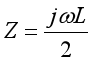
由此可得,該無限梯形網絡的等效阻抗為
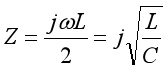
為純電感。
同理,交換圖1 所示電路中電感和電容的位置,也可以證明,當
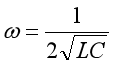
時,

為純電容。
綜上,無限電路的等效阻抗求解,關鍵是找出重復單元,利用增減一個單元不影響電路等效阻抗列方程求解。
-
電路
+關注
關注
173文章
6024瀏覽量
174747 -
電容
+關注
關注
100文章
6242瀏覽量
153711 -
電感
+關注
關注
54文章
6197瀏覽量
103940 -
正弦電路
+關注
關注
0文章
10瀏覽量
7464 -
等效阻抗
+關注
關注
0文章
7瀏覽量
3294
發布評論請先 登錄
阻抗變換是不是等效變換?
穩恒電路的等效化簡
正弦交流電路的阻抗、導納及等效轉換
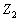
撬棒保護的DFIG等效序阻抗





 無限電路的等效阻抗求解
無限電路的等效阻抗求解












評論