Ising模型與QUBO模型

1.伊辛模型(Ising Model)

相干伊辛機(Coherent Ising Machine, 簡稱CIM), 是目前玻色量子重點研發的一項光量子計算機技術，CIM是一種基于簡并光學參量振蕩器(DOPO)的光量子計算機，在數學實踐中, 我們可以將其抽象為優化Ising模型的專用計算機。

Ising模型是一類描述物質相變的隨機過程模型。抽象為數學形式為：

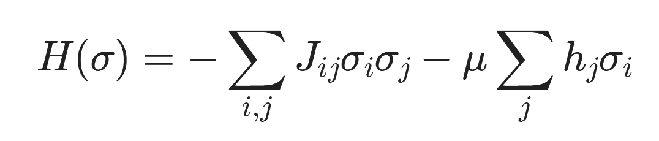
其中σ為待求自旋變量, 取值為{+1，-1}，H為哈密頓量，J和μ分別為二次項系數、線性項系數, 是已知量。

2.區分

QUBO模型更便于建模，Ising模型可以用于CIM求解器直接求解。同時，QUBO模型和Ising模型之間可以互相轉化。

1）變量代換

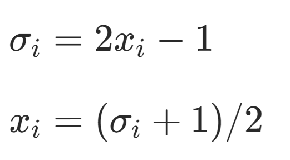
2）創建輔助變量完成一次項轉化

QUBO模型建模秘籍

一、什么是組合優化問題？

組合優化(Combinatorial Optimization, CO)領域是優化領域中最重要的領域之一，它也是運籌學、計算機科學和分析學研究團體所追求的最活躍的研究領域之一。

組合優化是在一個有限的對象集中找出最優對象的一類問題。組合優化的問題特征是可行解的集是離散或者可以簡化到離散的，目標是找到最優解。常見的例子有數字劃分問題、旅行商問題等。

一般來說，這些問題涉及在必須做出大量是/否決策的情況下做出明智的選擇，并且每一組決策都會產生相應的目標函數值，例如成本或利潤值。然而在這些環境中找到好的解決方案是極其困難的。

而QUBO建模方式可以包含在工業、科學和政府中發現的各種重要CO問題，借助QUBO求解器的求解能力可以有效地幫助解決許多重要問題。

二、什么是QUBO模型？

QUBO（QuadraticUnconstrained Binary Optimizatoin），無約束二次二進制優化模型是現在量子計算中應用最廣泛的優化模型，它統一了豐富多樣的組合優化問題。

隨著問題規模的增加，利用傳統方法求解該問題，求解時間會變得不可接受，但利用QUBO模型可以通過量子計算機加速，高效求解組合優化問題。同時，QUBO模型可以表達位運算，進而表達各種邏輯，操作簡便，具體形式如下。

1.基礎QUBO形式：minimize/maximize

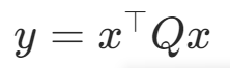
Q為QUBO矩陣，x為二進制變量組成的向量，每個變量取值均為{0,1}，QUBO目標為找到使得y最小或最大的x

其中，Q矩陣的形式有2種：

1）對稱形式

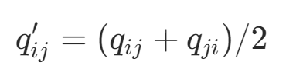
2）上三角形式

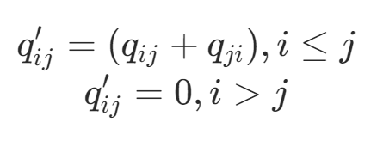
舉例：

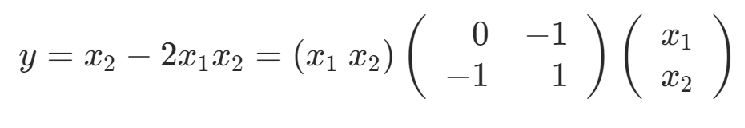
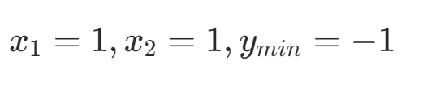
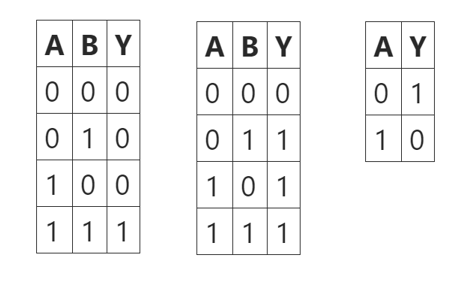
2.位運算

與 同時為1，結果才為1；

或 同時為0，結果才為0；

非0變成1，1變成0；

異或 兩位相同為0，相異為1

位運算表達

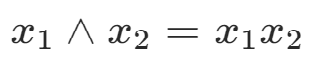
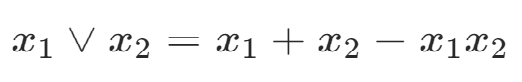
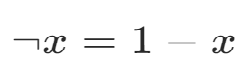
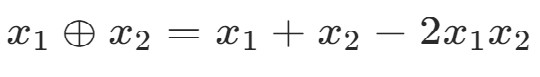
3.添加約束條件

舉例1：

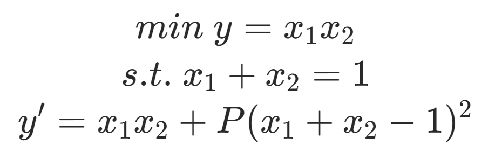
通過添加約束項，并設置較大的系數P保證約束內容的優先級。

舉例2：

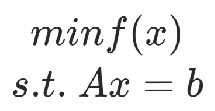
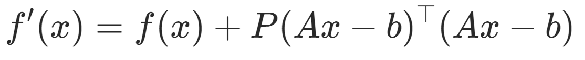
約束條件舉例

? ? ?

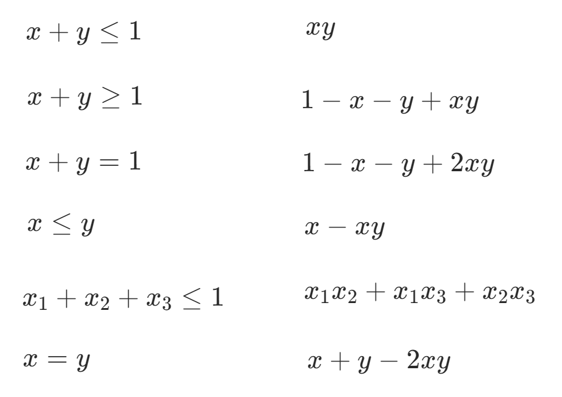4.整數表達

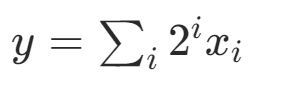
通過二進制表達整數，使用d個變量可以表達0到2^d ?1 的數字。

舉例：

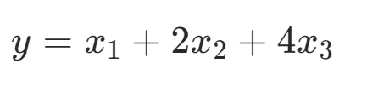
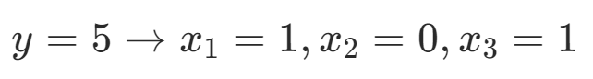
5.不等式約束

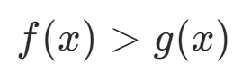
不等式約束可以轉化為等式約束，通過松弛變量y表示出不等式兩邊的差。

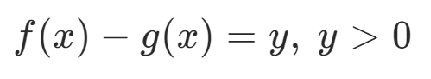
其中y為通過二進制表達的整數，構造約束項：

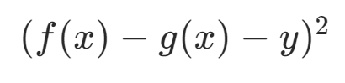
（注意點：這樣做會引入新的變量，增加問題規模）

6.擴展思考

HOBO問題（High Order Binary Optimization），是指用二次多項式難以表達的高次問題。對于高次的問題，可以將x1x2替換為y，并添加約束項使得x1x2=y，從而將高次的問題轉化為二次優化問題。

約束項：Rosenberg多項式

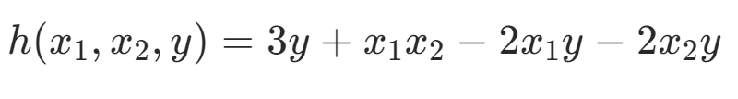
滿足：

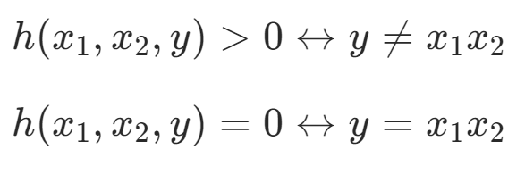
（注意點：這樣做會引入新的變量，增加問題規模）

三、QUBO可以解決哪些問題？

最大獨立集問題

不對稱分配問題

對稱分配問題

邊約束分配問題

二次背包問題

最大團問題

最大割問題

整數劃分問題

旅行商問題

舉例1：整數劃分問題

1）整數劃分問題（The Number Partitioning Problem），NP-complete將包含n個非負整數的數集劃分為兩個子集，使這兩個子集的和盡可能接近

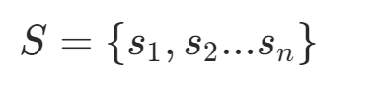
設數集為

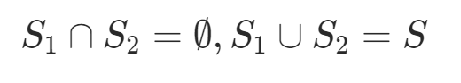
選兩個子集滿足，使得下值最小

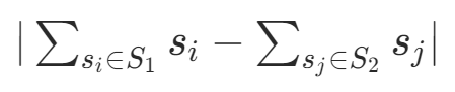
舉例S= {1，2，3，4，8}，一組最有解為S1= {1,8} S2={2,3,4}是一組最優解，兩者的和均為9

2）整數劃分問題建模思路

1. 定義決策變量，決定每個整數被分到哪一個集合

2. 使用決策變量表達出兩個集合整數和的差值

3. 通過CIM優化目標函數，得到最小值對應的解

3）整數劃分問題建模過程

定義決策變量xi，xi=1表示 Si∈S1，xi=0表示Si∈S2

兩個子集求和的差值：

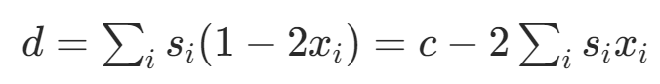
目標函數：

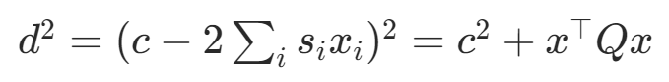
其中，

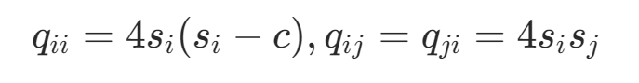
舉例2：旅行商問題

1）旅行商問題（Traveling Salesman Problem）NP-Complete，商人想要在地圖上走完所有城市，每個城市只經過一次，最后回到最初的城市，求路程最短的走法。

給定帶權圖G(V,E)，V為點集，E為邊集，要求遍歷所有點再回到初始點，求路程最短的走法。哈密頓回路：遍歷所有點再回到初始點。

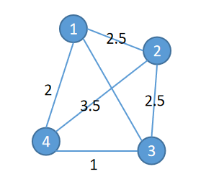
舉例：

2）旅行商問題建模思路1.0

以下圖為例，定義決策變量xi,u，表示“經過的第i個節點為u”是否為真，通過決策變量表達出距離，再通過添加約束條件使得求解方案能夠成立，構造得到表達式通過CIM進行優化。

目標包括：

1. 路程最小

2. 路線為環（約束自然滿足）

3. 同時只能經過一個節點（約束）

4. 每個點經過次數為1（約束）

5. 不能走不存在的連接（約束）

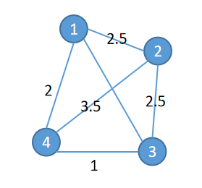
3）旅行商問題建模過程

設有n個節點，wu,v從u到v的邊的邊權，定義決策變量xi,u，表示“經過的第i個節點為u”是否為真，路程為環可以根據決策變量的定義自然滿足，則經過的路程可以表達為：

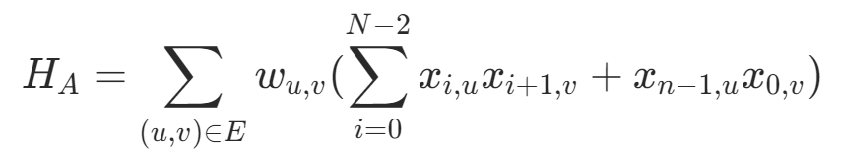
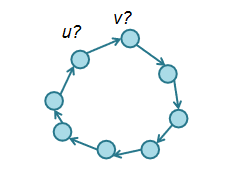
4）旅行商問題約束條件

為使得xi,u符合實際情況，需要如下約束：

第i個節點只有一個節點

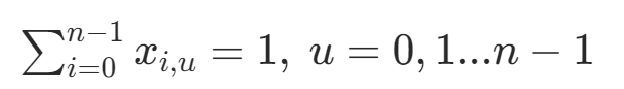
節點u只在路線中出現一次

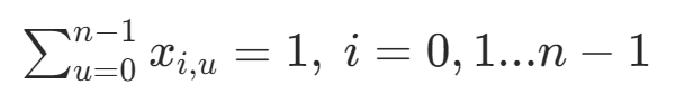
可以根據以上兩個條件構造約束

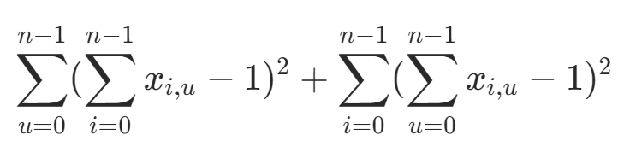
為了保證不存在的邊不出現在方案中設置約束項

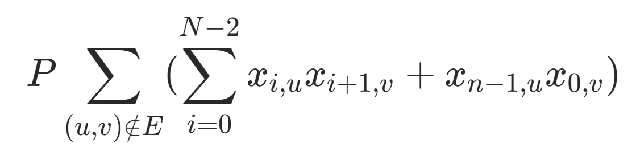
P為懲罰項系數，取值需要顯著大于其他邊權，最終的約束項：

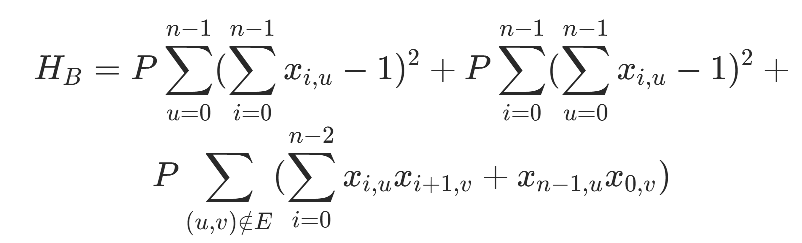
目標函數包括回路總長和約束兩部分：

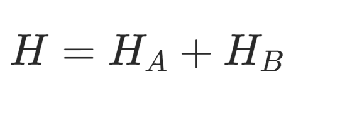
2）旅行商問題建模思路2.0

定義決策變量xu,v，表示“使用u到v的邊”，通過決策變量表達出距離，再通過添加約束條件使得求解方案能夠成立，構造得到表達式通過CIM進行優化。

目標包括：

1. 路程最小

2. 每個點出發一次（約束）

3. 到達每個點一次（約束）

4. 不能走不存在的連接（約束）

由于相干光量子計算最擅長攻克組合優化問題，可應用賦能場景廣泛，如金融業的投資組合優化、資本風險分析建模；生物制藥業的蛋白質折疊、小分子組合和DNA重組；

交通物流行業路徑優化等，這些都是在實際工作中經常遇見的復雜度很高且計算量巨大的常規問題，所以該技術路線高度貼合市場需求，普適率高。

審核編輯：劉清