寫在前面
本文是本系列的第一篇,參考杜勇老師的數字濾波器MATLAB和Verilog實現以及一些網文博客,更新順序參考杜勇老師的書籍目錄。 本文主要介紹關于數字信號的一些基礎知識。
固定點數
數字既包括整數,又包括小數,而小數的精度范圍要比整數大得多,所以如果我們想在計算機中,既能表示整數,也能表示小數,關鍵就在于這個小數點如何表示。 于是人們想出一種方法,即 約定計算機中小數點的位置 ,且這個位置固定不變,小數點前、后的數字,分別用二進制表示,然后組合起來就可以把這個數字在計算機中存儲起來,這種表示方式叫做「定點」表示法,用這種方法表示的數字叫做「定點數」。 也就是說「定」是指固定的意思,「點」是指小數點,小數點位置固定即定點數名字的由來。
在計算機中,通常將數據的小數點固定在數據的最高位之前或者最低位之后。 前者稱為定點小數,后者稱為定點整數。 定點小數 是純小數,約定的小數點位置在符號位之后、有效數值部分最高位之前。 若數據 x 的形式為 x = x0.x1x2… xn ( 其中x0為符號位,x1~xn是數值的有效部分,也稱為尾數, x1為最高有效位 ),則在計算機中的表示形式為:

在數字處理中,定點數通常把數限制-1~ 1之間,把小數點規定在符號位和數據位之間,而把整數位作為符號位,用0 、1表示正負,數本身只有小數部分,即尾數。 這是由于經過定點數的乘法后,所得的結果小數點位置不確定,除非兩個乘數都是小數或者整數。 對于加法來說,小數點的位置是固定的,如上圖x0位符號位,x1~xn為數據位。 在整個運算過程中,要求所有的運算結果的絕對值都不能超過1,否則會出現溢出。 在實際問題中,處理運算的中間過程會可能會出現結果超過1的情況,為了使得運算正確,通常會在運算時乘一個比例因子(類似歸一化)避免發生溢出現象。
定點數的三種表示方法
定點帶符號數在計算機內的四種表示方法是: 原碼,補碼,反碼。 在FPGA處理中,比較都常用。
原碼表示
最高位為符號位,0表示正數,1表示負數,其余位是數值位。 原碼的優點是簡單直觀,特點是符號位與數值位在運算時要區別對待。 0的原碼表示有兩種形式。
反碼表示
正數的反碼表示與原碼表示一樣; 負數的反碼表示為該負數對應的原碼符號位不變,數值位按位取反。 因此,在反碼表示中,最高位還是符號位,0表示正,1表示負,與原碼相同。 0的反碼表示也有兩種形式。
補碼表示
正數的補碼表示與原碼表示相同; 負數的補碼表示是原碼表示的符號位不變數值位取反,并在最低位加1。 補碼中0的表示是唯一的。
浮點數
浮點數是一種公式化的表達方式,用來近似表示實數,并且可以在表達范圍和表示精度之間進行權衡(因此被稱為浮點數)。 在計算機中可以近似表達任意實數。 浮點數通常被表示為:A=M×B^E,B被稱為階碼的基數,精度為N(使用多少位來進行存儲),E在浮點數中表示為基的指數。 M被稱為浮點數的尾數。
浮點顯示方法
要表示浮點數,一是要給出尾數M的值,通常用定點小數形式表示,它決定了浮點數的表示精度,即可以給出的有效數字的位數。 二是要給出階碼,通常用定點整數形式表示,它指出的是小數點在數據中的位置,決定了浮點數的表示范圍。 因此,在計算機中,浮點數通常被表示成如下格式:(假定為32位浮點數,基為2,其中最高位為符號位)
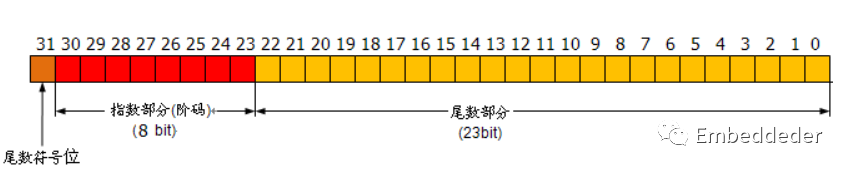
一種FPGA處理浮點數格式
雖然浮點數的表示范圍更大,但實現時消耗的資源更多,實現的步驟也更加繁瑣。 如浮點數的加法需要以下步驟:
- 對階操作:比較指數的大小,對指數小的操作數進行移位,完成尾數的對階操作。
- 尾數相加:對階后的尾數進行加減操作。
- 規格化:規格化有效位并根據移位方向和位數修改最終的階數。
浮點數乘法操作,一般需要以下操作:
- 指數相加:完成兩個操作數的指數相加運算。
- 尾數調整:將尾數M調整為1.M的補碼格式。
- 尾數相乘:完成講個操作數的尾數相乘運算。
- 規格化:根據尾數運算結果調整指數位,并對尾數進行舍入截位操作,規格化輸出結果。
浮點數乘法器的運算速度主要由FPGA內部集成的硬件乘法器決定。 大部分FPGA芯片內部的乘法器為18bitX18bit。 這里以7系列的xilinx為例。 DSP48內部的乘法器為25X18的,如下圖:
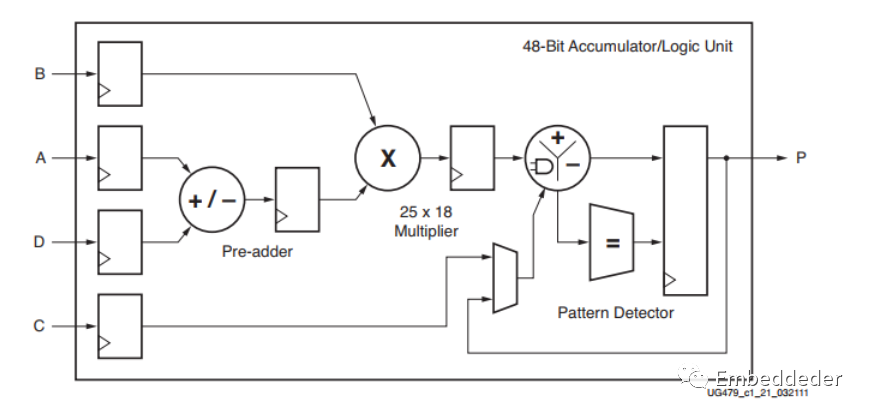
如果進行24位的乘法運算,則需要使用4個18bitX18bit乘法器,兩個18位的數乘法操作只占用一個18bitX18bit乘法器。 由于FPGA的寄存器資源的設計,可以直接將尾數表示為補碼的格式。 可以去除尾數調整的運算,減少一級流水操作。
杜勇老師在他的《多輸入浮點加法器算法研究》中提出了一種新的浮點數結格式,也即一個26位寬的數,25--18位表示為8位有符號數,17--0表示為18位有符號的小數。 浮點數的表示式為M = f X 2^e;

規定,數值1的表示方法為指數為0,尾數為01_1111_1111_1111_1111;數值0表示為指數為-128,尾數為0。 這種自定義浮點數格式,相比24位的普通浮點數運算雖然精度有所下降但是可以大大節省乘法器的資源由是個乘法器變為1個,并有效地減少了運算步驟,提高了運算速率(由二級18X18乘法運算減少到一級運算)。
自定義浮點數和實數之間的關系:

FPGA中的運算
加減法運算
小數加減法運算
在Verilog中比較常用的數據類型是wire和reg以及他們的向量形式,在Verilog中,默認將所有的二進制數當做小數處理,也就是說小數點均在最低位的右邊。 帶小數的運算,設計者可以通過隱形規定進行,如,假設規定一個小數運算的小數點在最高位和次高位之間,然后進行小數的加減法運算。 和十進制的運算規則相同,在做加減法運算時,參與運算的兩個數的小數點必須對齊,并且結果的小數點位置相同。
還有一種比較常用的處理辦法是,將小數轉換為整數進行運算,處理過程為同時把要運算的數進行乘一個很大的數如1024,即乘一個很大的整數處理掉小數部分,轉化為整數,并約定該整數為之前的小數。 但是這樣處理的弊端也比較明顯,相比于直接進行隱形規定小數運算,會消耗更多的資源。
負數加減法
Verilog默認狀態都表示的是無符號數,如果要指定某個數為有符號數,要在聲明前加入關鍵字signed,如:wire signed [2:0] data; 這里表示data為3bit的有符號數,在運算時自動采用有符號運算。 下面引用杜勇老師書上的一個示例,并做略微改動。
有無符號數對比示例:
源文件:
`timescale 1ns / 1ps
module adder_test(
data1,
data2,
sum_signed_out,
sum_unsigned_out,
compare_signed,
compare_unsigned);
input [3:0]data1; //輸入加數1
input [3:0]data2; //輸入加數2
output [3:0] sum_unsigned_out; //無符號加法輸出
outputsigned [3:0] sum_signed_out; //有符號加法輸出
output [3:0] compare_signed; //有符號數比較輸出
output [3:0] compare_unsigned; //無符號數比較輸出
//無符號加法運算
assign sum_unsigned_out = data1 + data2;
//有符號加法運算
wiresigned [3:0] s_data1;
wiresigned [3:0] s_data2;
assign s_data1 = data1;
assign s_data2 = data2;
assign sum_signed_out = s_data1 + s_data2;
//比較操作
wiresigned [3:0] cons_1 = 4'b1001;
assign compare_signed = (sum_signed_out < cons_1)? 1 : 0;
assign compare_unsigned = (sum_unsigned_out < cons_1)? 1 : 0;
endmodule
測試文件:
`timescale 1ns / 1ps
module tb_adder();
//輸入
reg [3:0] data1;
reg [3:0] data2;
//輸出
wire [3:0] sum_unsigned_out;
wire [3:0] sum_signed_out ;
wire compare_signed ;
wire compare_unsigned;
//例化
adder_test u_adder_test(
.data1 (data1 ),
.data2 (data2 ),
.sum_unsigned_out (sum_unsigned_out ),
.sum_signed_out (sum_signed_out ),
.compare_signed (compare_signed ),
.compare_unsigned (compare_unsigned )
);
//測試
initialbegin
data1 = 0;
data2 = 0;
repeat(16)begin
data1 = data1 + 1;
data2 = data2 + 1;
#20;
end
end
endmodule
綜合的RTL圖:
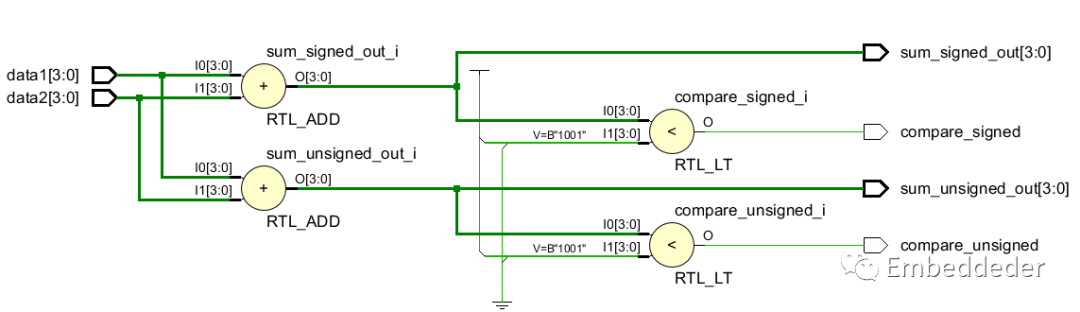
此時的仿真結果為下圖:
通過對比可以知道,在進行運算時,有無符號數的運算結果在二進制中查看是相同的,但是表達的數值大小有區別,除此之外,有無符號數的區別也體現在比較運算上。

從下圖中,可以看出,對于有無符號數來說,4‘b1001有符號數對應的是-7,無符號數對應的是9,所以兩者的結果是不一樣的。
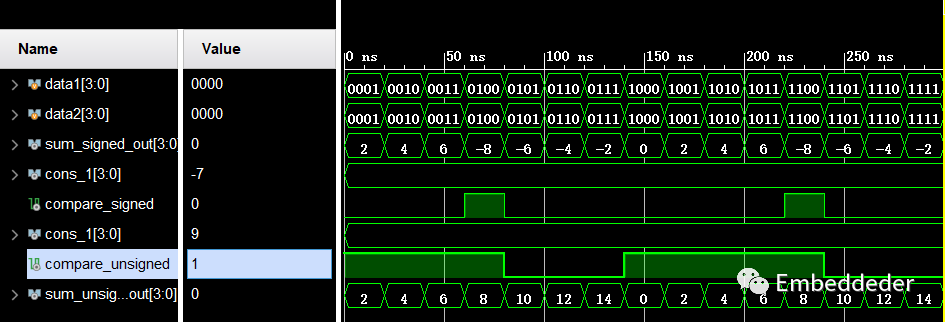
比較操作中為何不直接使用(sum_signed_out < 4'b1001)?
這里作為對比,將比較操作語句的cons_1直接改為4'b1001;
//比較操作
//wire signed [3:0] cons_1 = 4'b1001;
assign compare_signed = (sum_signed_out < 4'b1001)? 1 : 0;
assign compare_unsigned = (sum_unsigned_out < 4'b1001)? 1 : 0;
在vivado的編譯仿真器環境下輸出結果如下:
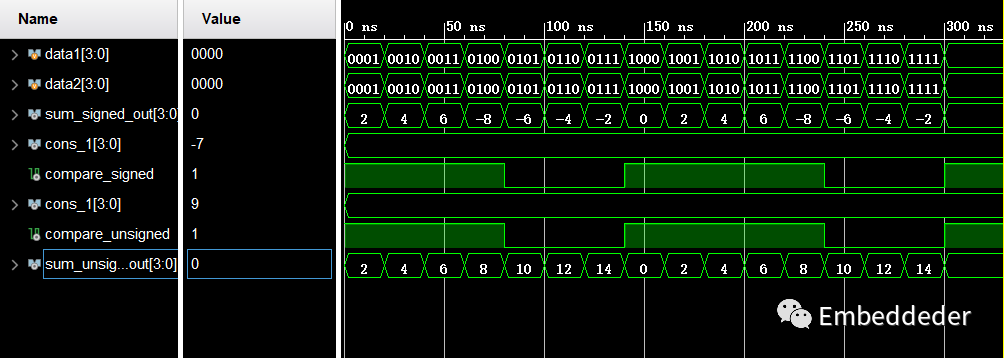
從波形可以看出,兩個比較操作都是按照無符號數進行比較,這是因為在進行比較操作時,直接把比較數寫入4'b1001,編譯器會默認該數為無符號數,比較會按照無符號進行比較輸出。 所以**有符號數進行比較時加上signed,即可考慮數值正負,完成正確比較,必須兩個都要加signed,否則當作無符號進行比較。 否則只會將有符號數看作無符號數進行比較。 **
乘法運算
對于乘法運算,可以選擇使用工具中自帶的IP核,也可以使用基本的組件進行設計乘法電路。 相比加減法,乘法電路更消耗資源,一般情況下,對于信號和信號(數據)之間的運算,通常調用IP進行實現,而常數和信號直接的乘法運算,可以通過進行移位和加減法實現。 例如一個數乘2,等效為這個數左移一位; 一個數乘3等效為這個數左移一位+該數本身。
因為乘法運算的結果數據位數比乘數位數多,所以在實現乘法時,要先進行數據位數是擴展,以免出現數據溢出的現象。
除法運算
和乘法類似,可以選擇使用工具中自帶的IP核實現除法電路。 但是除法不可以在Verilog程序中進行直接實現,類比乘法電路的實現方法,可以將除法進行分解成若干右移的小項,然后進行加減運算操作。 例如一個數除以2,則可以將該數進行右移一位; 一個數除以3,可以將該數(記該數為A)近似分解 為,A右移2位+A右移4位+A右移6位。 (相當于該數乘了0.3281),因為該數是無限小數,所以對于分解法只能得到近似的結果,分解的項數越多,精度越高。 因為FPGA這些數字信號處理平臺不可避免有限字長效應引起的。
有效數據位的計算
在FPGA中,所有的數據都是通過寄存器來存儲,使用的寄存器越多,消耗的資源也就越多。 所以為了保證硬件資源的有效利用,需要精準掌握運算中的有效數據位的長度,盡可能的減少無效數據位參與運算,浪費資源。 有效數據位表示有用的數據位,例如數據范圍為0-9,從寄存器的角度來說,只需要4個寄存器進行存儲即可枚舉所有0-9的狀態,如果此時定義了5位的寄存器向量,那么多出來的那一位是無效的,任何時候都不代表任何信息。
加法運算的有效數據位
對于整數加法來說,假設加法中的兩個加數最大的位數為N,則加法運算結果需要N+1位 才能保證結果不溢出。
對于小數加法來說,如果采用N+1位的數據表示運算結果,則小數點的位置在數據次高位的右邊,如果采用N位數據表示運算結果,則小數點的位置在數據最高位的右邊。 簡而言之就是,小數部分的數據位數是不變的 。 為了確保得到N+1位的準確結果,要對參加運算的兩個數進行一位符號位的拓展 。
乘法運算的有效數據位
對于數據長為M和N的數據進行乘法運算時,需要M+N位的數據才能得到準確的結果。 對于乘法運算當乘數為小數時,,不需要通過拓展位數類對齊乘數的小數點位置,乘法的結果的小數位數等于兩個乘數的小數位數之和。 對乘法進行截取時,為了保證結果正確,只能取高位,舍棄低位。 只有在兩個乘數均能表示最小負數時,才能拿出現最高位和次高位不同情況。 (最高位為1,其余為0),只有在這種情況下需要M+N位的數來存放結果,其他情況下,只需要M+N-1位來存放結果。
乘加法運算的有效數據位
在數字信號處理中,通常會遇到乘加運算的情況,一個典型的例子就是有限脈沖響應(Finite Impulse Response,FIR)濾波器的設計。 當乘法系數是常量時,最終運算結果的有效數據數據位根據常量的大小來重新計算。 假設乘加運算的變量輸入是N位的數據,乘加運算的輸出有效數據位計算如下:計算所有常數乘數絕對值之和SUM,算出SUM所占用的二進制數據位n,則乘加運算的輸出的有效數據位數為N+n。
有限字長效應
數字信號處理的實質是一組數值運算,這些運算可以在計算機上用軟件實現,也可以用專門的硬件實現。 無論哪種實現方式,數字信號處理系統的一些系數、信號序列的各個數值及運算結果都要以二進制形式存儲在有限字長的存儲單元中。 如果存儲的是模擬信號,例如常用的采樣信號處理系統,輸入的模擬量經過采樣和模數轉換后,變成有限長的數字信號。 有限長的數就是有限精度的數。 因此,具體實現中往往難以保證原設計精度而產生誤差,甚至導致錯誤的結果。 在數字系統中主要有三種因有限字長而引起誤差的因素:
- 模數轉換器把模擬輸入信號轉換為數字信號時產生的量化效應
- 把系數用有限位二進制表示時產生的量化效應
- 數字運算過程中,為限制位數進行的位數處理和為防止溢出而壓縮信號電平的有限字長效應
引起這些誤差的根本原因在于寄存器(存儲單元)的字長有限。 誤差的特性與系統的類型、結構形式、數字的表示法、運算方式及字的長短有關。 在通用計算機上,字長較長,量化步很小,量化誤差不大。 但在專用硬件,如FPGA,實現數字系統時,其字長較短,就必須考慮有限字長效應了。
-
matlab
+關注
關注
188文章
2998瀏覽量
233393 -
數字濾波器
+關注
關注
4文章
272瀏覽量
47521 -
計算機
+關注
關注
19文章
7636瀏覽量
90284 -
數字信號處理
+關注
關注
16文章
567瀏覽量
46578 -
Verilog
+關注
關注
29文章
1366瀏覽量
111918
發布評論請先 登錄
進群免費領FPGA學習資料!數字信號處理、傅里葉變換與FPGA開發等
電信系統的數字信號基礎知識
數字信號處理基礎知識
數字信號處理基礎知識PPT課件
數字信號處理和DSP架構的基礎知識及系列產品分析
智能手環之技術應用FFT的C程序





 數字信號處理的基礎知識
數字信號處理的基礎知識











評論