A.什么是高、低頻信號？

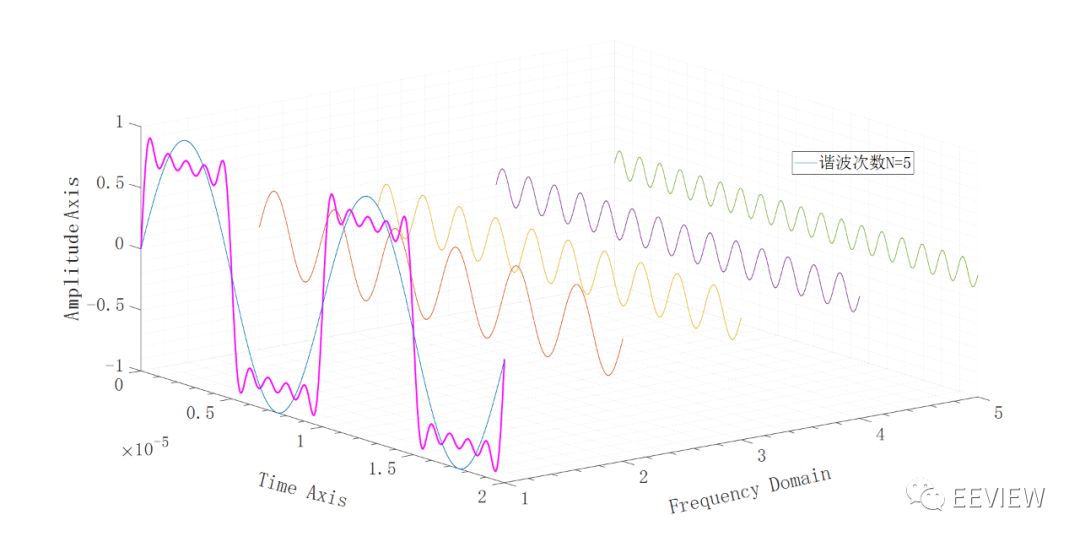
1.高頻信號在信號的頻譜特性上占據了（處于）Frequency Domain較高的段。

2.低頻信號在信號的頻譜特性上占據了（處于）Frequency Domain較低的段。

3.通常用于測試的是正弦信號（原因是頻譜純凈）

4.時域是真實世界唯一存在的域，頻域是抽象的，是一種遵循特定規則的數學范疇，是用來幫助理解時域的。

5.時域中描述一個正弦，需要以下幾個參量：幅度、頻率、相位（多數時

候不考慮）。在頻域中，需要的參量急劇減少：在某頻率處的一個有高度的點、相位（多數時候不考慮）。時域中，由上述三個參量構成的成百上千的點，在頻域只表現一個點。

對于一個正弦波，其頻譜就是周期的倒數，所以正弦信號是“最干凈”的信號，通常也用于信號激勵用于測試。

正弦信號：表現在頻域上只有在正頻域處只有w0處對應的一個沖激函

數，頻譜十分純凈。

方波信號：一個1Hz極慢的方波信號只要上升沿足夠陡峭，其所帶的高

頻分量也是極多的，因為方波信號的頻譜包含基波，以及它的高次諧波，直至頻率彌散至無窮大，幅度遞減。（直觀的傅里葉級數表現為：需要用很多頻率更高的正弦，才能疊出來陡峭的上升沿）如下圖所示，100Khz的方波信號需要由其基頻100K，由于其是奇諧函數，頻譜特點是，1,3,5,7,9…倍的基頻出現在頻譜上。

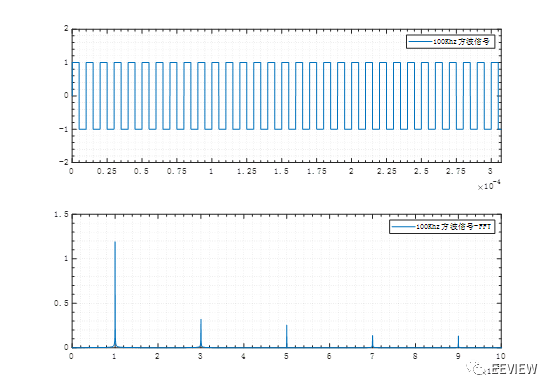
圖 1?1方波信號的FFT

B.高頻信號混入低頻噪聲小信號時頻表現

下圖所示為3Mhz正弦混入20Khz小信號正弦，在時域上，由于時間比較長，所以只能看出來是一塊波形，放大打開可以看到高頻的正弦信號。注意：低頻的小信號噪聲疊加在高頻的大信號，時域上需要看其包絡變化，對應示波器中需要擴大時基，屏幕上觀察更多的信號。

為什么低頻的信號表現在時域上是在包絡上，原因是：1.假設只有30Mhz的正弦，那么在很長的時間區間上，我們只能看到一塊標準的長方形，幅值都在±1V。2.此時此刻疊加一個低頻正弦信號，那么在很大的時間區間上某些點處幅值會降低，某些點處幅值會增高，由于其周期長（低頻），所以它的包絡就是所加的低頻信號的周期，對于正弦噪聲即頻率。

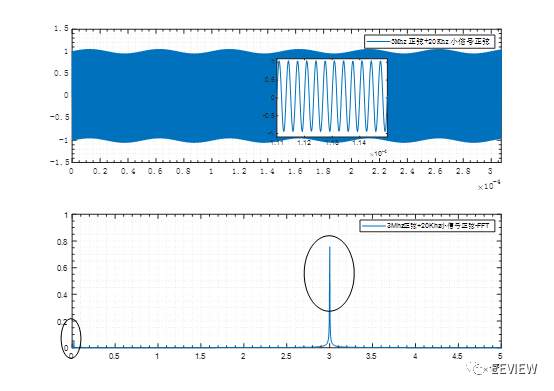
圖 2?1 3Mhz正弦混入20Khz小信號正弦

f1=0.02*1e6;f2=3*1e6;

y1=0.05sin(2pif1t)+1sin(2pif2t);

通過FFT可以看到低頻的小信號噪聲幅值比較小，這種低頻的小信號噪聲，表現在時域上是包絡變化。

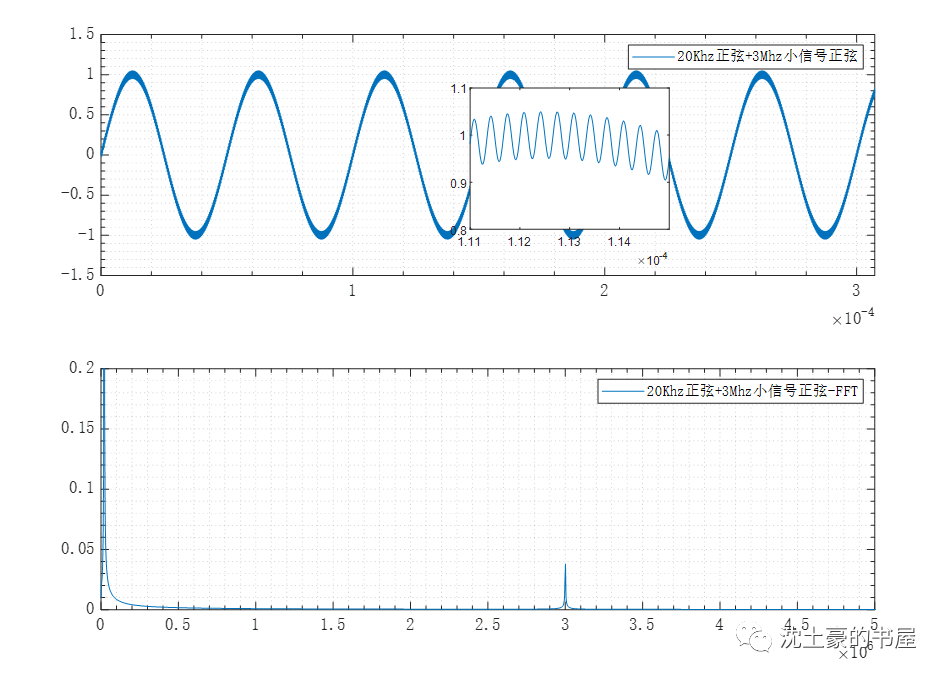
C.低頻信號混入高頻噪聲小信號時頻表現

如圖所示為3Mhz正弦混入20Khz正弦小信號噪聲，這種情況下噪聲會以小幅度，高周期性的疊加在低頻的正弦上，表現為原本干凈的20Khz正弦在時域上“變粗”，打開粗的地方，我們可以看到曲線上混入了高頻的正弦起起伏伏，如下圖小圖中所示（小圖中所示的正弦頻率即3Mhz）。

直觀的講：低頻混入高頻小信號，在時域上即波形變粗。

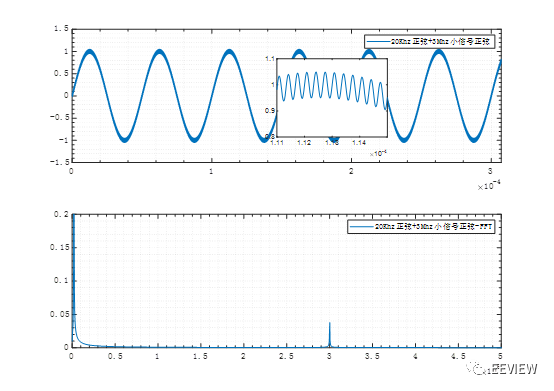
圖 3?1 3Mhz正弦混入20Khz正弦小信號噪聲

f3=0.02*1e6;f4=3*1e6;

y2=1sin(2pif3t)+0.05sin(2pif4t);

通過FFT可以看到高頻小信號噪聲對應的幅值是比較小的，正是這種小幅度，才會引起波形變粗。

D.高頻混低頻、低頻混高頻噪聲小信號對比

通常噪聲都是小幅度的，就有了以下的結論：

• 高頻混入低頻小信號噪聲：擴大時基看包絡
• 低頻混入高頻小信號噪聲：縮小時基看局部

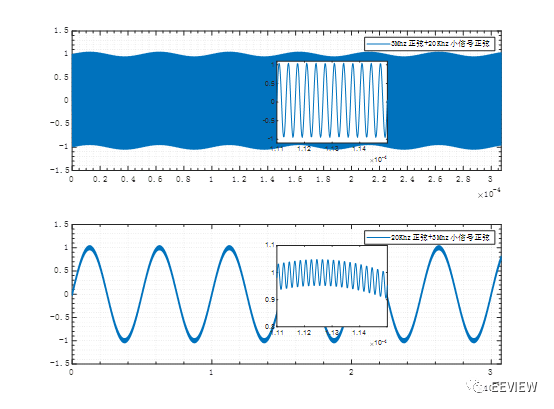
圖 4?1對比效果圖