什么是遞歸?
要說到遞歸如果不說棧的話,我覺得有點不合適,遞歸特點就是不斷的調用同一個函數,如果這個函數沒有一個遞歸界限,那么就是死循環了,所以討論遞歸,就必須要討論遞歸的界限,就是限定這個遞歸調用多少次。
我們看一個例子
#include "stdio.h"
int digui(unsigned long count )
{
if(count > 0){
count --;
printf("%d \\n",count);
digui(count);
}
return 1;
}
int main()
{
digui(10);
return (100);
}
這個遞歸函數的限定判讀是
if(count > 0){
所以他的調用順序可以用這個圖示來說明
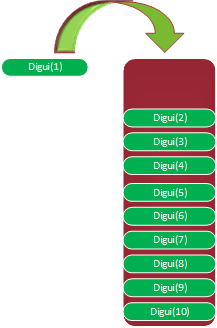
這個過程叫做遞去,也就是壓棧的過程,既然有壓棧的過程,那么就有出棧的過程,出棧的過程就是
if(count > 0){
判斷不成功后,就會出棧了。如下圖所示
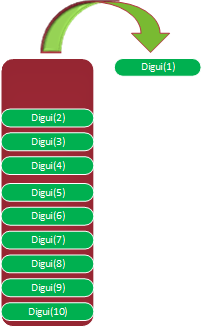
一共能執行多少次遞歸?
我們上面說到了,既然遞歸使用了棧,那么系統的棧的大小肯定是有極限的,不可能系統給你分配無極限的棧的大小,我看一些文章說棧大小是64K。
還是上面那個例子,我把傳入數據設置為很大執行看看。
#include "stdio.h"
int tigui(unsigned long count )
{
if(count > 0){
count --;
printf("%d \\n",count);
tigui(count);
}
return 1;
}
int main()
{
tigui(900000);
return (100);
}
執行結果
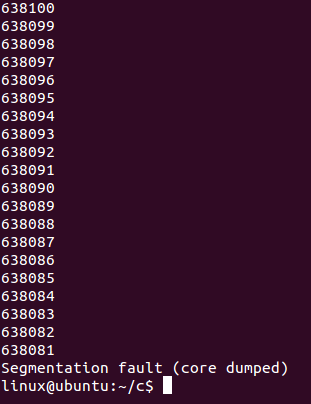
所以說遞歸次數肯定是有限定的了。
遞歸求階乘
使用遞歸求階乘是很經典的方法,我們看一下代碼。
#include< stdio.h >
int fact(unsigned long n); //聲明階乘fact函數
int main(){
unsigned long x;
scanf("%d",&x);
x = fact(x);//調用函數返回int值
printf("%ld\\n",x);
return (0);
}
int fact(unsigned long n){//定義階乘函數
if(n==1) return 1;//輸入的參數是1,直接返回1
else return n*fact(n-1);//遞歸算法
}
執行結果
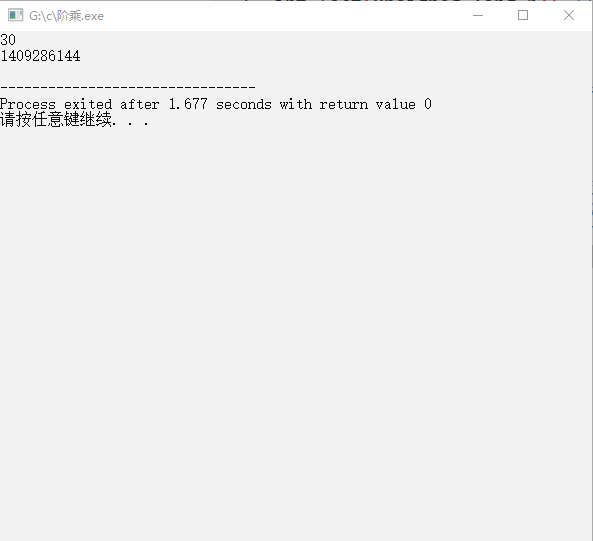
單看代碼我覺得還是有點拗口 我們看個圖片來看他的調用,假設我們要求的是 5 的階乘

遞歸和漢諾塔
漢諾塔: 漢諾塔(又稱河內塔)問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定,在小圓盤上不能放大圓盤,在三根柱子之間一次只能移動一個圓盤。
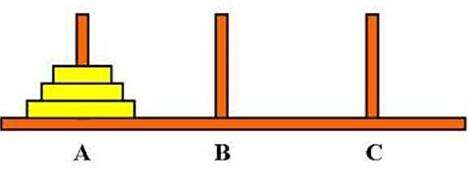
如果是這樣的漢諾塔,我覺得應該每個人都覺得很簡單吧,只需要三步就可以完成移動。
- 1、把小圓盤放到第三根柱子上
- 2、把中圓盤放到第二根柱子上
- 3、把小圓盤放到第二根柱子上
- 4、把大圓盤放到第三根柱子上
- 5、把小圓盤放到第一根柱子上
- 6、把中圓盤放到第三根柱子上
- 7、把小圓盤放到第三根柱子上
如圖所示
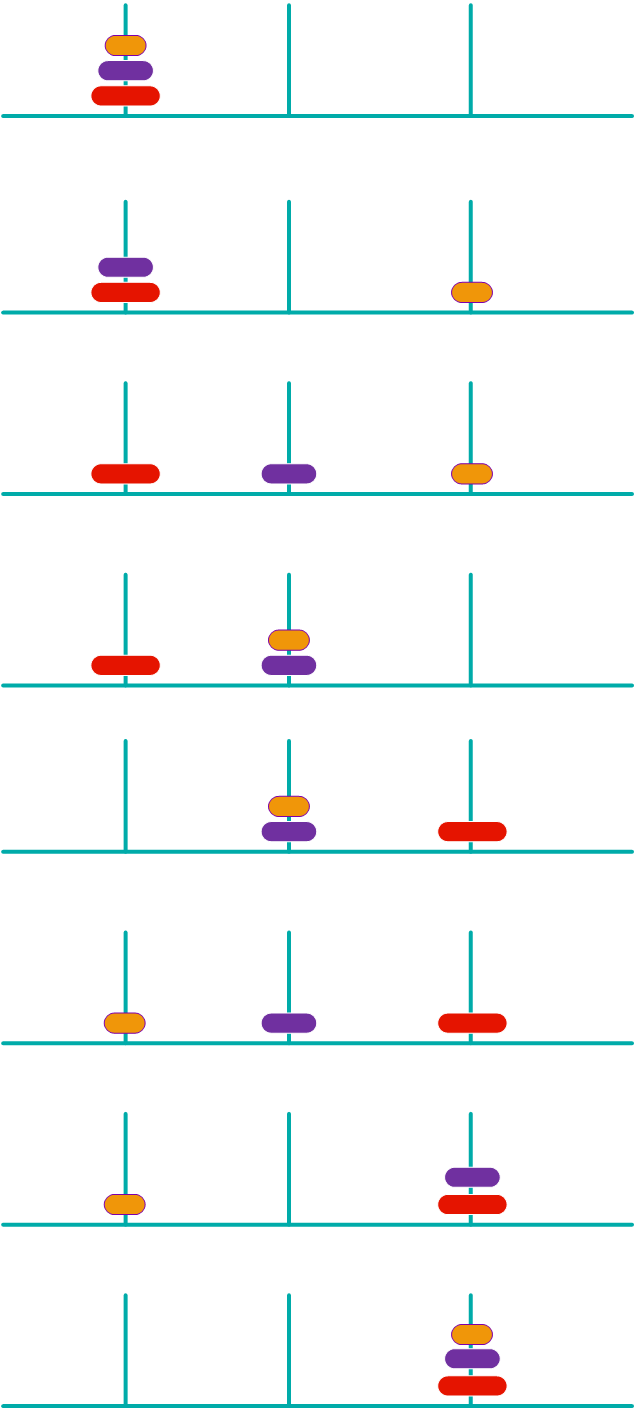
剖析我們上面是細分的方法,移動的核心思想分為三步。
- 1、把第一個柱子上的n-1圓盤移動到第二個柱子上。
- 2、把第一個柱子的第n個圓盤移動到第三個柱子上。
- 3、把第二個柱子的n-1個圓盤移動到第三個柱子。
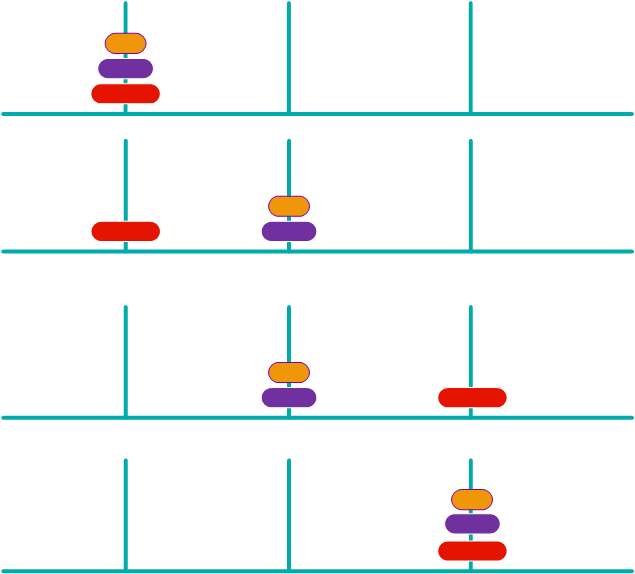
所以遞歸就出現了
- 1、把第一個柱子上的n-1圓盤移動到第二個柱子上「 遞歸實現 」。
- 2、把第一個柱子的第n個圓盤移動到第三個柱子上。
- 3、把第二個柱子的n-1個圓盤移動到第三個柱子「 遞歸實現 」。
C語言代碼實現
#include < stdio.h >
#include < windows.h >
void Hanoi(int n, char a,char b,char c);
void Move(int n, char a, char b);
int count;
int main()
{
int n=8;
printf("漢諾塔的層數:\\n");
scanf(" %d",&n);
Hanoi(n, 'A', 'B', 'C');
printf("Exiting main...\\n");
return 0;
}
void Hanoi(int n, char a, char b, char c)
{
if (n == 1)
{
Move(n, a, c);
}
else
{
Hanoi(n - 1, a, c, b);/*把 n-1 從 a 柱子放到 b 柱子上面*/
Move(n, a, c); /*把 n 從 a 移動到 c 上*/
Hanoi(n - 1, b, a, c);/*把n - 1 通過 a 的輔助作用 從 b 移動到 c 上*/
}
}
void Move(int n, char a, char b)
{
count++;
printf("第%d次移動 Move %d: 從 %c 位置 移動到 %c !\\n",count,n,a,b);
}
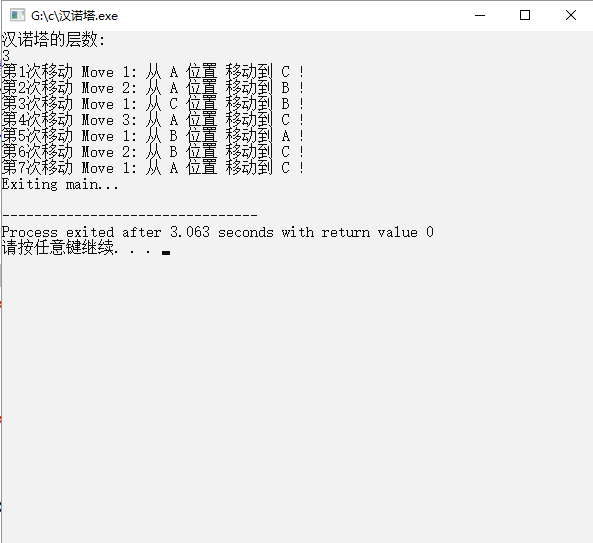
輸出如圖所示
加強版修改
加強了下軟件寫法,好好看代碼,寫的有點太快,沒細想,后面再完善。
#include < stdio.h >
/*柔性數組*/
typedef struct _soft_array{
int len;
int array[];
}soft_array;
/*漢諾塔結構體*/
typedef struct _hannuo{
soft_array *p_data;
char name;
}hannuo;
hannuo * han_a = NULL;
hannuo * han_b = NULL;
hannuo * han_c = NULL;
void hannoiii(int n,hannuo * a,hannuo * b,hannuo * c);
void moveiii (int n,hannuo * a,hannuo * c);
int total;
void printf_han_data(hannuo * han)
{
int i = 0;
printf("%c: ",han- >name);
/*輸出漢諾塔的數據*/
for(i = 0;i< han- >p_data- >len;i++)
{
printf("%d-",han- >p_data- >array[i]);
}
printf("\\n");
}
int main()
{
int i = 0;
int n = 0;
scanf(" %d",&n);
total = n;
/*定義三個漢諾塔節點*/
han_a = (hannuo *)malloc(sizeof(hannuo));
han_a- >name = 'A';
han_a- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
han_a- >p_data- >len = n;
/*數據原來在第一根柱子上*/
for(i = 0;i< n;i++)
{
han_a- >p_data- >array[i] = i+1;
}
printf_han_data(han_a);
/*初始化第二根柱子*/
han_b = (hannuo *)malloc(sizeof(hannuo));
han_b- >name = 'B';
han_b- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
memset(han_b- >p_data,0,sizeof(soft_array)+sizeof(int)*n);
han_b- >p_data- >len = n;
printf_han_data(han_b);
/*初始化第三根柱子*/
han_c = (hannuo *)malloc(sizeof(hannuo));
han_c- >name = 'C';
han_c- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
memset(han_c- >p_data,0,sizeof(soft_array)+sizeof(int)*n);
han_c- >p_data- >len = n;
printf_han_data(han_c);
printf("------------------------\\n");
hannoiii(n,han_a,han_b,han_c);
printf("\\n");
return 0;
}
void hannoiii(int n,hannuo * a,hannuo * b,hannuo * c)
{
if(n == 1)
{
a- >p_data- >array[




 C語言,你真的懂遞歸了嗎?
C語言,你真的懂遞歸了嗎?