本文很好地介紹了模擬濾波器。它涵蓋了基本的一階和二階濾波器類型以及無源和有源濾波器的優(yōu)缺點。本文使用多個運算放大器實現(xiàn)示例推導(dǎo)并分析了基本的雙二階實現(xiàn)方案。

濾波器設(shè)計的世界通常被認(rèn)為是黑魔法，因為有無數(shù)的配置、獨特的術(shù)語和復(fù)雜的方程式。本應(yīng)用筆記將介紹不同的濾波器類型，闡明術(shù)語，并為選擇提供基礎(chǔ)，使濾波器的設(shè)計更加科學(xué)，少了一點魔力。我們將主要關(guān)注低通濾波器，盡管帶通和高通濾波器都可以使用相同的方法進(jìn)行分析和設(shè)計。

出現(xiàn)的第一個問題是：我是否可以使用簡單的無源濾波器（即僅使用電阻器、電容器和電感器等無源元件，而不使用運算放大器），還是最好使用有源濾波器。無源濾波器的優(yōu)點是設(shè)計和實現(xiàn)非常簡單。它還提供一個簡單的單極或兩極濾波器，其電響應(yīng)可以輕松計算。對于單極點低通濾波器，fc = 1/（2 × π × RC），濾波器滾降為每倍頻程6dB或20dB/十倍頻程。但是，此過濾器確實有一些明顯的缺點：

它對元件值公差非常敏感。

對于低頻，R和C的值可能相當(dāng)大，導(dǎo)致物理上較大的組件。

一階或二階濾波器可能無法提供足夠的滾降

如果電路中需要增益，則不能將其添加到濾波器本身。

濾波器可能具有高輸出阻抗。由于電阻值通常很大，為了保持電容的合理值，下一級器件可以看到顯著的源阻抗。可以在輸出端增加一個運算放大器，但是，除了降低輸出阻抗之外，它還可用于改善濾波器的性能，為什么要在這里添加運算放大器呢？

如果無源濾波器不能滿足您的需求，您可以選擇有源濾波器。通過增加運算放大器，我們可以輕松實現(xiàn)二階濾波器。二階濾波器通常是高階濾波器的構(gòu)建塊，因為它們可以很容易地級聯(lián)以獲得高階濾波器。濾波器的一般形式可以寫成等式形式，如下所示：

H（s） = K （s + z1）（S + z2）/[（s + p1）（s + p2）]

這個方程稱為雙二次方程，簡稱為雙二元方程。分子中的zn項表示零，分母中的pn項表示極點。查看等式，首先清楚的是可以以這種形式編寫的過濾器是雙二階。這意味著Sallen-Key濾波器，狀態(tài)變量變量濾波器，多反饋濾波器和其他類型的都是雙二階的。還有一個“雙四”拓?fù)鋪韼椭M(jìn)一步混淆事物。因此，真正的濾波器名稱是雙二階 Sallen-Key、雙二階狀態(tài)變量和二階（稍后會解釋）。

以低通濾波器為例，低通濾波器可以用一般方程形式編寫為：

H（s） = K/（as2 + bs + 1），其中 a = R1R2C1C2 和 b = R1C1 + R2C1

這可以通過使 R1 = R2 和 C1 = C2 來簡化，從而得到：

H（s） = K/（R2C2s2 + 2RCs + 1）

低通二階Sallen-Key濾波器的框圖如圖2所示。該濾波器也稱為正反饋濾波器，因為輸出反饋到運算放大器的正端。這種拓?fù)浜苁軞g迎，因為它只需要一個運算放大器，因此相對便宜。

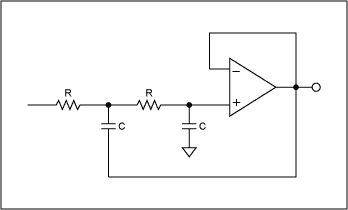
圖1.等分量值，薩倫基低通濾波器。

但是，此拓?fù)浯嬖谝恍┤秉c。首先，它可以獲得的最大Q值非常有限，因此不建議用于需要高Q值的應(yīng)用。濾波器的Q值是“質(zhì)量”因子，它基本上給出了存儲的能量與共振時耗散的能量之比。高 Q 值濾波器可實現(xiàn)非常尖銳的濾波器滾降。就s平面而言，高Q值濾波器的極點更靠近jw軸。請記住，只要極點位于jw軸的左側(cè)，設(shè)備理論上是穩(wěn)定的。隨著極點越來越接近jw軸，穩(wěn)定性降低。現(xiàn)在回到Q因子。在選擇或設(shè)計帶通濾波器時，通常使用Q因數(shù)。Q的倒數(shù)是阻尼因數(shù)，在低通和高通應(yīng)用中更為相關(guān)。對于單個運算放大器Sallen-Key濾波器，Q值通常約為5左右。

另一個缺點是，與放大器所需的最小開環(huán)增益（3Q2）相比，該電路的增益相對較低（-90Q）。這意味著放大器的GBW積必須明顯高于濾波器的最大截止頻率，從而使放大器的性能高于預(yù)期，以確保其不會限制對濾波器響應(yīng)產(chǎn)生不利影響。

為了獲得稍高的Q值，讓我們轉(zhuǎn)到圖2所示的多反饋無限增益架構(gòu)。這種拓?fù)渫瑯有枰粋€放大器，并提供25范圍內(nèi)的Q值。使用這種拓?fù)洌鲆妫?2Q2）與放大器GBW積（諧振時為20Q2）相比仍然相對較低，但不如Sallen-Key方法低。

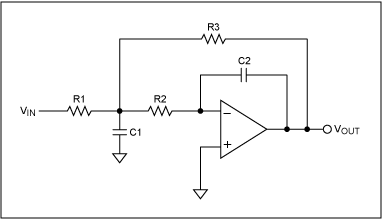
圖2.無限脈沖、多反饋低通濾波器。

但請注意，這種拓?fù)浣Y(jié)構(gòu)反轉(zhuǎn)了信號，并注意到增益和Q值與Sallen鍵密不可分。Sallen Key和多重反饋架構(gòu)對外部組件變化也相當(dāng)敏感。為了轉(zhuǎn)向更可靠的濾波器，我們現(xiàn)在考慮3和4運算放大器狀態(tài)可變和雙二階架構(gòu)。

狀態(tài)變量雙二階

圖3顯示了3個放大器狀態(tài)變量Biquad的基本架構(gòu)。它包括一個求和節(jié)點，后跟兩個積分器。這種架構(gòu)非常通用，因為它提供了高通、帶通和低通輸出，但它也允許獨立控制fc和Q。

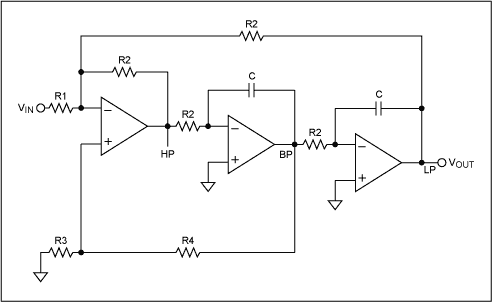
圖3.三個放大器狀態(tài)可變雙二階。

通過增加第 4 個放大器，實現(xiàn)了 Q 和增益的獨立控制（圖 4）。狀態(tài)變量是高Q值電路的理想選擇。通過適當(dāng)?shù)臑V波器設(shè)計，可以輕松達(dá)到 500 或更高的 Q。與單運放架構(gòu)不同，開環(huán)增益（3Q）只需略高于濾波器的輸出增益（Q），低通增益為Q，這降低了對運算放大器GBW的要求（請注意，對于Sallen-Key，運算環(huán)路增益必須至少為90Q2，Q為500時為22.5MHz。

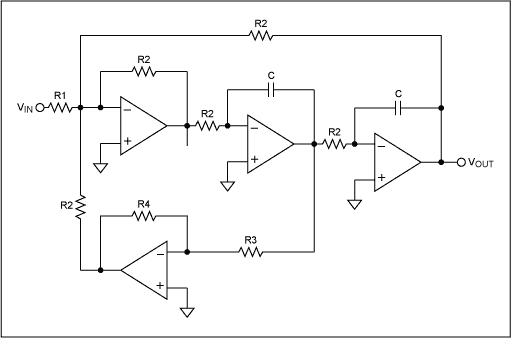
圖4.雙二階狀態(tài)變量濾波器，具有獨立控制 q/阻尼。

在到目前為止討論的拓?fù)渲校鹗甲兞繉M件變化最不敏感。它還具有另一個獨特的屬性：隨著頻率fc的變化，Q和百分比帶寬保持不變。也就是說，當(dāng)您在頻域中移動fc時，Q值保持不變，但濾波器的帶寬隨著fc的增加而減小，隨著fc的減小而增加。帶寬百分比定義為 100% × （（F在， gL）/（√ F在×FL） 其中 F在是上 3dB 帶寬點，F(xiàn)L是較低的 3dB 帶寬點和 √F在×FL是 FC。

狀態(tài)變量設(shè)計的主要缺點是使用3或4個放大器。對于功耗敏感型應(yīng)用尤其如此。由于可用的過濾器軟件和過濾器設(shè)計食譜過多，設(shè)計本身相當(dāng)簡單。但是，當(dāng)使用高Q值時，必須非常小心布局和組件選擇。這是因為高Q值電路容易表現(xiàn)出不穩(wěn)定，并伴有輕微的元件不匹配。由于這種不穩(wěn)定性，它們也更有可能振蕩。

雙二階濾波器

最后，我們看一下雙二階濾波器（圖5）。它與上面顯示的狀態(tài)變量雙二階非常相似。然而，它包括一個積分器，然后是一個逆變器，然后是另一個積分器。請注意，這種細(xì)微的變化提供了一個行為與狀態(tài)變量濾波器不同的電路。

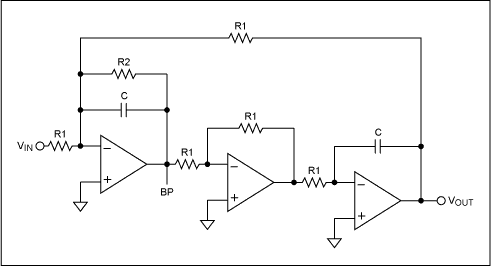
圖5.雙二階濾波器。

最大的區(qū)別在于，對于雙二階，當(dāng)fc發(fā)生變化時，帶寬保持不變，但Q值會發(fā)生變化。因此，如果在頻域中更改fc，隨著fc的增加，Q值增加，隨著fc的減小，Q值也會減小。除了這種差異之外，雙二階運算的行為類似于狀態(tài)變量。它允許非常高的Q值，可以配置為3或4放大器配置，并且對外部元件變化也不太敏感。3和4放大器電路消耗更多功率，通常需要更多設(shè)計時間，特別是當(dāng)多個級級聯(lián)以獲得更陡峭的濾波器滾降響應(yīng)時。此外，由于單個放大器比四通道放大器便宜，因此成本更高。從性能的角度來看，它要好得多，這是必須做出的權(quán)衡。

您可以使用上述操作放大器技術(shù)設(shè)計濾波器。Maxim擁有多種高速、高精度運算放大器，可用于濾波器設(shè)計。如果您不想自己設(shè)計，可以選擇MAX274/MAX275集成濾波器。這些單芯片解決方案分別配置為由二階構(gòu)建模塊組成的 8 階（8 極）和 4 階（4 極）濾波器。

這些連續(xù)時間濾波器采用雙二階架構(gòu)，提供低通和帶通輸出。

審核編輯：郭婷