1.概述
在進(jìn)行代碼分析之前,了解Mahony濾波器的原理和公式推導(dǎo)是必要的。Mahony濾波器是一種基于四元數(shù)的姿態(tài)估計(jì)濾波器,其主要思想是通過(guò)加速度計(jì)和陀螺儀的測(cè)量值來(lái)估計(jì)姿態(tài),并通過(guò)四元數(shù)來(lái)表示姿態(tài)。其公式推導(dǎo)涉及到四元數(shù)的運(yùn)算和旋轉(zhuǎn)矩陣的推導(dǎo),需要具備一定的數(shù)學(xué)基礎(chǔ)和姿態(tài)估計(jì)相關(guān)的知識(shí)。
四元數(shù)是一種數(shù)學(xué)工具,它可以用來(lái)表示三維空間的旋轉(zhuǎn)信息。在秦永元的《慣性導(dǎo)航》這本書第9.2章節(jié)中,介紹了姿態(tài)更新計(jì)算的四元數(shù)算法,其中詳細(xì)講解了四元數(shù)的概念、四元數(shù)與姿態(tài)陣之間的關(guān)系以及四元數(shù)微分方程。閱讀完9.2章節(jié)的推導(dǎo)后,我們可以更深入地理解四元數(shù)的應(yīng)用和原理。
之前我也寫過(guò)一篇 《MEMS_慣性傳感器09 - Mahony姿態(tài)解算算法詳解》,但是還是建議閱讀秦永元的《慣性導(dǎo)航》,這樣更容易理解。
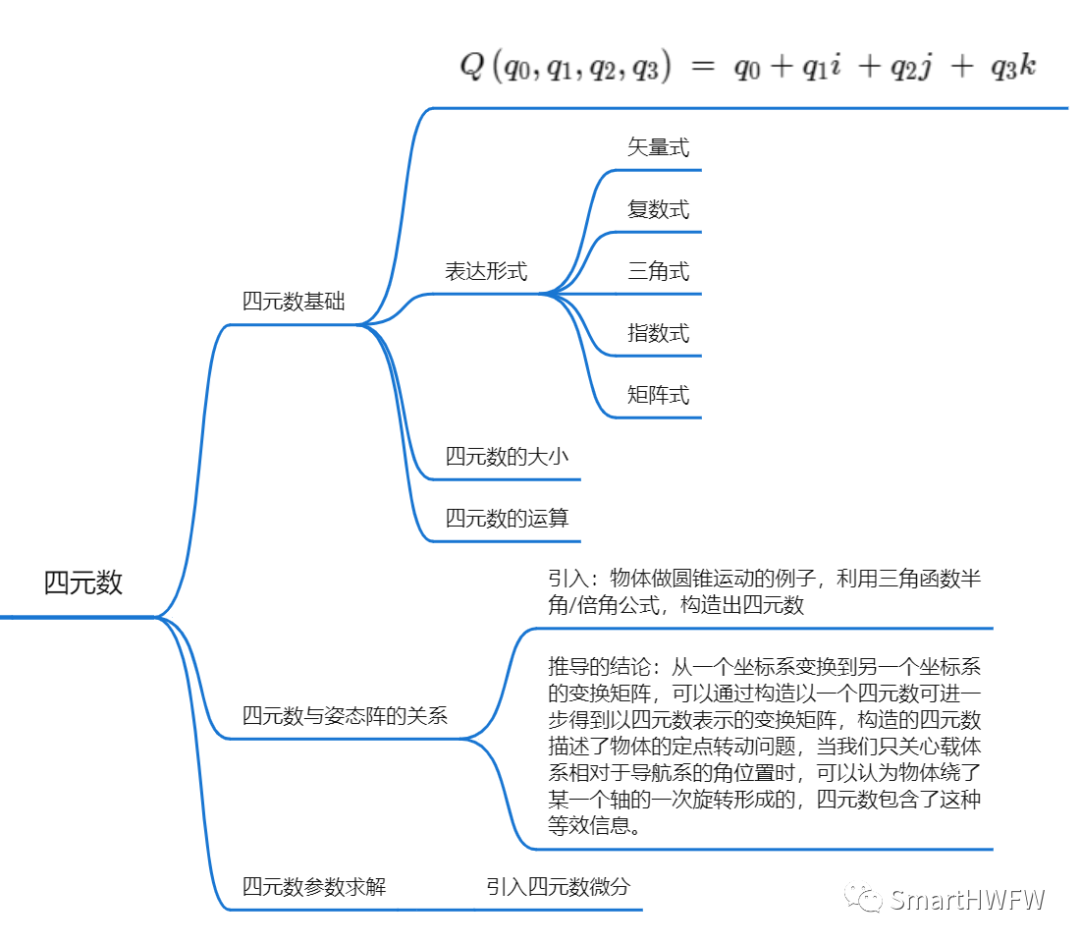
物體的姿態(tài)變化可以等效為繞某個(gè)軸的一次旋轉(zhuǎn)。我們不需要關(guān)注物體變化的中間過(guò)程,只需要找到一種變換關(guān)系,就能夠求出物體從導(dǎo)航坐標(biāo)系到載體坐標(biāo)系或從載體坐標(biāo)系到導(dǎo)航坐標(biāo)系的坐標(biāo)。因此,我們需要推導(dǎo)出這種變化關(guān)系。
利用四元數(shù)與姿態(tài)陣的關(guān)系,可以推導(dǎo)得到如下結(jié)論:
(1) 四元數(shù) Q (表達(dá)式如下) 描述了物體的定點(diǎn)轉(zhuǎn)動(dòng),即,當(dāng)之關(guān)心 b 系(載體系)相對(duì)于 R 系(導(dǎo)航系)的角位置時(shí),可認(rèn)為 b 系是由 R系經(jīng)過(guò)無(wú)中間過(guò)程的一次性等效旋轉(zhuǎn)形成的。
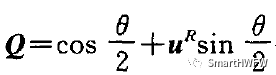
Q包含了這種等效旋轉(zhuǎn)的全部信息;u^R 為旋轉(zhuǎn)瞬間和旋轉(zhuǎn)方向 θ為旋轉(zhuǎn)過(guò)的角度
(2) 四元數(shù)可以確定出 b 系至 R 系的坐標(biāo)變換矩陣
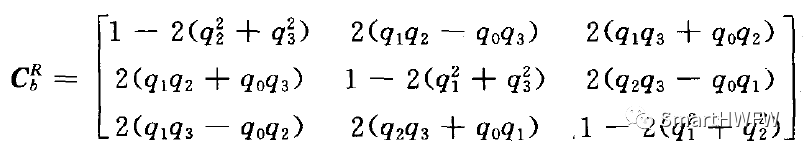
根據(jù)上述推導(dǎo),已經(jīng)得到了姿態(tài)變換矩陣和四元數(shù)表示法中的姿態(tài)角。然而,目前四元數(shù)的具體數(shù)值未知。為了得到真正的姿態(tài)角,需要找到確定四元數(shù)數(shù)值的方法。
通過(guò)已知的陀螺儀和加速度計(jì)獲得的角速度和加速度,我們可以利用四元數(shù)微分來(lái)求解四元數(shù)的具體數(shù)值。四元數(shù)微分是指將四元數(shù)看作一個(gè)向量,然后對(duì)其進(jìn)行微分,得到一個(gè)表示四元數(shù)變化率的向量。通過(guò)對(duì)四元數(shù)微分的計(jì)算,可以得到四元數(shù)的具體數(shù)值。
通過(guò)解微分方程,可以計(jì)算四元數(shù)的參數(shù)
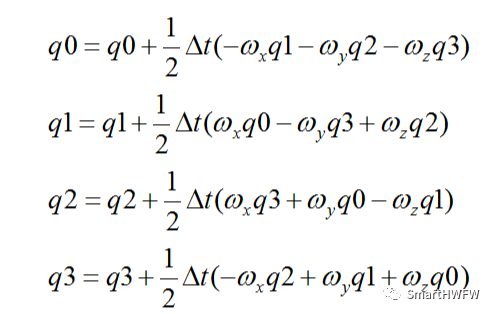
以上公式的推導(dǎo)過(guò)程已在書中詳細(xì)說(shuō)明,故本文不再贅述。針對(duì)誤差消除,本文采用了Mahony濾波算法,該算法是本文的核心內(nèi)容。
2.陀螺儀誤差的消除
角度測(cè)量中存在偏差,由于角速度是積分得到的,陀螺儀獲得的角速度信息存在小的偏差,積分后誤差會(huì)不斷累積,導(dǎo)致角度測(cè)量結(jié)果偏差較大。雖然加速度計(jì)獲得的角度信息不會(huì)出現(xiàn)偏差,但其受噪聲影響較大,短時(shí)間內(nèi)可靠性不高。因此,我們可以利用加速度計(jì)獲得的角度信息去矯正陀螺儀獲得的姿態(tài)信息,從而消除算出來(lái)的角度誤差。
核心思想是利用加速度計(jì)獲取信息來(lái)補(bǔ)償陀螺儀的角速度信息。具體實(shí)現(xiàn)步驟如下:
1.獲取加速度的值,并對(duì)其歸一化 (歸一化是為了確保姿態(tài)變化矩陣中的四元數(shù)是規(guī)范四元數(shù),并且利用陀螺儀更新的四元數(shù)也需要?dú)w一化。以確保與其他數(shù)據(jù)對(duì)應(yīng))
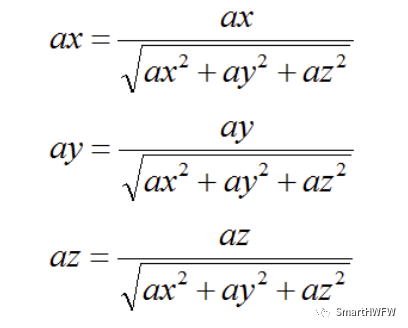
//Normaliseaccelerometermeasurement recipNorm = invSqrt(ax * ax + ay * ay + az * az); ax *= recipNorm; ay *= recipNorm; az *= recipNorm;
2.獲取陀螺儀算出的姿態(tài)矩陣中的重力分量, 重力分量記為Vx、Vy、Vz
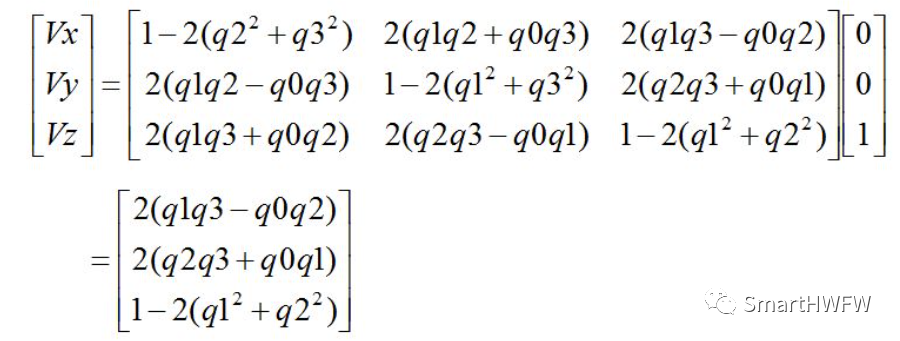
// Estimated direction of gravity and vector perpendicular to magnetic flux halfvx = q1 * q3 - q0 * q2; halfvy = q0 * q1 + q2 * q3; halfvz = q0 * q0 - 0.5f + q3 * q3;
3.獲取姿態(tài)誤差,(將第一步中 獲取的重力向量歸一化后的值與提取的姿態(tài)矩陣的重力向量叉乘)
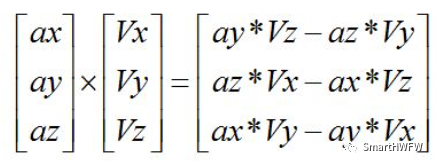
// Error is sum of cross product between estimated and measured direction of gravity halfex = (ay * halfvz - az * halfvy); halfey = (az * halfvx - ax * halfvz); halfez = (ax * halfvy - ay * halfvx);
4.消除誤差, (通過(guò)對(duì)重力分量叉乘后的誤差進(jìn)行積分,可以得到角速度值。ki為積分系數(shù),dt為積分周期)
integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki integralFBy += twoKi * halfey * (1.0f / sampleFreq); integralFBz += twoKi * halfez * (1.0f / sampleFreq); gx += integralFBx; // apply integral feedback gy += integralFBy; gz += integralFBz;
5.互補(bǔ)濾波(在PID控制器中加入誤差值,并將其與陀螺儀測(cè)得的角速度相加,得到修正的角速度值。使用修正的角速度值來(lái)更新四元素,以獲得更準(zhǔn)確的姿態(tài)角信息)
// Apply proportional feedback gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez; //Integrate rate of change of quaternion gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors gy *= (0.5f * (1.0f / sampleFreq)); gz *= (0.5f * (1.0f / sampleFreq));
6.求解微分方程
qa = q0; qb = q1; qc = q2; q0 += (-qb * gx - qc * gy - q3 * gz); q1 += (qa * gx + qc * gz - q3 * gy); q2 += (qa * gy - qb * gz + q3 * gx); q3 += (qa * gz + qb * gy - qc * gx);
7.四元數(shù)歸一化
// Normalise quaternion recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm;
8.四元數(shù)求解歐拉角 (在求解角度時(shí)要清楚的知道導(dǎo)航坐標(biāo)系是:東北天; 北東地)
roll = asinf(2 * q0 * q2 - 2 * q1 * q3) * (180 / M_PI); // 繞X軸旋轉(zhuǎn) pitch = atan2f(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * (180 / M_PI); // 繞Y軸旋轉(zhuǎn) yaw = atan2f(2 * q1 * q2 + 2 * q0 * q3, -2 * q2 * q2 - 2 * q3 * q3 + 1) * (180 / M_PI); // 繞Z軸旋轉(zhuǎn)
3.算法效果演示
不足:
1)當(dāng)X軸角度大于90度時(shí),Y軸角度發(fā)生了漂移
2)在從旋轉(zhuǎn)到靜止的過(guò)程之后,Z軸角度沒(méi)有趨近于0度。
責(zé)任編輯:彭菁
-
濾波器
+關(guān)注
關(guān)注
162文章
8101瀏覽量
181324 -
導(dǎo)航
+關(guān)注
關(guān)注
7文章
549瀏覽量
43054 -
慣性傳感器
+關(guān)注
關(guān)注
2文章
177瀏覽量
28310
原文標(biāo)題:MEMS_慣性傳感器14 - Mahony 濾波算法的代碼分析
文章出處:【微信號(hào):SmartHWFW,微信公眾號(hào):SmartHWFW】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
求Sigmadsp的高階濾波器計(jì)算公式
抗EMI濾波器設(shè)計(jì)與應(yīng)用原理
LC低通濾波器的截止頻率是怎么推導(dǎo)出來(lái)的?公式是什么?

帶通濾波器到低通濾波器的轉(zhuǎn)換公式推導(dǎo)資料合集
一階數(shù)字低通濾波器原理及公式推導(dǎo)
如何理解卡爾曼濾波器?卡爾曼濾波器狀態(tài)方程及測(cè)量方程
低通濾波器截止頻率計(jì)算公式_作用和用途
模擬無(wú)源濾波器設(shè)計(jì)(九)-Gaussian濾波器設(shè)計(jì)詳解
在連續(xù)時(shí)間域中比較Papoulis濾波器和Chebyshev濾波器

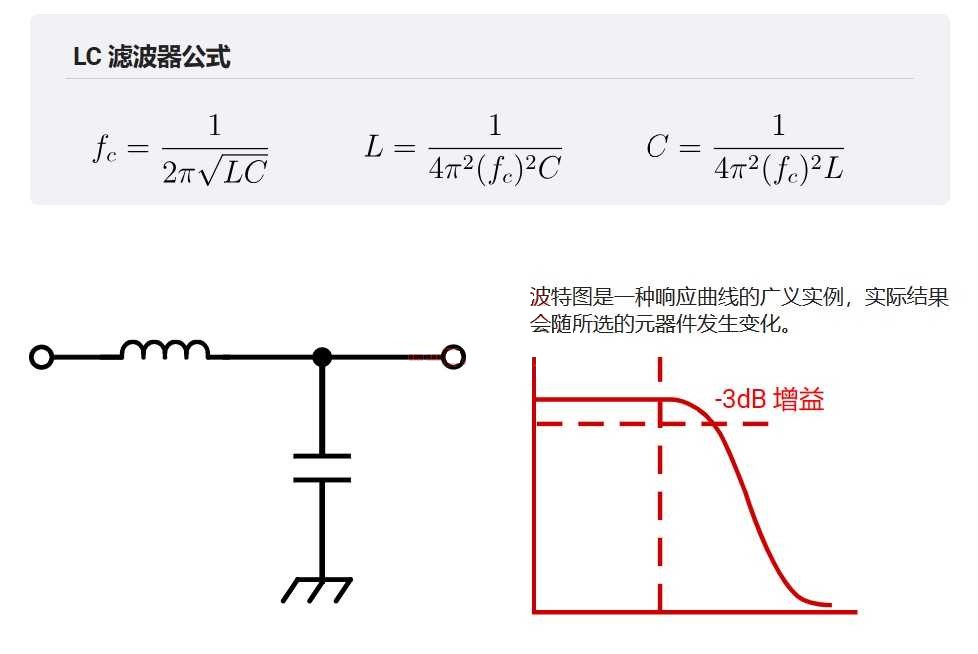
LC 濾波器公式 - LC filter





 Mahony濾波器的原理和公式推導(dǎo)
Mahony濾波器的原理和公式推導(dǎo)










評(píng)論