開環(huán)/閉環(huán)函數(shù)波特圖的關(guān)系
為簡(jiǎn)化問題,以單位負(fù)反饋系統(tǒng)為例說明。環(huán)路,loop gain,也就是我們常說的"開環(huán)傳遞函數(shù)"就是G,整體的閉環(huán)傳遞函數(shù)就是T。
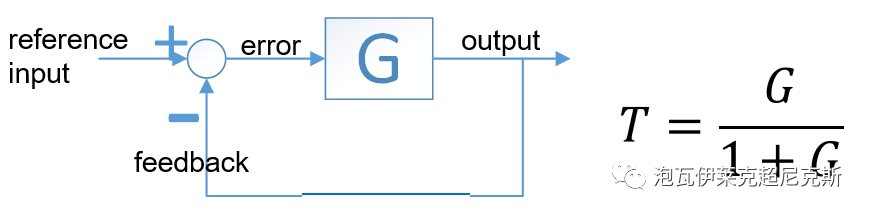
在工程習(xí)慣中,G會(huì)被直接用來做loop gain環(huán)路分析,觀察其穿越頻率ωc,增益相位裕度GM,PM;而T在基于頻域設(shè)計(jì)的方法論中,很少被直接關(guān)注,但T才是最直接反應(yīng)閉環(huán)后,輸入輸出對(duì)應(yīng)頻率特性的。
通過開環(huán)函數(shù)G的波特圖直接設(shè)計(jì)系統(tǒng)性能,其實(shí)是以G間接預(yù)估閉環(huán)函數(shù)T的頻率特性,從而完成對(duì)T的設(shè)計(jì)。
(此處概念混淆,以及不清楚為何引入開環(huán)傳遞函數(shù)判斷閉環(huán)系統(tǒng)穩(wěn)定性的讀者,請(qǐng)自行復(fù)習(xí)“自動(dòng)控制原理”課本中關(guān)于穩(wěn)定性和頻率特性的章節(jié))
以典型一階和二階系統(tǒng)展示G和T的關(guān)系:


-
結(jié)論:
1. G的增益超過0dB(增益大于1)的低頻段,由于T=G/(1+G) (注意是復(fù)數(shù)計(jì)算) ,T的增益會(huì)接近1(0dB);越低頻增益越高,T的增益約接近1(0dB),越能對(duì)低頻信號(hào)實(shí)現(xiàn)無誤差地跟蹤。
2. 0dB以下的高頻段,G的增益越低,那么T對(duì)應(yīng)的增益也會(huì)越低。
3. G的相位體現(xiàn)在 T=G/(1+G) 的復(fù)數(shù)計(jì)算中,相位偏移較多時(shí),有可能在T的該頻段造成諧振峰.
穿越頻率和帶寬的關(guān)系
回顧定義如下:
- 開環(huán)截止頻率ωc也稱為穿越頻率(crossover frequency),是開環(huán)G幅頻特性曲線穿越0dB(增益=1)時(shí),對(duì)應(yīng)的頻率;
- 閉環(huán)截止頻率ωb也稱為帶寬頻率(bandwidth),是閉環(huán)T幅頻特性下降到-3dB(增益=1/根號(hào)2)時(shí),對(duì)應(yīng)的頻率。
那么兩者的關(guān)系,推導(dǎo)如下:(注意在帶寬ωb附近,一般的控制系統(tǒng)都有積分環(huán)節(jié)存在(如PI),G的相角在-90°-180°,故G中α(ωb)<0成立)


- 結(jié)論:
穩(wěn)定的負(fù)反饋系統(tǒng),開環(huán)系統(tǒng)的穿越頻率和閉環(huán)系統(tǒng)的帶寬很接近,存在ωb>ωc且有同向性。工程上近似時(shí),時(shí)常把兩者直接混用。
帶寬和動(dòng)態(tài): 窺一斑,能否見全豹?
由閉環(huán)系統(tǒng)T的帶寬推測(cè)動(dòng)態(tài)性能最為直觀:帶寬越高,越多頻率分量的信號(hào)放大增益在-3dB以上,可以被有效跟蹤,因此動(dòng)態(tài)性能越好。但是,尤其注意以下:
- 結(jié)論:
穿越頻率/帶寬描述的僅僅是頻域上一個(gè)點(diǎn)的信息,是“窺一斑而見全豹”的做法, 僅可當(dāng)作指導(dǎo)性的規(guī)律揭示, 并不能直接用于比較兩個(gè)系統(tǒng)的動(dòng)態(tài)!
動(dòng)態(tài)響應(yīng)由全頻率段的幅頻/相頻特性共同決定。

給出如下例子,讓我們加深對(duì)帶寬和動(dòng)態(tài)關(guān)系的理解。
- 例子1: 帶寬小的 系統(tǒng)1 ,動(dòng)態(tài)反而快于帶寬大的 系統(tǒng)2 !!!
究其原因,正是因?yàn)榍≡趲捀浇念l段,系統(tǒng)2的增益高于系統(tǒng)1,但在其他頻段,系統(tǒng)1的增益均高于系統(tǒng)2。

- 例子2:相同的帶寬和低頻增益,導(dǎo)致從0到1的建立時(shí)間近似相同,但由于高頻增益不同,動(dòng)態(tài)響應(yīng)的速度完全不同(期間的凹凸特性):

- 例子3:相同的帶寬和高頻增益,但由于低頻增益諧振峰的不同,動(dòng)態(tài)響應(yīng)的速度完全不同(包括超調(diào)):

那么,“帶寬越大,動(dòng)態(tài)越快” 這個(gè)結(jié)論是怎么來的?
- 例子4:相同的系統(tǒng)結(jié)構(gòu)(頻率特性的全局分布一致),帶寬越高,動(dòng)態(tài)越快:

可以看到,當(dāng)且僅當(dāng)你要做比較的若干個(gè)系統(tǒng),其有相同(或相近)的系統(tǒng)結(jié)構(gòu),也即頻率特性的全局分布一致(或類似)時(shí),才有老生常談的這句經(jīng)典傳說,被奉為圭臬。
當(dāng)設(shè)計(jì)環(huán)路的補(bǔ)償器時(shí),我們?cè)诒M可能提高帶寬的同時(shí),不可能再刻意壓低其他部分頻段的增益,因此,用這句話作指導(dǎo)性的設(shè)計(jì)方向仍然是有意義的。
-
反饋系統(tǒng)
+關(guān)注
關(guān)注
0文章
28瀏覽量
10273 -
補(bǔ)償器
+關(guān)注
關(guān)注
0文章
87瀏覽量
14565 -
二階系統(tǒng)
+關(guān)注
關(guān)注
1文章
16瀏覽量
9719
發(fā)布評(píng)論請(qǐng)先 登錄
PLL中濾波器帶寬和環(huán)路帶寬的關(guān)系是什么?
如何用MATLAB進(jìn)行仿真得出信噪比,帶寬和信道容量的關(guān)系
談一談對(duì)穿越頻率的理解
帶寬和增益帶寬,帶寬的種類,帶寬是什么意思
LoRa的帶寬、頻率測(cè)試
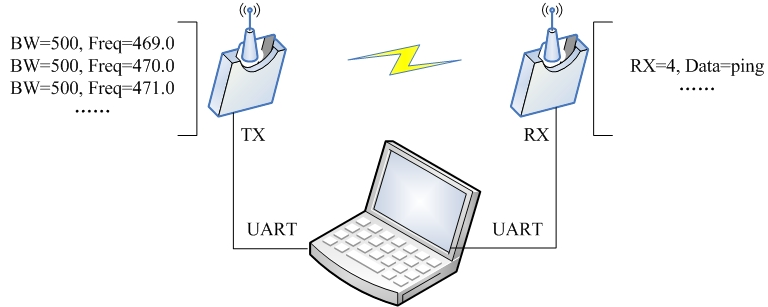
一文看懂載波頻率和帶寬的關(guān)系

帶寬和數(shù)據(jù)傳輸速率有什么關(guān)系
介質(zhì)濾波器帶寬和頻率關(guān)系大嗎_介質(zhì)濾波器調(diào)試
如何區(qū)分模擬帶寬和數(shù)字實(shí)時(shí)帶寬?
運(yùn)放帶寬與增益的關(guān)系是什么?
示波器帶寬與探頭帶寬的關(guān)系揭秘






 穿越頻率,帶寬和動(dòng)態(tài)的關(guān)系
穿越頻率,帶寬和動(dòng)態(tài)的關(guān)系











評(píng)論