1. 簡介
在工程問題的計算中,我們經常需要處理一些離散數據的擬合問題,而最小二乘法是處理曲線擬合問題的常用方法。目前,許多軟件都提供有基于最小二乘法進行曲線擬合的功能,例如在Origin和Excel中均可直接利用離散數據進行曲線擬合。然而,這些軟件只能處理一些簡單函數的擬合問題,當需要擬合的函數較為復雜時,或者無法用簡單的表達式來表述時,則往往無法直接進行擬合。為此,本文將對最小二乘法的基本原理做簡單介紹,隨后介紹如何利用Matlab的lsqnonlin函數處理復雜函數的擬合問題。
1.1 曲線擬合的最小二乘法原理
利用最小二乘法進行曲線擬合的本質為尋找某個近似函數 φ ( x ),使得該函數與離散點之間盡可能地逼近。若將偏差定義為近似函數的近似值 φ ( xi )與離散點 yi *之間的差值:

求解上述線性方程組即可得到擬合多項式的系數。
2. 利用Matlab處理曲線擬合問題
基于上述計算原理,Matlab提供了polyfit函數用于處理多項式曲線的擬合問題,對于一些較為復雜但仍可通過簡單表達式進行表述的函數,也可以利用Matlab的擬合工具箱(Curve fitting)進行擬合。但在某些情況,當擬合函數非常復雜,以致于無法用簡單表達式進行表述時(例如分段函數以及涉及到條件語句),則無法使用擬合工具箱進行擬合。對于此類問題,可以使用Matlab優化工具箱中的lsqnonlin函數進行解決。
2.1 lsqnonlin函數
lsqnonlin函數用于求解以下述形式表示的非線性最小二乘法擬合問題:
在使用該函數進行最小二乘法擬合時,lsqnonlin函數并不需要用戶提供min || f ( x )||(平方和),而是需要用戶提供自定義函數fun,用于計算矢量形式表示的 f ( x ):
lsqnonlin函數常用語法為:
x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
其中fun為用戶自定義函數,x0為計算采用的初始值,lsqnonlin函數首先利用x0通過自定義函數fun計算 fi (x)的取值并計算平方和,隨后通過優化算法調整x的取值直至得到平方和的最小值。此外,lb和ub還可以用于定義x的取值范圍,使得x滿足lb≤x≤ub。
例如,對于節1.1中所述的多項式,根據最小二乘法的定義,則自定義函數 f ( x )應表示為:
注意此時 f ( x )中的x為以向量形式表示的多項式 P ( x )的系數:
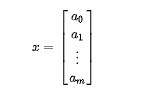
在計算時,用戶需要指定多項式系數的初始值,則lsqnonlin函數將利用最小二乘法計算多項式系數。
下面,本文將以筆者所在領域常用的NASGRO方程為例,介紹如何利用lsqnonlin函數處理此類復雜函數的曲線擬合問題。
2.2 NASGRO方程簡介
在進行基于斷裂力學的損傷容限分析時,應力強度因子和裂紋擴展速率模型是最為重要的輸入。一般來說,應力強度因子可以通過經驗公式或數值方法進行計算,而裂紋擴展速率模型則需要通過裂紋擴展速率試驗獲得的試驗數據擬合得到。例如,大量的試驗結果表明,在裂紋擴展的中速率區域,應力強度因子幅值ΔK和裂紋擴展速率d a /dN滿足良好的對數線性關系,可以通過Paris公式進行描述:
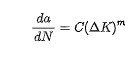
其中C和m為材料常數。
盡管Paris公式已經得到廣泛的應用,但是Paris公式僅僅描述了裂紋在中速率區域的擴展行為,沒有描述近門檻區域和接近斷裂的高速率區域的擴展行為,也沒有考慮應力比R和裂紋閉合效應對裂紋擴展速率的影響,因此給出的計算結果將過于保守。另一個常用的裂紋擴展速率模型為Newman提出的NASGRO模型,該模型基于Forman模型改進了裂紋擴展速率模型,同時比Paris和Walker模型更加全面,不僅考慮了應力強度因子門檻值和斷裂韌度,還體現了應力比以及裂紋閉合效應對裂紋擴展速率d a /dN的影響,如圖2.1所示,其表達式如下:
其中R為應力比,ΔK為應力強度因子幅值,ΔKth為應力強度因子幅值門檻值,Kmax為最大應力強度因子,可表示為:

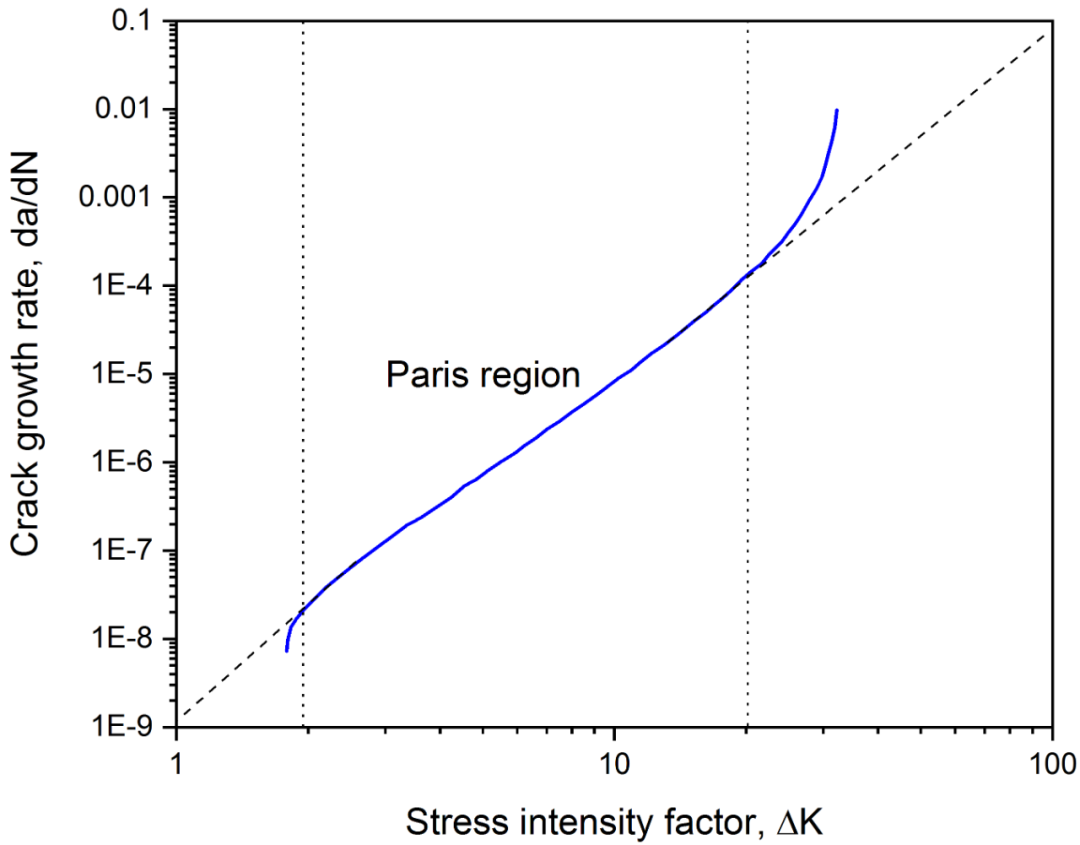
圖2.1 NASGRO方程
NASGRO方程中的應力強度因子門檻值ΔKth可采用下面的經驗公式進行估算:
其中A0為裂紋張開函數中的多項式系數,ΔK1是 R =1時的應力強度因子門檻值,Cth是對于正應力(上標為p=positive)和負應力比(上標為m=minus, negative)取不同值的材料常數,*a*~0~是內在小裂紋尺寸(典型值為0.0381mm)。在基于NASGRO方程開發的疲勞裂紋擴展分析軟件NASGRO中,正應力比下*C*~th~^p^和Δ*K*~1~是保存在數據庫里的值,負應力比下*C*~th~^m^的默認值為0.1。
2.3 NASGRO方程擬合
圖2.2為疲勞裂紋擴展分析軟件NASGRO材料庫中某鋁合金材料的裂紋擴展速率數據,已知試驗時采用的試樣為中心平板試樣(M(T)),σmax和σF的比值為0.3,塑性約束因子α為2.0,材料斷裂韌度Kc為65.7,應力比R為1時的門檻值ΔK1為1.23,C th ^p^為1.06,C th ^m^為0.1,下面需要通過擬合試驗數據獲得NASGRO方程的參數 C , m , p , q 。
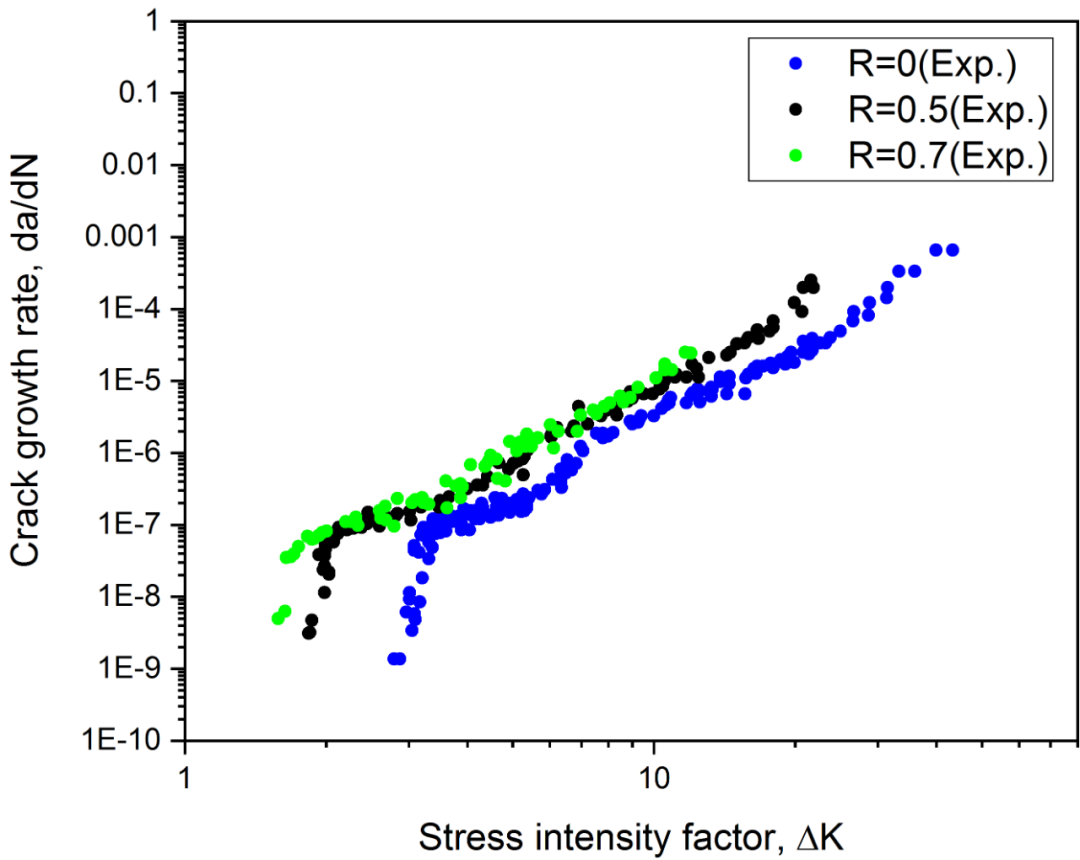
圖2.2 疲勞裂紋擴展數據
擬合NASGRO方程的難點主要有以下幾點:
(1)裂紋擴展速率d a /dN不僅與應力強度因子幅值ΔK有關,還與使用的應力比R有關,因此實際上為多變量的擬合問題;
(2)裂紋張開函數f為分段函數,并且使用了計算最大值的max函數,該函數在擬合時無法用簡單函數進行表述。
針對以上問題,NASGRO軟件給出的擬合方法為首先給參數p和q確定一個初始值,并利用最小二乘法確定參數C和 m ,隨后根據工程經驗來獲得可接受的結果,如果對擬合效果不滿意,可以調整任意參數,直至獲得滿意的結果。
顯然,這樣的擬合策略具有很大的隨意性,如果參數p和q選取不當,很可能對擬合效果有很大的影響。下面,本文將介紹如何利用lsqnonlin函數在不提前定義參數p和q的情況下對NASGRO方程進行擬合。
根據lsqnonlin函數的介紹,首先需要構造自定義函數 f ( x )使其滿足最小二乘法計算的基本原理,由于Paris公式具有對數線性的關系,因此嘗試將NASGRO方程兩邊取對數,可得:
上式可以用如下所示的通式表示:
系數bj為與 C , n , p和q有關(b 0 =log( C ), b 1 = n , b 2 = p , b 3 =- q )的系數,而gj為與Δ K 、R和NASGRO中所有剩余參數有關的函數。
根據最小二乘法的定義,應選取參數bj使得:
參考lsqnonlin函數對目標函數的定義,則自定義函數 f ( x )應表示為:

y= R .^2 * (R >0) + R * (R <= 0)
而裂紋張開函數f中涉及到求取最大值的計算以及分段函數的處理,也可以通過上述語法實現,具體的計算過程可參見程序代碼(參見附錄)。
此外,由于自定義函數 f ( x )為關于系數 bj ( j =1,2,3,4)的函數,為了將試驗數據(不同應力比R下的應力強度因子幅值ΔK和裂紋擴展速率d a /d N )傳遞到函數 f ( x )中進行計算,可以將試驗數據定義為全局變量,以便被 f ( x )調用。
通過編寫程序,可以計算得到NASGRO方程的系數如表1所示。

擬合曲線與試驗數據如圖2.3所示。
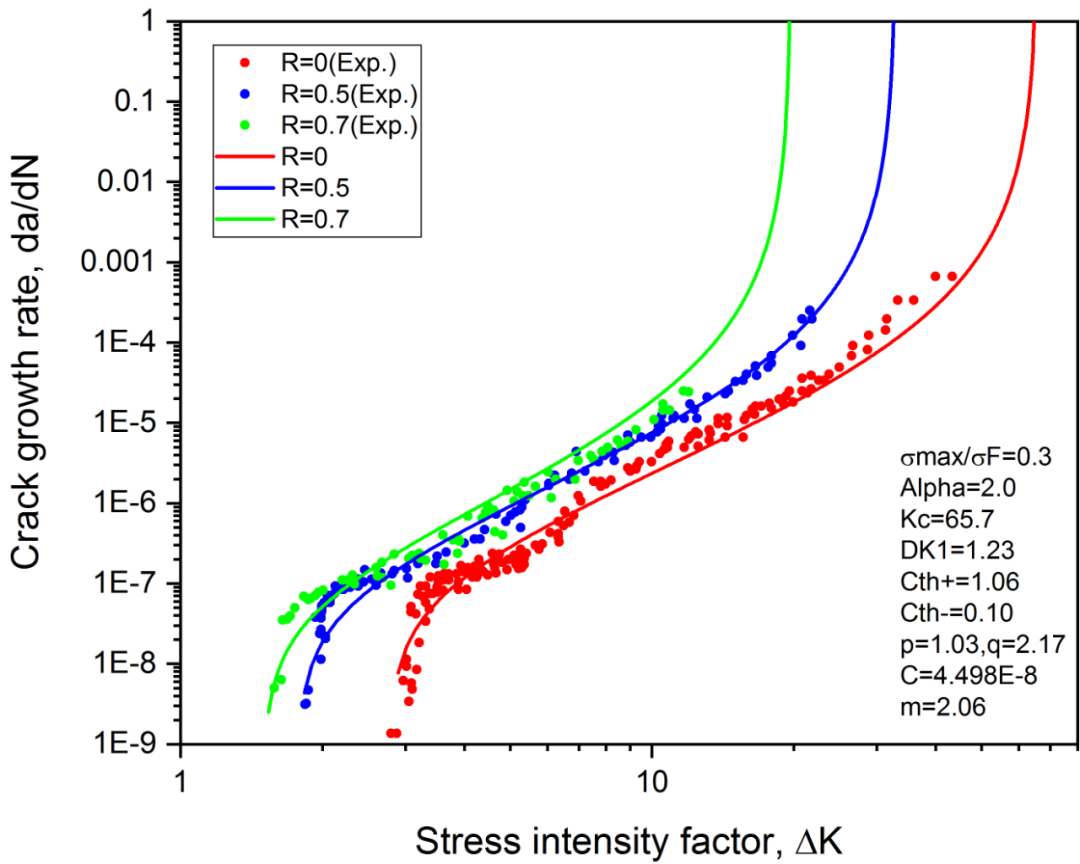
圖2.3 試驗數據及擬合曲線對比
附錄1 NASGRO方程曲線擬合程序
NASGRO_LSQ.m
NASGRO_LSQ用于定義采用最小二乘法擬合NASGRO方程時的自定義函數 f ( x ),輸入參數Coeff為NASGRO方程系數 bj ,輸出參數為擬合函數與試驗數據誤差的平方和。
function F=NASGRO_LSQ(Coeff)
%程序用于計算最小二乘法擬合NASGRO方程的目標函數
%程序返回一個N×1的數值,其中N為數據對的個數
%Coeff為擬合時待求的系數(共4個系數)
%4個系數分別為log(C)、n、p和-q
%DataX(:,1)為應力強度因子幅值
%DataX(:,2)為應力比
%DataY為裂紋擴展速率
%*********全局變量傳遞**************
global S_max_flow alpha DKth1 a0 Cth_p Cth_m a Kc
global DataX DataY
%S_max_flow為施加的最大應力與流動應力的比值
%alpha為塑性約束因子
%DKth1為應力比為1時對應的門檻值
%a0為與門檻值有關的常數
%Cth_p為正應力比下與門檻值有關的常數
%Cth_m為負應力比下與門檻值有關的常數
%a為計算門檻值時使用的裂紋長度,建議取為遠大于a0的值
%Kc為材料斷裂韌度
%DataX為應力強度因子幅值
%DataY為裂紋擴展速率
%***********************************
%********Newman裂紋張開函數計算**********
R=DataX(:,2); %應力比
DK=DataX(:,1); %應力強度因子幅值
%計算系數A0(與應力比和應力強度因子幅值無關)
A0=(0.825-0.34*alpha+0.05*alpha^2)*...
(cos(pi/2*S_max_flow))^(1/alpha);
A1=(0.415-0.071*alpha)*S_max_flow;
A3=2*A0+A1-1;
A2=1-A0-A1-A3;
%計算向量形式的裂紋張開函數
f1=max(A0+A1*R+A2*R.^2+A3*R.^3,R);
f2=A0-2*A1;
f3=A0+A1*R;
f=f1.*(R >=0)+f2.*(R< -2)+...
f3.*(R >=-2&R< 0); %裂紋張開函數
%****************************************
%********應力強度因子門檻值計算**********
DKth_p1=DKth1*sqrt(a/(a+a0))*((1-R)./(1-f)).^(1+R*Cth_p)./...
(1-A0).^((1-R)*Cth_p); %正應力比下的門檻值
DKth_p2=DKth1*sqrt(a/(a+a0))*((1-R)./(1-f)).^(1+R*Cth_m)./...
(1-A0).^(Cth_p-R*Cth_m); %負應力比下的門檻值
DKth=DKth_p1.*(R >=0)+...
DKth_p2.*(R< 0); %應力強度因子門檻值
%****************************************
%******根據NASGRO方程計算函數F***********
F1=log10((1-f)./(1-R).*DK); %DataX(1,:)為應力強度因子幅值
F2=log10(1-DKth./DK);
F3=log10(1-1./(1-R).*(DK./Kc));
%****************************************
%******根據NASGRO方程計算裂紋擴展速率***********
y=Coeff(1)+Coeff(2)*F1+Coeff(3)*F2+Coeff(4)*F3;
%***********************************************
%*****構造基于最小二乘法的目標函數F**************
%最小二乘法應保證目標函數F中所有原始之和達到最小
F=(y-log10(DataY)).^2;
%***********************************************
end





 如何利用Matlab的lsqnonlin函數處理復雜函數的擬合問題
如何利用Matlab的lsqnonlin函數處理復雜函數的擬合問題