
very amazing啊,這說明什么,這說明我們想要實現 t-product積 不用費勁的去搞循環矩陣,也不用去搞什么分塊展開再折疊,我們要做的只是, 傅立葉變換--相乘--傅立葉逆變換 !!!
** PART.1 流程講解**
原本的t-QR分解流程:

** PART.2 MATLAB實現**
原始版本t-product
function C=t_prod(A,B)
% @author:slandarer
% 用于進行張量t-product積
% A*B=fold(bcirc(A)·unfold(B))
% 獲取張量大小
[l,p,n]=size(A);dimA=[l,p,n];
[p,m,n]=size(B);dimB=[p,m,n];
dimC=[l,m,n];
if dimA(2)~=dimB(1) || dimA(3)~=dimB(3)
error('Inner tensor dimensions must agree.');
end
% 對A,B進行unfold展開操作
ufold_A=reshape(permute(A,[2,1,3]),dimA(2),[])';
ufold_B=reshape(permute(B,[2,1,3]),dimB(2),[])';
% 對A構建循環矩陣
bcirc_A=zeros([l*n,p*n]);
for i=1:n
bcirc_A(:,(1:p)+(i-1)*p)=circshift(ufold_A,l*(i-1),1);
end
% bcirc(A)·unfold(B)
AB=bcirc_A*ufold_B;
% 還原張量維度
C=ipermute(reshape(AB',dimC([2,1,3])),[2,1,3]);
end
fft版本t-product
function C=t_prod_fft(A,B)
% @author:slandarer
% 基于快速傅立葉變換的張量t-product積
if size(A,2)~=size(B,1) || size(A,3)~=size(B,3)
error('Inner tensor dimensions must agree.');
end
fftA=fft(A,[],3);
fftB=fft(B,[],3);
fftC=zeros([size(A,1),size(B,2),size(A,3)]);
for i=1:size(A,3)
fftC(:,:,i)=fftA(:,:,i)*fftB(:,:,i);
end
C=ifft(fftC,[],3);
end
比較測試
% test t-product
addpath('.t_product')
A=zeros(2,3,3);
A(:,:,1)=[1 2 3; 3 4 5];
A(:,:,2)=[5 6 7; 7 8 9];
A(:,:,3)=[9 10 11;11 12 13];
B=zeros(3,2,3);
B(:,:,1)=[1 2; 3 4; 5 6];
B(:,:,2)=[5 6; 7 8; 9 10];
B(:,:,3)=[9 10;11 12;13 14];
tic
C1=t_prod(A,B)
toc
tic
C2=t_prod_fft(A,B)
toc
C1(:,:,1) =
438 492
564 636
C1(:,:,2) =
438 492
564 636
C1(:,:,3) =
294 348
420 492
歷時 0.005764 秒。
C2(:,:,1) =
438 492
564 636
C2(:,:,2) =
438 492
564 636
C2(:,:,3) =
294 348
420 492
歷時 0.001014 秒。
可以發現結果完全相同,而fft版本代碼更簡短,而且因為省去了循環矩陣創建等操作,運行速度也相較于原始版本更快。
-
比較器
+關注
關注
14文章
1841瀏覽量
108609 -
FFT
+關注
關注
15文章
444瀏覽量
60670 -
MATLAB仿真
+關注
關注
4文章
176瀏覽量
20316 -
傅立葉變換
+關注
關注
3文章
105瀏覽量
32799
發布評論請先 登錄
介紹藍牙通信的另一種方式--BLE
大功率氙氣燈成為節能照明的另一種可能
以另一種姿態......谷歌正在以另一種方式重返中國
一種通過張量積圖擴散的醫學圖像檢索
卡博菲推出了另一種創新的安裝方式:整合配線架安裝
轉換器(converter)是指將一種信號轉換成另一種信號的裝置
所有行業的數據采集:雙極性輸入的另一種配置
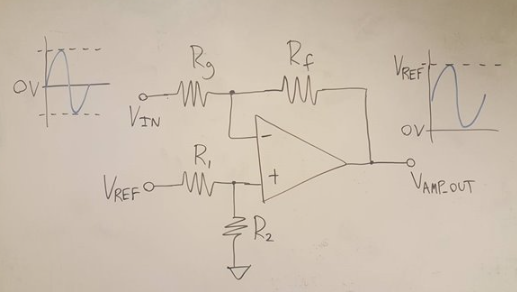





 張量t-product積還有另一種實現方式?
張量t-product積還有另一種實現方式?












評論