如何控制使用長輸出線時的傳導 EMI（中）

簡介

本文為分析并改善長線負載下過高傳導EMI問題系列文章之中篇。上篇回顧了共模 (CM) EMI 模型，并考慮了電場耦合和磁場耦合的影響；中篇將利用一系列公式來探討傳輸線對輸出長線對地阻抗的影響；下篇將總結三種 EMI 降噪方法，同時分析和預測諧振峰值。

輸出長線對地阻抗

如果輸出線較長，在傳導的高頻頻段，我們需要考慮它的傳輸線效應。電力電子工程師朋友們在日常工作中可能很少會用到這部分的內容，因此首先介紹一下相關的概念。

當電路尺寸與要考察的頻率對應的波長相近時，電路的相關參數，如電壓、電流、阻抗等，會由集中參數變為分布參數。

對于傳輸線的每一小段，如圖 1所示，我們可以考察它的單位電感、電阻、電容以及電導。

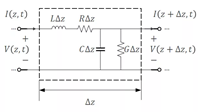
圖1: 傳輸線模型

傳輸線上的電流和電壓分布可以用公式（1）來計算：

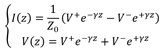
其中Z0為傳輸線的特征阻抗，γ為傳輸常數。當傳輸線上的損耗（如圖1中的R和G）可以忽略不計時，Z0可以用公式（2）來估算：

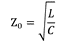
而γ可以用公式（3）來計算：

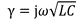
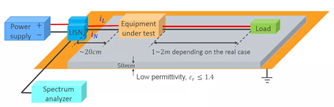
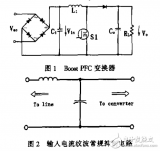
圖2顯示出輸出線所具有的幾何形狀，這意味著我們可以利用電磁場理論來求得參數。

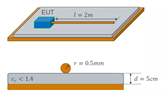
圖 2：輸出線對地的幾何模型

如若忽略損耗，則可以使用公式 (4) 估算電容：

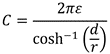
其中d代表傳輸線與參考地之間的距離，r為傳輸線的半徑，ε為介質的介電常數。系統電感可以用公式 (5) 計算：

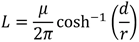
其中μ為介質的磁導率。這里因為是共模噪聲，所以輸出的兩條線近似合并為同一導體考慮。

由于我們的輸出線的末端與參考地之間沒有連接，可以認為是近似開路（末端電流為0），我們可以將（2）-（5）代入到（1），得到最終輸出線上的電流與電壓表達式。因此，可以得到，對于長度為l的輸出線，它的阻抗(ZOC)可以用（6）表示：

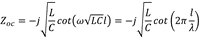
其中ω為角頻率(2πf)；而λ即為波長(1 / (f x (√LC))。

通過（6），根據三角函數的性質，在l為四分之一波長的奇數倍時（如1/4λ，3/4λ等），這個阻抗將發生串聯諧振，導致EMI傳播路徑上的阻抗大幅減小，因此，我們會發現有EMI峰的存在。如果傳輸線長為2m，那么根據我們的實際情況，1/4λ，3/4λ對應的頻率分別在31.6MHz和95.1MHz，這也就解釋了為什么上篇圖3的頻譜上會出現這兩個峰。

這個理論也很容易直接通過測量進行驗證。圖3為不同長度傳輸線的對地阻抗測量結果，顯然，對于2m的輸出線，其阻抗謝振峰的位置符合我們之前的計算結果，這也解釋了EMI測量結果中的諧振峰。另外，輸出線越短，諧振發生的頻率也越高。

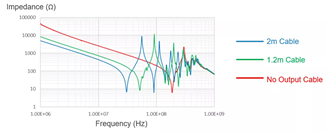
圖 3：不同長度的傳輸線接地阻抗測量結果

最后，對應1/4λ的頻率可以使用公式 (7) 進行估計：

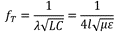
通過上式可以確認，輸出線與參考地之間的距離以及線徑不會影響諧振的位置，諧振只與輸出線的長度有關。

結論

在本文中，通過計算電流和電壓的分布、傳輸線損耗、電感、電容、最終輸出線阻抗和頻率，我們得到了上篇中描述的CM EMI模型。在下篇中，我們將分析多種降噪方法的效果，并最終實現長線負載的成功輸出。

審核編輯：湯梓紅