1

反相放大電路

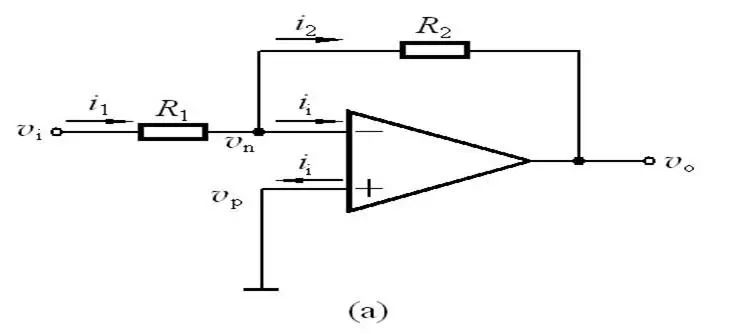
圖中運放的同向端接地Vp=0V，反向端和同向端虛短，所以也是0V，反向輸入端輸入電阻很高，虛斷，幾乎沒有電流注入和流出，那么R1和R2相當于是串聯的，流過一個串聯電路中的每一只組件的電流是相同的，即流過R1的電流和流過R2的電流是相同的。

I1 = (Vi - V-)/R1 ................a

I2 = (V- - Vout)/R2 ............b

V- = V+ = 0 .......................c

I1 = I2 ...............................d

求解上面的初中代數方程得Vout =

(-R2/R1)*Vi

這就是我們平時所說的反向放大器的輸入輸出關系式了。

很簡單吧？既然講到了反相放大電路，很容易想到應該會有同相放大電路，那我們接著來看看同相放大電路又是怎么樣的吧。

2

同相放大電路

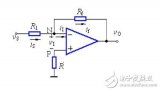
圖中Vn與Vp虛短，

則 Vp = Vn .......................a

因為虛斷，反向輸入端沒有電流輸入輸出，通過R1和R2 的電流相等，設此電流為I，由歐姆定律得：

I = Vout/(R1+R2) ............b

Vi等于R1上的分壓， 即：

Vi = I*R1 .........................c

由abc式得:

Vout = Vi*(R1+R2)/R2

這就是同向放大器的輸入輸出電壓關系了。

3

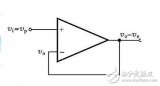
電壓跟隨器

當同相放大電路中R1 = R2 = 0 就產生了一種特殊用法，我們稱之為電壓跟隨器，很明顯，我們可以知道，它的輸入與輸出是一樣的，你可能會想，既然這樣，那我們用它有意義嗎？當然有，現實生活中任何一種應用電路都不可能憑空出現，運放電路具有輸入阻抗高，而輸出阻抗低的特性，使用一級跟隨器可以避免電路中由負載的變化而引起輸出量的變化，以使負載效應最小化。這樣在電路中它就相當于一個隔離器或緩沖器，能保證我們電路功能的穩定。可以理解吧？

4

加法電路

圖中，由虛短可知：

Vn= Vp = 0 ..................a

由虛斷及基爾霍夫定律（不知道這是啥的可以先不管或百度一下，或者類比一下中學知識并聯電路的歐姆定律）可知，通過R2與R1的電流之和等于通過R3的電流，故

(V1 – Vn)/R1 + (V2 – Vn)/R2 = (Vn –Vout)/R3 ......................b

代入a式，b式變為

V1/R1 + V2/R2 = Vout/R3

如果取R1=R2=R3，則上式變為

-Vout=V1+V2，

這就是所謂的加法器了。

有了加法電路，那肯定就少不了減法電路吧，減分電路又是怎么樣的呢？現在一起來看看。

5

減法電路

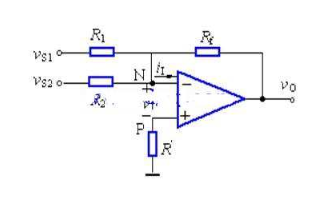
圖中由虛斷可知，通過R2的電流等于通過R3的電流，同理通過R1的電流等于R4的電流，故有

(V2 – Vp)/R2 = Vp/R3 ................a

(V1 – Vn)/R1 = (Vn - Vout)/R4 ...b

如果R2 = R3， 則

Vp = V2/2 ..................................c

如果R1 = R4， 則

Vn = (Vout + V1)/2 ....................d

由虛短知 Vn = Vp .....................e

所以 Vout = V2-V1 這就是傳說中的減法器了。

6

積分電路

圖電路中，由虛短知，反向輸入端的電壓與同向端相等。

由虛斷知，通過R的電流與通過C的電流相等。

通過R的電流

i = V1/R

通過C的電流

i = CdUc/dt = -CdVout/dt

所以

Vout = ((-1/(R*C))∫V1dt

輸出電壓與輸入電壓對時間的積分成正比,這就是傳說中的積分電路了。

若V1為恒定電壓U，則上式變換為

Vout = -Ut/(RC)

t 是時間，則Vout輸出電壓是一條從0至負電源電壓按時間變化的直線。

同樣的道理，有積分電路就有微分電路，那微分電路又是怎么樣的呢，我們一起來看看。

7

微分電路

圖中由虛斷知，通過電容C和電阻R的電流是相等的。

由虛短知，運放同向端與反向端電壓是相等的。則：

Vout = -i * R = -(R*C)dV1/dt

這是一個微分電路。

如果V1是一個突然加入的直流電壓，則輸出Vout對應一個方向與V1相反的脈沖。