電動汽車的引擎,醫學中的磁共振成像,廚房中的電熱水壺,你的智能手機的充電器,無線電,WiFi等等。任何利用電或磁的設備基本上都是基于麥克斯韋方程(Maxwell equations)的。
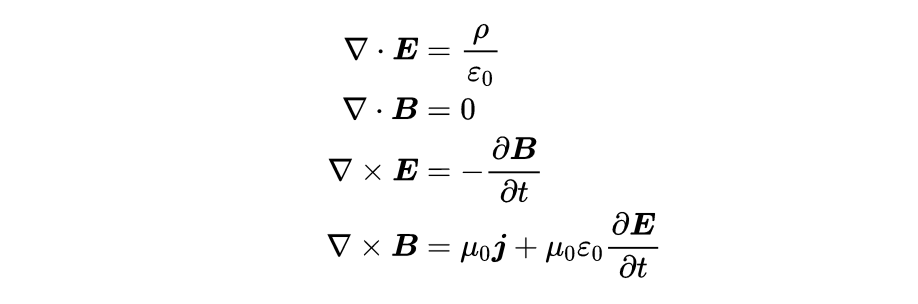
本文的目標不是理論或實驗證明麥克斯韋方程,而是盡可能簡單易懂地呈現它們。我還會解釋麥克斯韋方程中出現的數學概念。然而,首先,你應該知道什么是偏導數以及什么是積分。要理解所有的麥克斯韋方程,你還要知道什么是電場和磁場。
考慮一個帶有電荷“Q”的大電荷球和一個帶有電荷“q”的小電荷球。這兩個球體相距r,它們之間的電力由庫侖定律(coulombs law)給出。
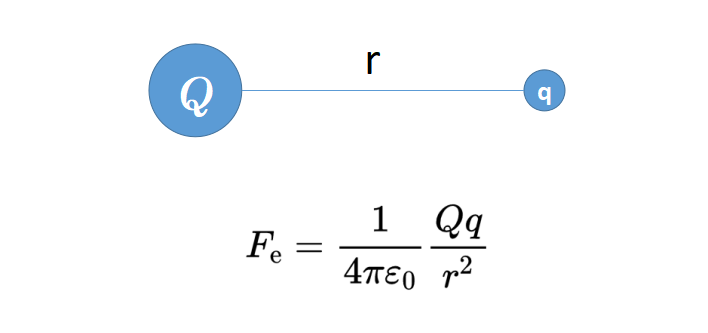
現在,如果你知道大電荷的值,想知道大電荷對小電荷施加的力的值怎么辦?但是,你并不知道這個小電荷的具體值,或者你有意將這個值保持開放,只想看大電荷(對其)施加的力。
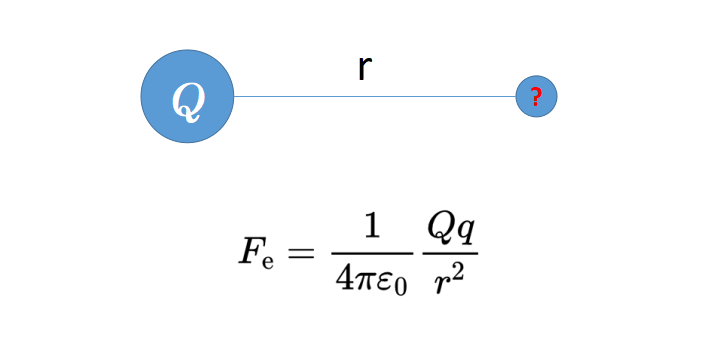
因此,你必須以某種方式從庫侖定律中消除小電荷q。為此,你只需在庫侖定律的兩邊都除以q。這樣,右邊的小電荷就消失了,反而出現在等式的左邊。
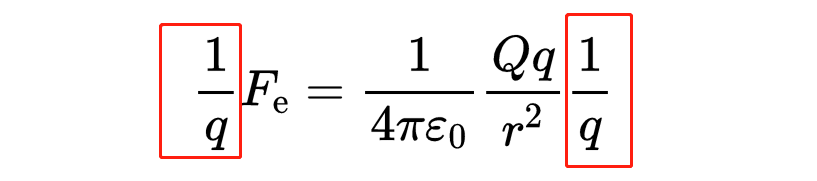
左邊“F/q”被定義為源電荷Q的電場E,(稱其為源電荷)是因為電荷Q是電場的源頭。
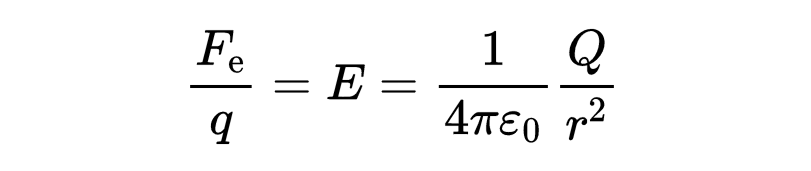
電場E因此表示在與源電荷距離r的位置放置一個小電荷時,會作用于它的電力。到目前為止,只考慮了電場的大小,即電場的強度,而沒有考慮電場的精確方向。然而,麥克斯韋方程是通用的,也包括電場的方向。因此,我們必須將電場轉化為向量。
向量以粗體顯示。手寫時,大多數人會在字母上面加一個小箭頭,以區別于標量。我省略了箭頭。三維空間的電場E作為向量具有三個部分(分量)Ex,Ey和Ez,
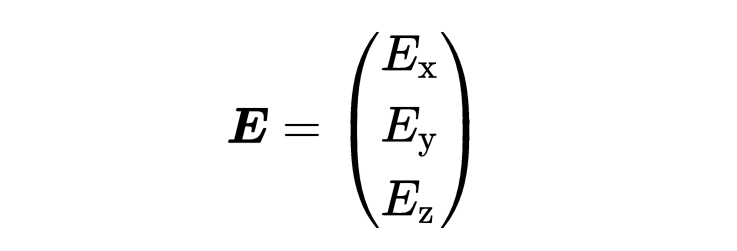
讓我們看看第一個部分。第一個部分依賴于空間坐標(x, y, z),是x方向的電場大小。也就是說,根據(x, y, z)的具體位置,Ex的值是不同的。
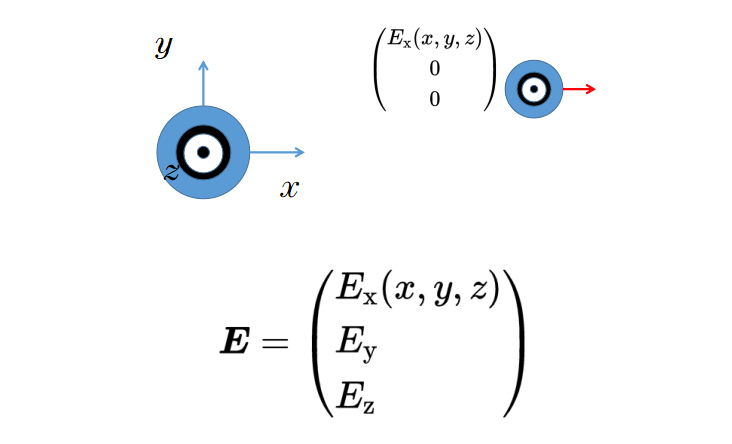
同樣的規則也適用于其它兩個部分Ey和Ez,它們分別表示y方向和z方向的電場強度。
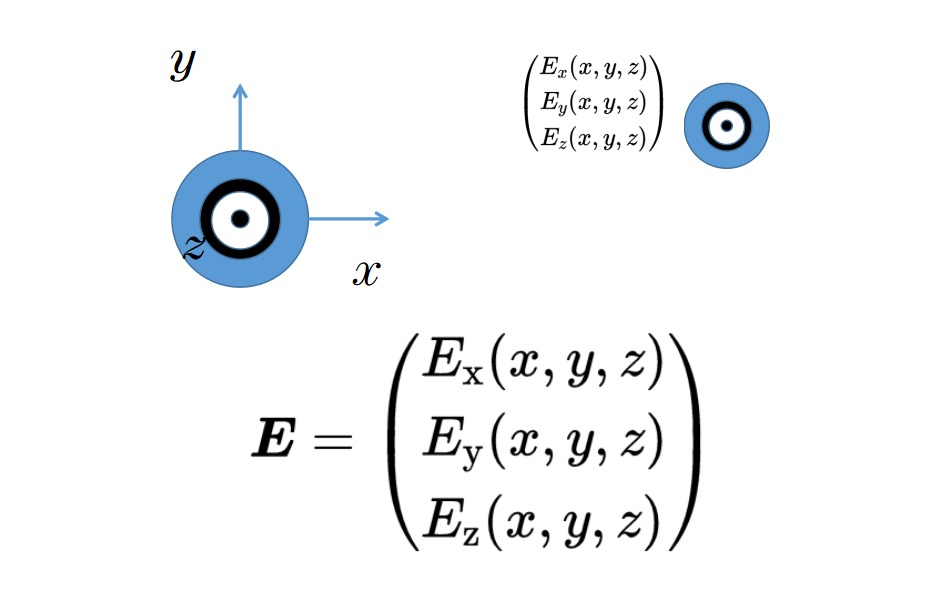
電場的分量表明在特定位置的測試電荷在第一,第二或第三個空間方向上會受到哪種電力作用。
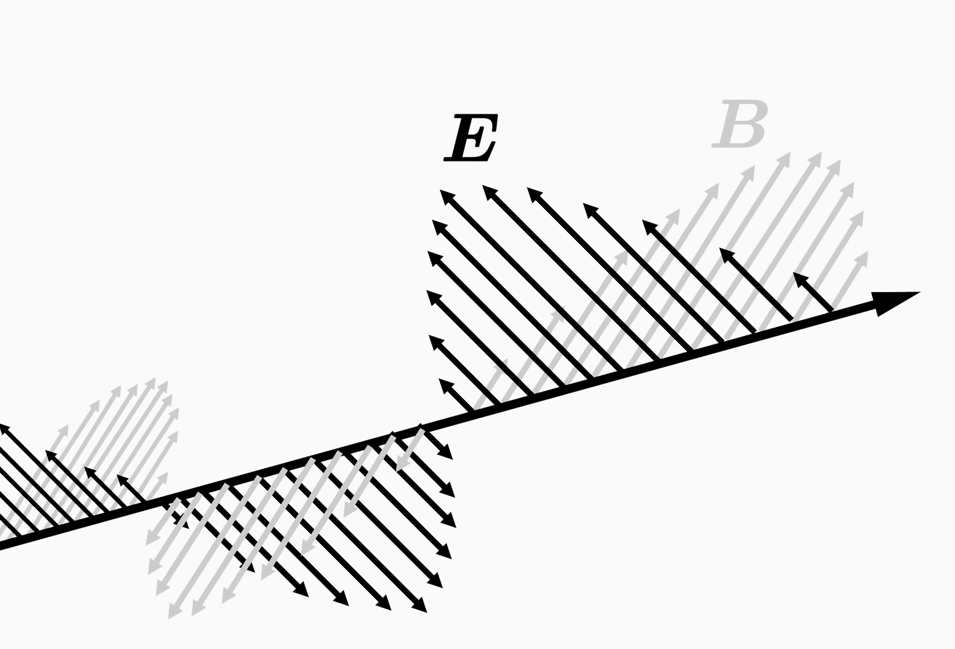
麥克斯韋方程中的另一個重要物理量是磁場B。實驗證明,一個帶有電荷q的粒子在外部磁場中以速度v移動會受到磁力的作用,這使得粒子偏離原來的路徑。粒子上的力與其電荷q和速度v成正比,也就是說,如果電荷或速度加倍,那么作用在粒子上的力也會加倍。
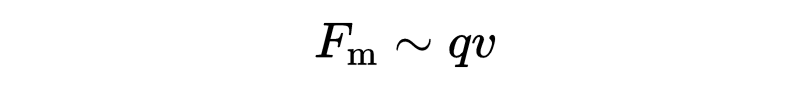
但不僅如此!力也與所施加的磁場成正比。為了描述力和磁場之間的這種比例關系,我們引入了物理量B。這個量的單位必須使得等式右邊的單位為力的單位,也就是“牛頓”或“千克米每秒平方”。
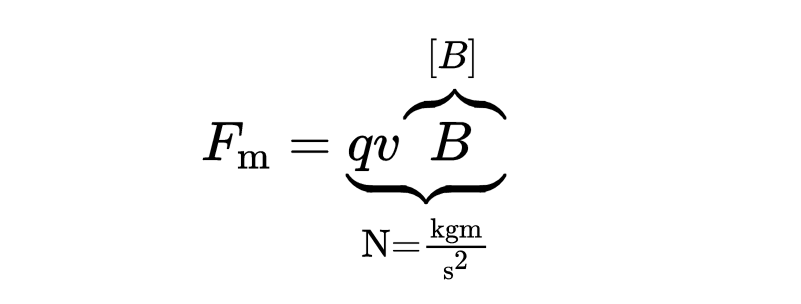
經過簡單的轉換,你會發現這個單位必須是“千克每安培秒平方”。這就是我們稱之為特斯拉(T)的單位。我們把B稱為磁通密度(或簡稱:磁場)。

磁通密度描述了外部磁場,從而決定了作用在帶電粒子上的力的大小。公式“qvB”表示帶電粒子在磁場中受到的磁力,這僅僅是力的大小。為了像電力一樣以向量的形式表達磁力,力、速度和磁場都被表示為向量形式。
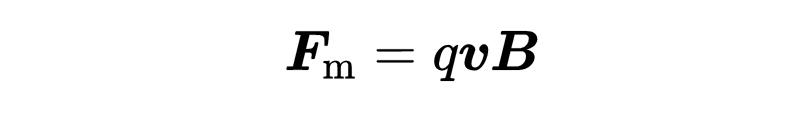
現在,這三個量不再是標量,而是具有x,y和z方向的三維向量。
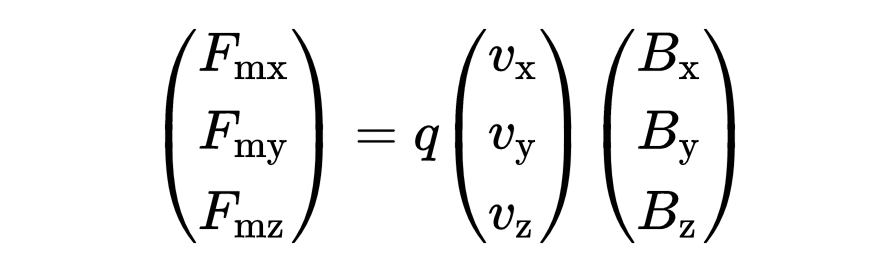
現在的問題是:速度向量v應如何與磁場向量B進行向量乘法?如果你仔細觀察磁場中電荷的偏轉,你會注意到磁力始終指向與速度和磁場線垂直的方向。這種正交性可以用所謂的叉積來運算。
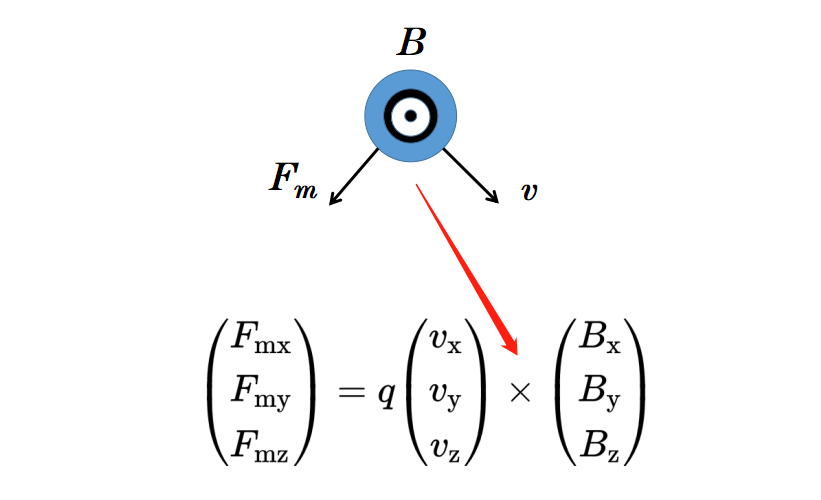
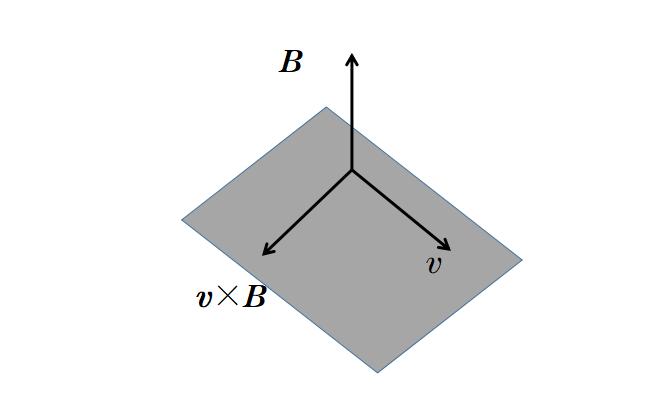
兩個向量v和B的叉積是一個向量,總是垂直于向量v和B。
第一個分量是
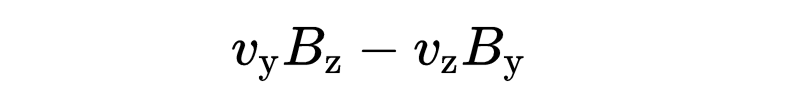
第二個分量是
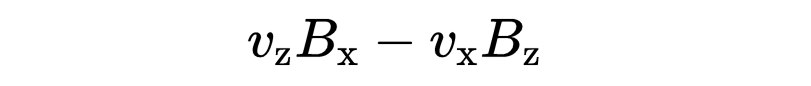
叉積的第三個分量是
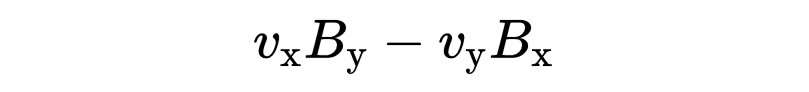
所以
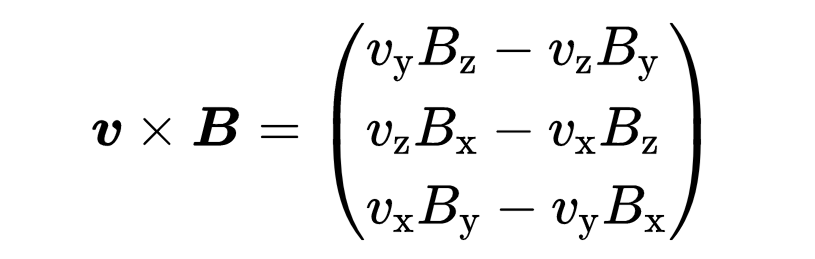
為了使力總是垂直于v和B,我們在公式中取v和B的叉積。所以磁力的向量形式一般為:
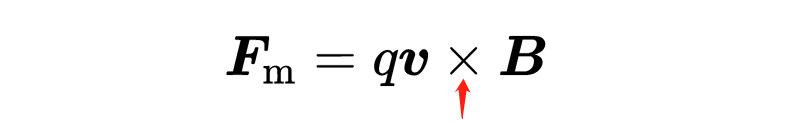
電荷q是一個普通的標量因子。正如你所看到的,物理量B描述了磁場的強度,這會導致移動的電荷發生偏轉。
現在你已經學習了麥克斯韋方程中的兩個重要物理量,即電場E和磁場B。
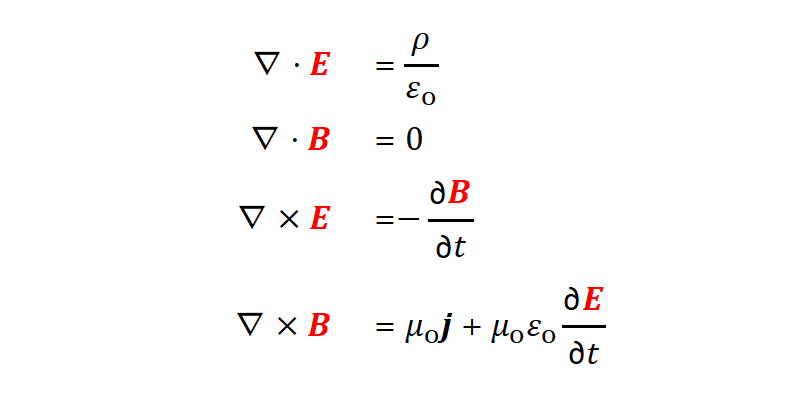
它們都是所謂的向量場。這意味著你可以將一個電場和磁場向量分別賦給空間中的每個位置(x, y, z),這兩個向量同時表示了電場和磁場的大小和方向。
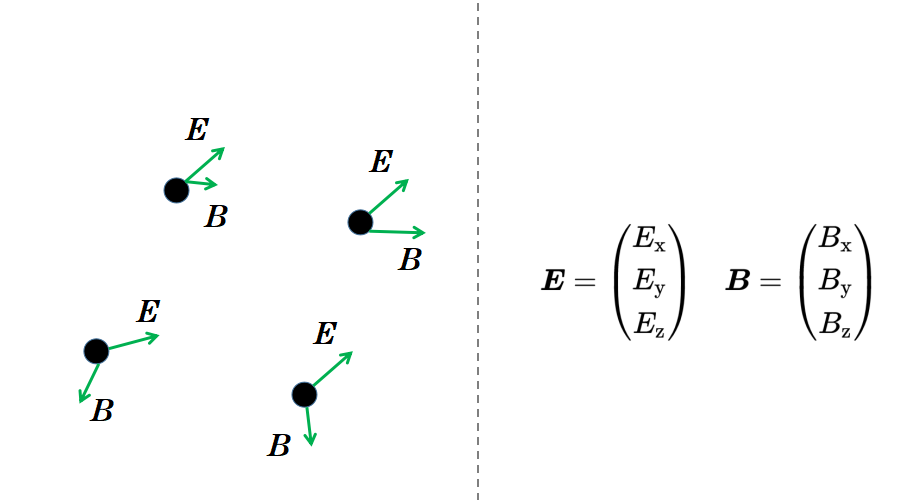
總共有四個麥克斯韋方程。這四個麥克斯韋方程可以用兩種不同的方式來表示。有所謂的積分形式,它用積分來表示麥克斯韋方程,
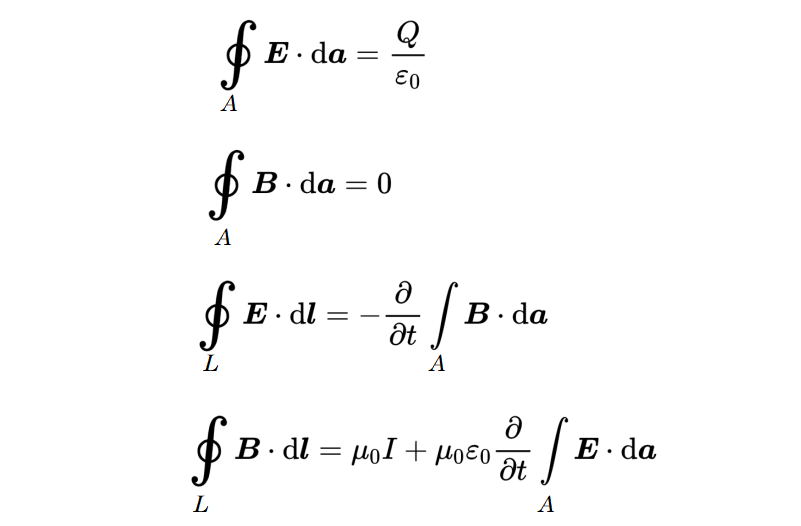
還有微分形式,它用導數來表示麥克斯韋方程:
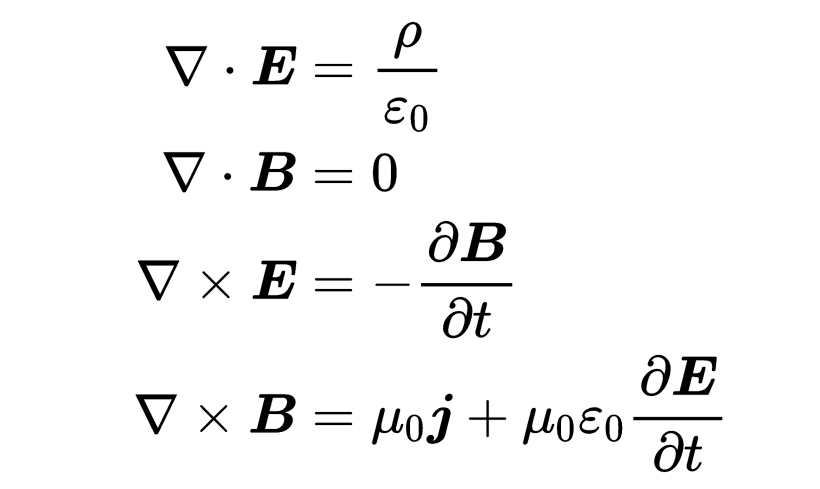
微分形式的麥克斯韋方程對于在空間的一個單點計算磁場和電場是有用的,而積分形式則用于在整個空間區域內計算場。
積分形式適用于計算對稱問題,例如計算帶電球體、帶電柱體或帶電平面的電場。
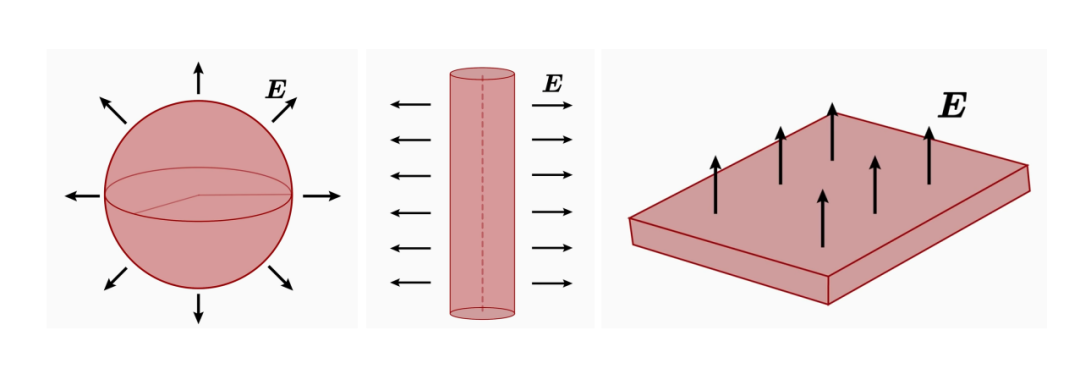
微分形式更適用于用計算機計算復雜的數值問題,或者例如,用于推導電磁波。
另外,微分形式看起來比積分形式更緊湊。兩種形式都很有用,可以通過兩個數學定理相互轉化。一個定理被稱為散度積分定理(Divergence integral theorem),另一個是旋度積分定理(curl integral theorem)。如果你理解了這兩個定理,那么你就會更容易理解麥克斯韋方程。讓我們先來看看散度積分定理。
散度定理
這是散度積分定理的完全形態:
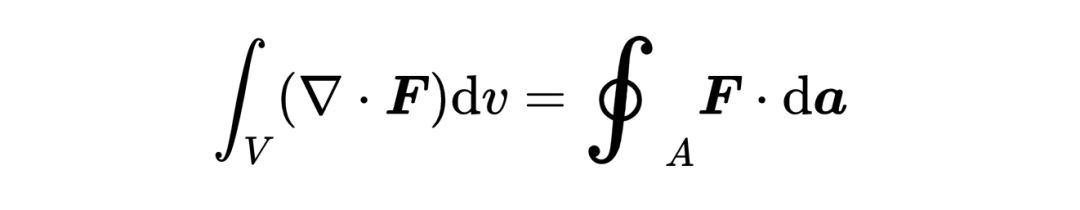
首先,讓我們看一下等式的右邊,
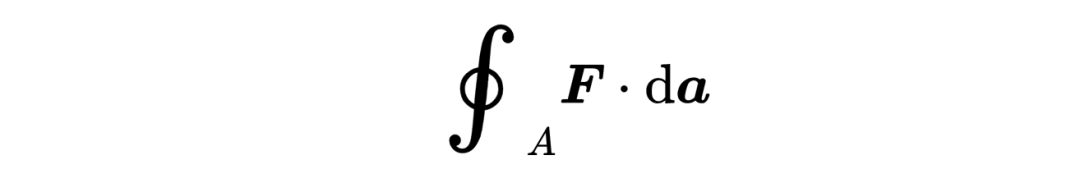
這里的A代表一個封閉任何體積的表面,例如立方體、球體或者你能想到的任何三維物體的表面。

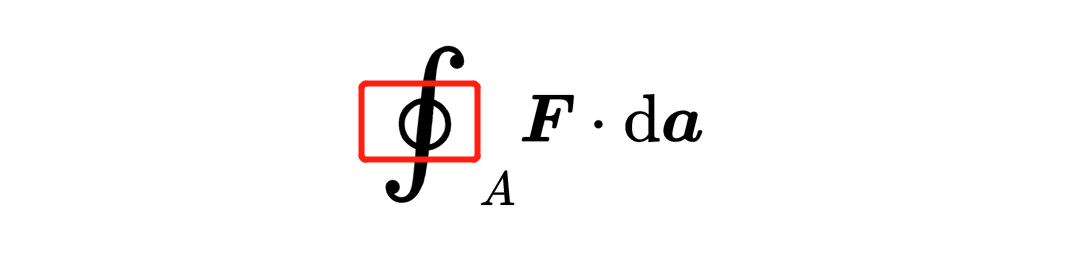
在積分符號上的小圓圈表明這個表面必須滿足一個條件:表面必須是封閉的,也就是說,它不能包含任何的孔洞,以便在數學上保證這個條件。因此,表面a就是一個封閉的表面。
這里的F是一個矢量場,可以表示電場
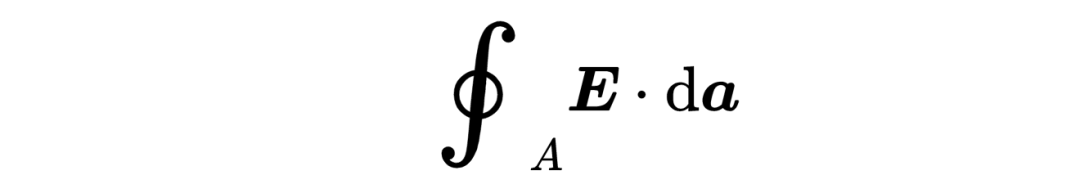
或磁場,
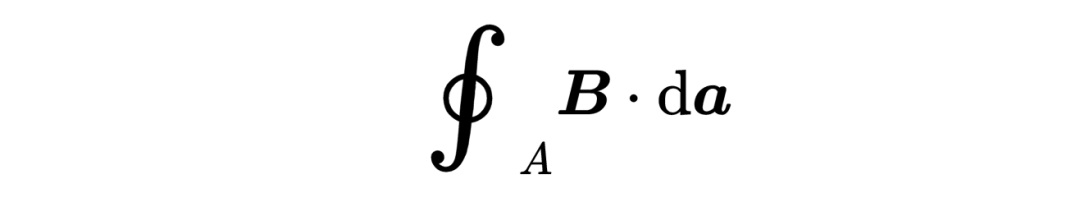
當我們在考慮麥克斯韋方程的時候,它是一個有三個組成部分的矢量,
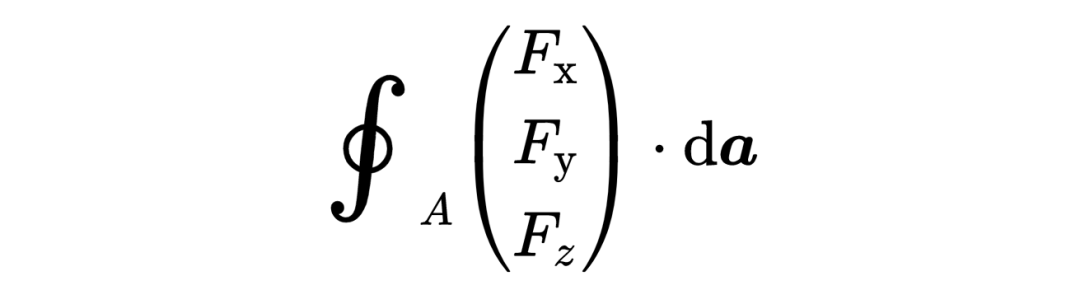
da是無窮小的表面元素,就是所考慮的表面A的無窮小表面元素。
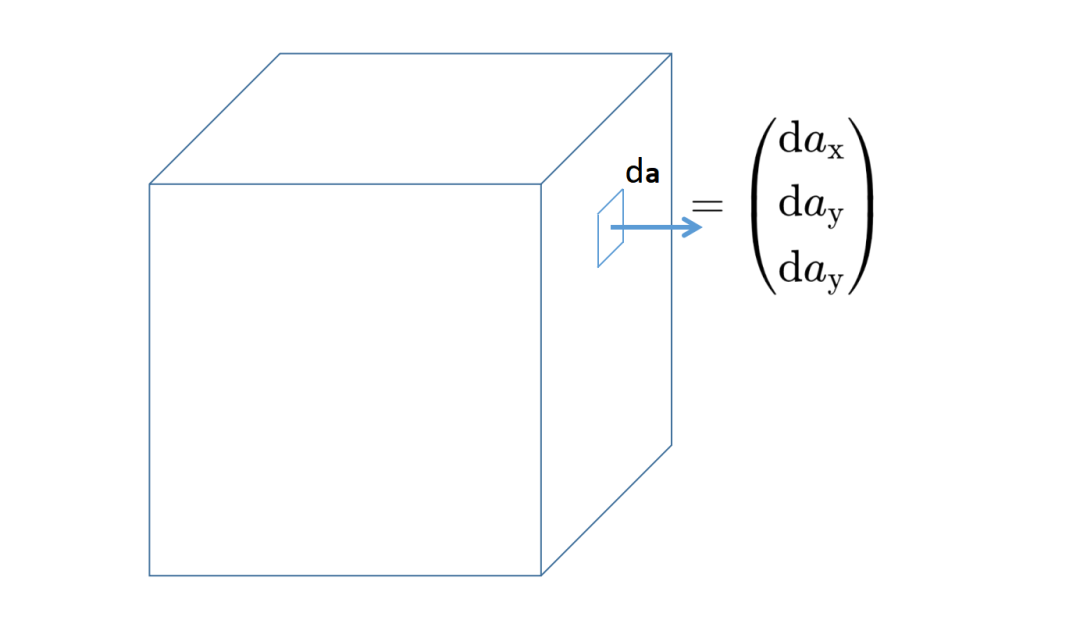
你可能已經注意到,da元素中的a是加粗的,所以它是一個有大小和方向的矢量。da元素垂直于表面,并且定義為從表面指向外部。

在矢量場和da元素之間的點代表所謂的標量積。標量積是一種乘兩個矢量的方法,所以在這里,矢量場和da元素之間的標量積是形成的。標量積的定義如下:
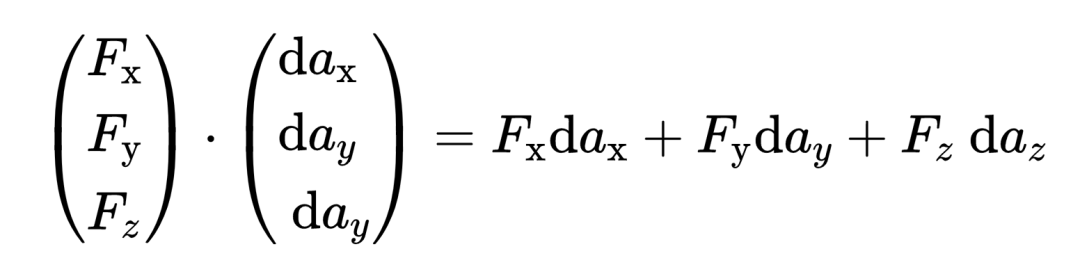
從定義中可以看出,兩個矢量的第一,第二和第三組成部分是相乘然后相加的。標量積的結果不再是一個矢量,而是一個普通的數字。
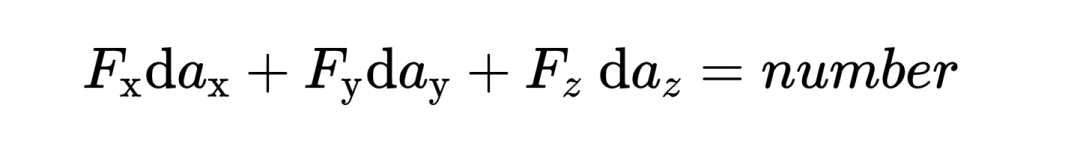
為了理解這個數字的含義,你首先要知道任何矢量都可以寫成兩個其他矢量的和,
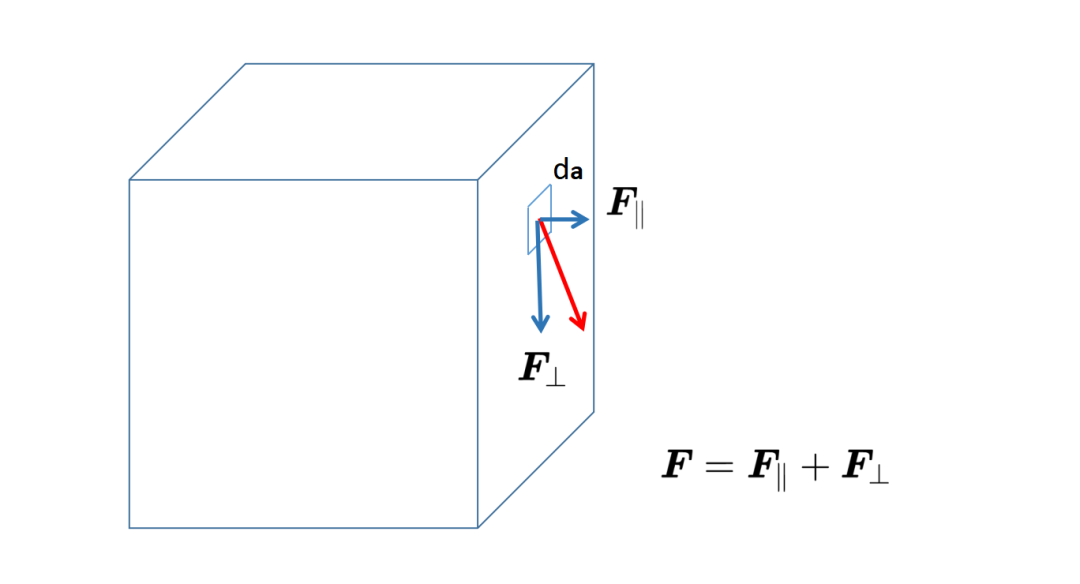
其中一個矢量平行于da元素,我們稱之為F平行,另一個矢量垂直于da元素,我們稱之為F垂直。另一個數學事實是,兩個垂直矢量的標量積總是等于零,這就意味著,
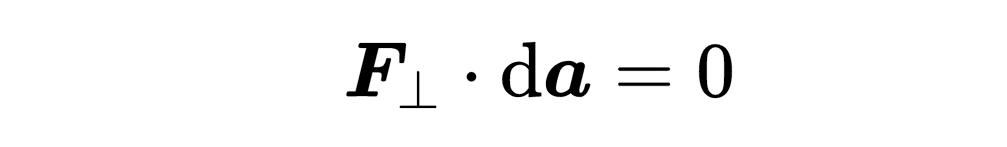
然而,F平行和da元素之間的標量積通常不是零,
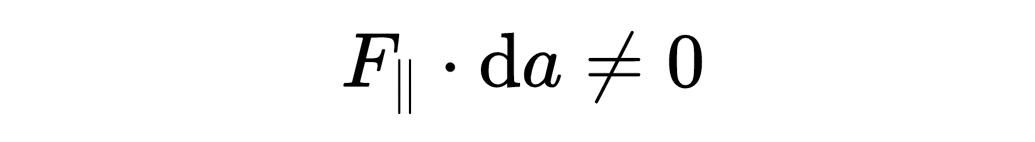
所以現在你可以看到等式右邊的標量積是怎么計算的,
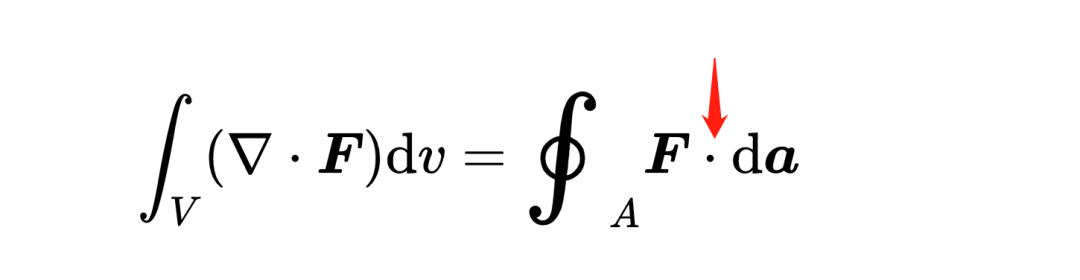
它只選擇了矢量場中和da元素平行的部分,剩下的在垂直方向上的矢量場部分被標量積消除。
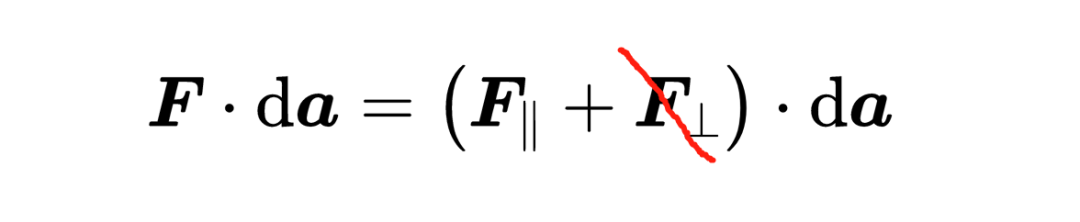
接下來,對于被考慮的表面A的所有位置,都會累加標量積,這就是積分的任務,
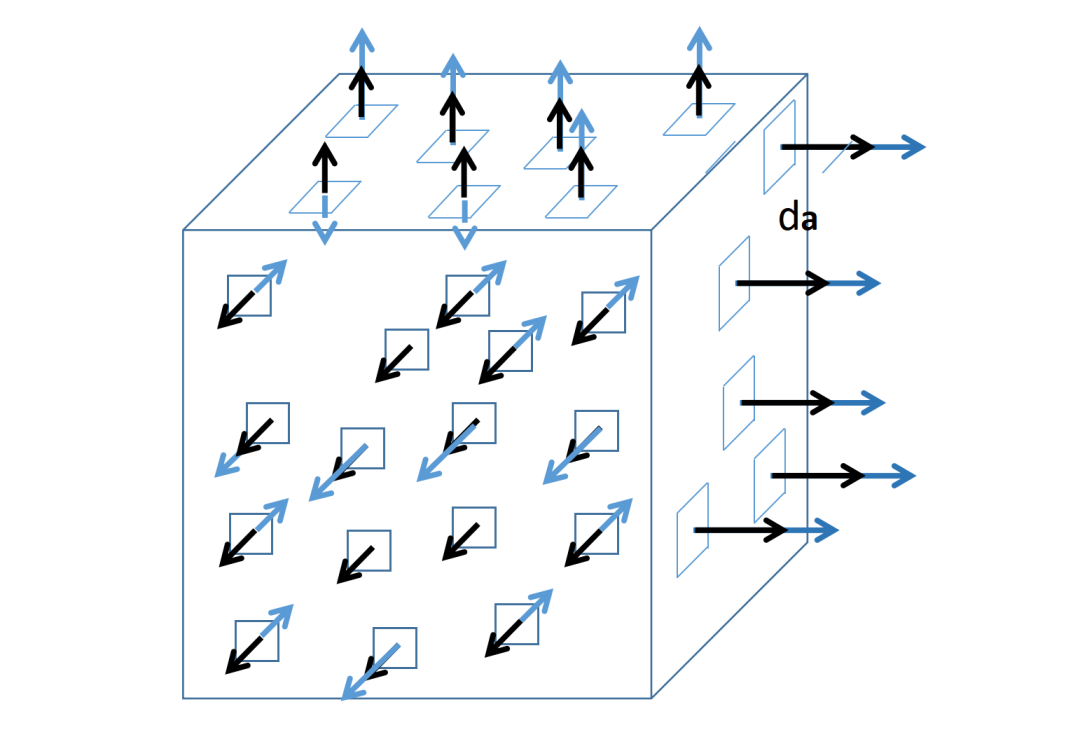
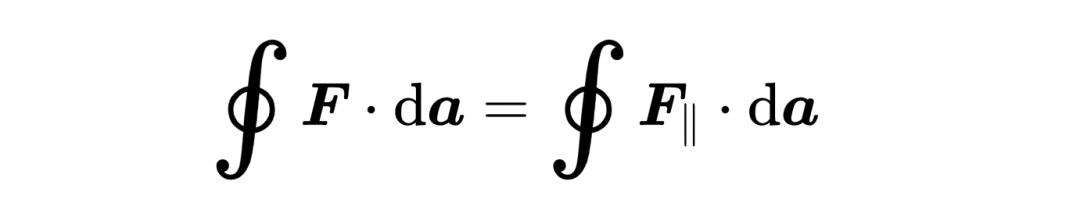
因此,散度定理的右側會求和所有流入或流出表面A的矢量場F的分量。這種對表面的小片段進行求和的積分被稱為表面積分(surface integral)。如果積分函數是一個矢量場,這個表面積分被稱為矢量場F通過表面A的流量?。
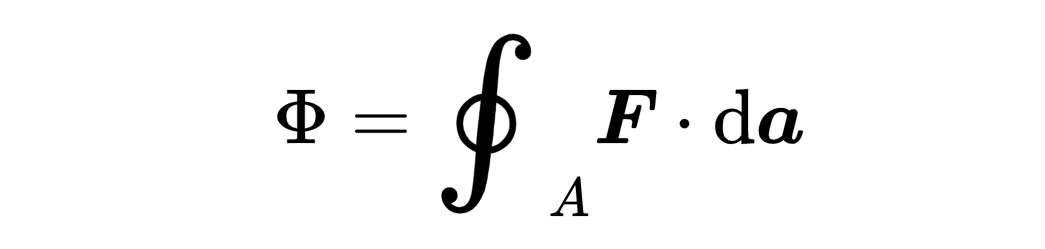
這個描述基于這個表面積分的意義,它度量了多少的矢量場F流出或流入被考慮的表面A。
如果這個表面積分的矢量場F是電場E,那么這個表面積分就被稱為通過表面A的電通量。如果矢量場F是磁場B,那么這個表面積分就被稱為通過表面A的磁通量。
現在讓我們看看定理的左側,
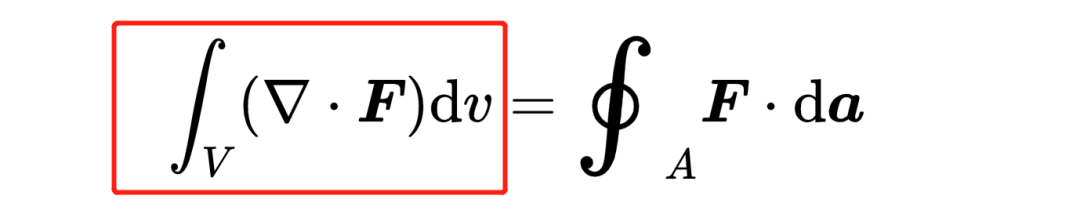
V是一個體積,它是由表面A封閉的體積。dv是一個無窮小的體積元素,換句話說,它是被考慮的體積V的無窮小的體積片段。
上下三角符號被稱為nabla算子,它有三個組成部分,就像矢量一樣,
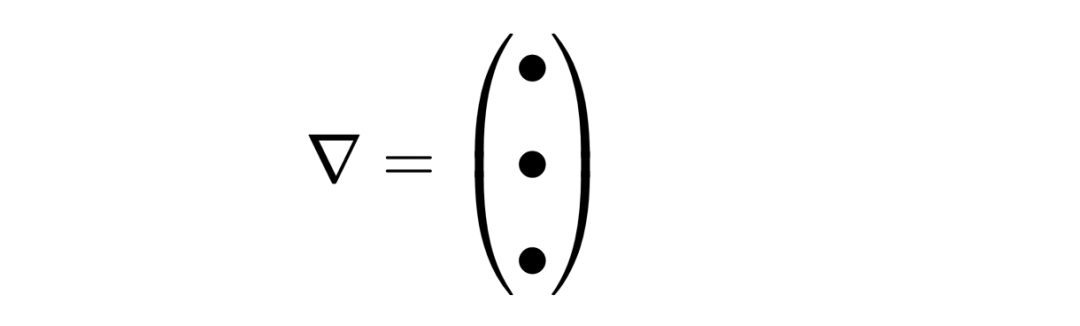
然而,它的組成部分不是數字,而是導數,對應于空間坐標。第一個組成部分是關于x的導數,第二個組成部分是關于y的導數,第三個組成部分是關于z的導數。
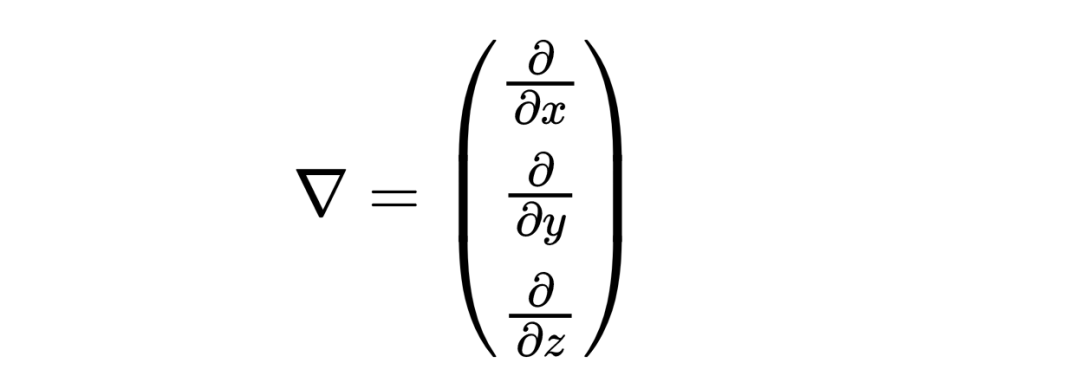
像nabla算子這樣的算子只在應用到一個場時起作用,
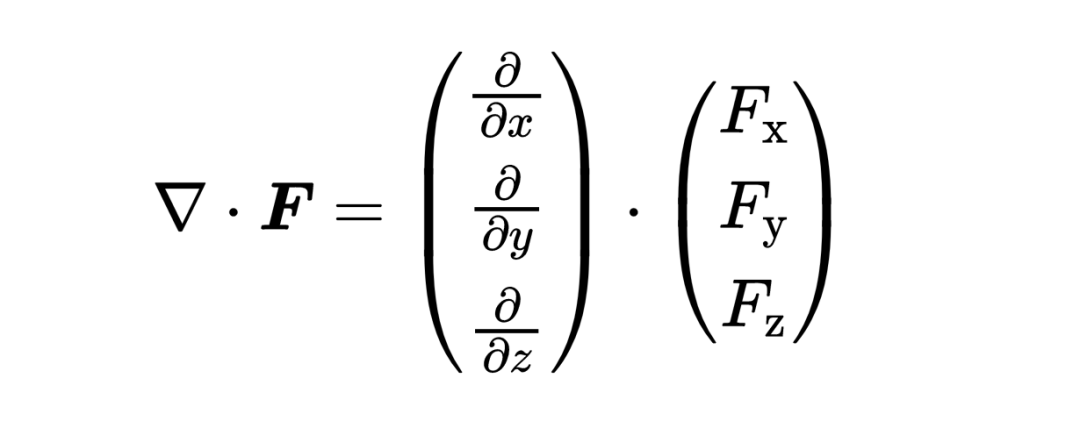
nabla算子應用到矢量場,通過在nabla算子和矢量場之間取標量積。你可以看到,這是矢量場對空間坐標x, y, z的導數的和,
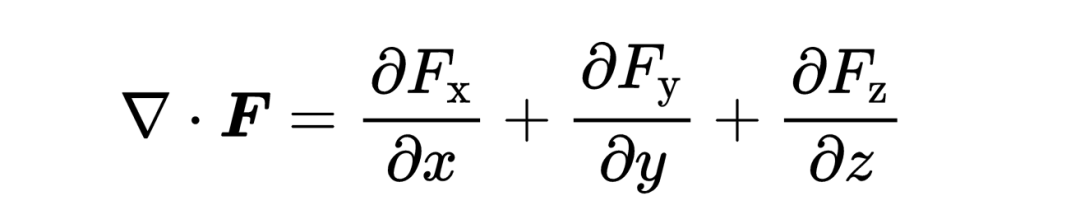
這樣一個nabla算子和矢量場F之間的標量積被稱為矢量場F的散度(Divergence ofF)。在位置x, y, z的結果不再是一個矢量,而是一個標量,它可以是正的,負的,或者是零。
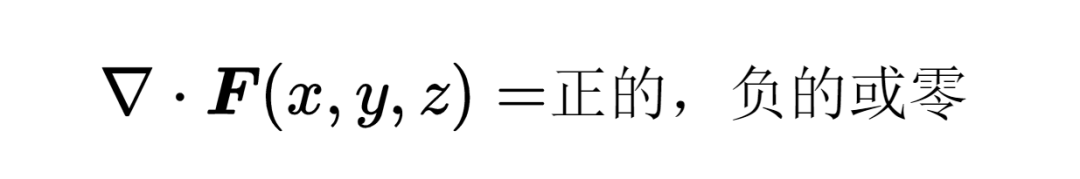
如果在位置x, y, z的散度是正的,那么在這個位置(下圖正方體中的圓點)有一個矢量場F的源。如果這個位置被表面包圍,那么通過表面的通量也是正的,矢量場可以說是從表面流出。
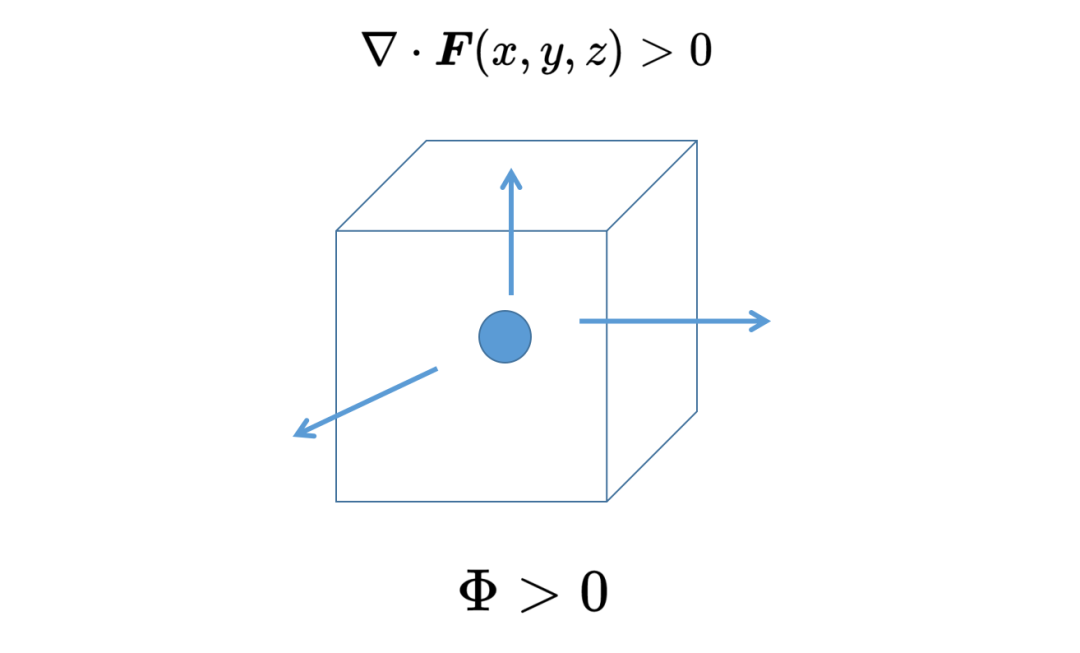
如果在位置x, y, z的散度是負的,那么在這個位置(下圖正方體中的圓點)有一個矢量場F的匯,如果這個位置被表面包圍,那么通過表面的通量也是負的,矢量場流入表面。
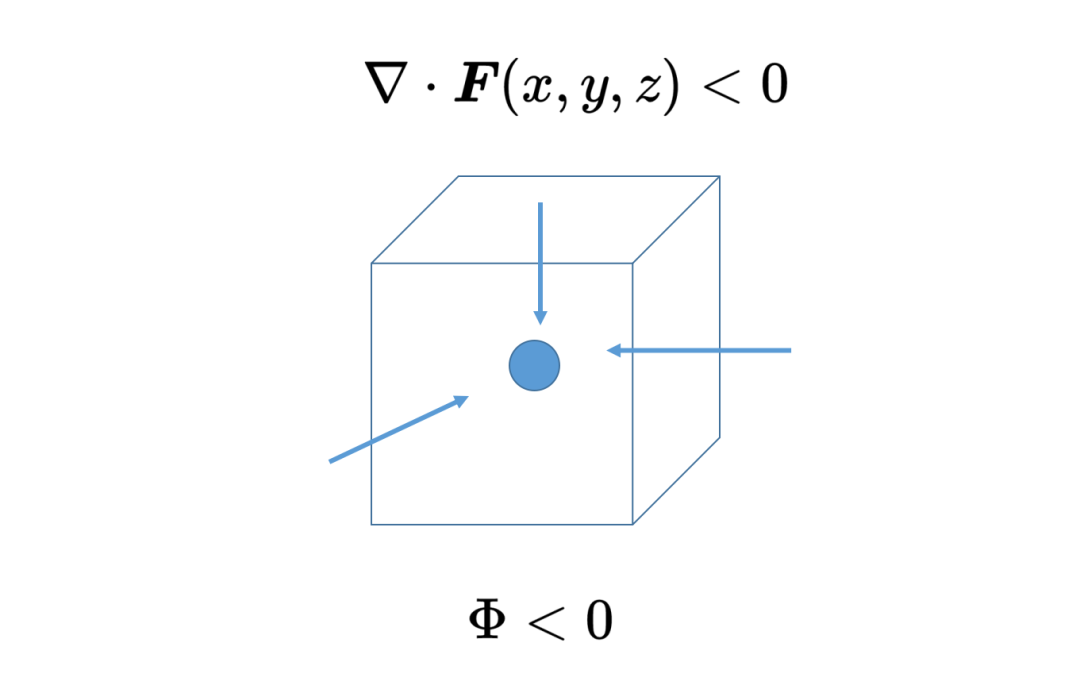
如果在位置x, y, z的散度消失,那么這個位置既不是矢量場的匯也不是源。矢量場不會流出或流入,或者說流入的和流出的數量相等,所以這兩個量抵消了。
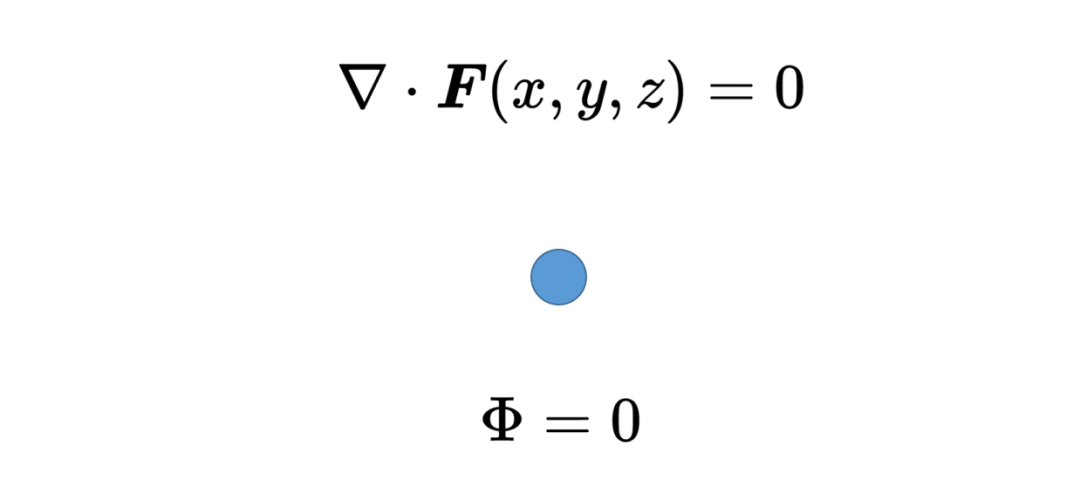
接下來,利用積分在體積內的每一個位置求和散度,即矢量場的源和匯。這種對體積小片段求和的積分被稱為體積積分。
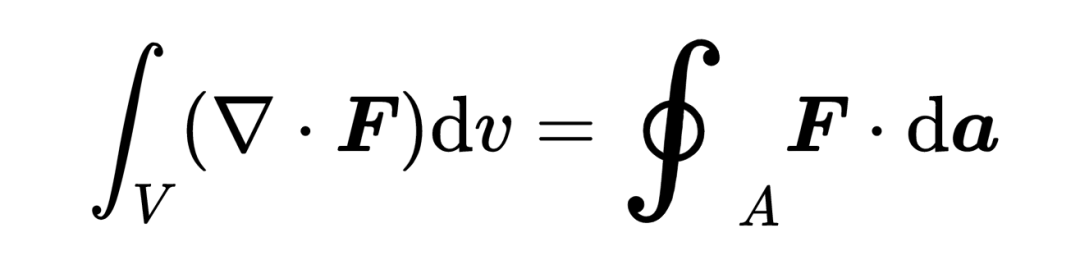
那么讓我們總結一下散度定理:在左邊是矢量場在體積內的源和匯的總和,而在右邊是矢量場通過那個體積的表面的總通量,這兩邊應該是相等的。散度定理因此表明,在一個體積內的矢量場的源和匯的總和,就是矢量場通過那個體積的表面的通量。
旋度定理
現在考慮理解麥克斯韋方程必要的第二個重要定理,旋度定理(斯托克斯定理),旋度積分定理:
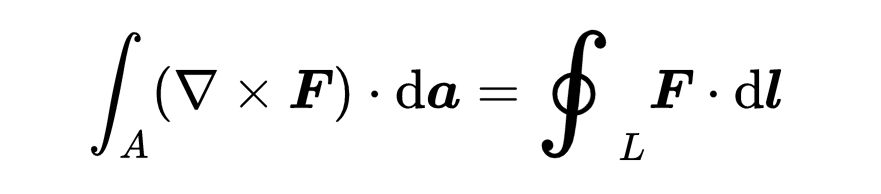
如果你理解了散度積分定理,那么旋度積分定理對你來說不應該很難。你已經知道矢量場F、標量積、Nabla運算符和da元素。首先,讓我們看看等式的右側。
L是空間中的一條線。積分符號上的圓圈表示這條線必須是閉合的,也就是說它應該形成一個循環。

dl是循環的一個無窮小線元素,所以是線的一個無限小的部分。再次,你應該注意到dl元素被顯示為粗體,它是一個具有大小和方向的矢量。現在形成了矢量場F和線元素dl的標量積。你已經知道標量積的任務是什么。首先,將矢量場分解為兩個部分;一個是平行于dl元素的'F平行',另一個是垂直于dl元素的'F垂直'。
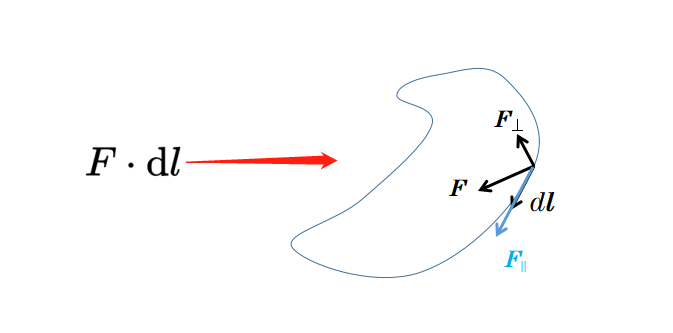
與dl元素的標量積消除了垂直分量,而沒有改變平行于dl元素的矢量場部分。因為在每個位置,dl元素都沿著線,所以在標量積中,只有沿著線L的矢量場部分被考慮;矢量場的其他部分被忽略。然后,使用積分對循環的每個位置的標量積進行求和。這樣的積分,其中無限小的線元素被求和,被稱為線積分。
現在你知道在旋度積分定理的右側的含義:線積分計算了多少的矢量場F沿著線L運動。
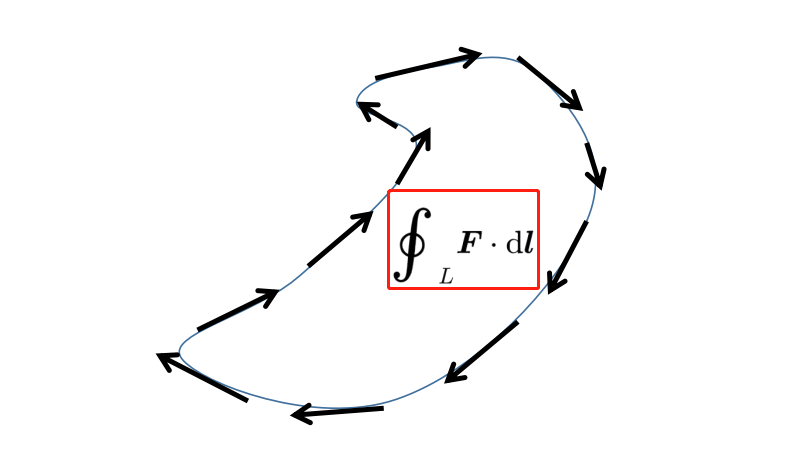
因為線是閉合的,這個標量積返回到求和開始的同一個點。閉合線積分因此表示矢量場F沿著環路L旋轉的程度。如果這個線積分中的矢量場F是一個電場E,那么這個線積分被稱為線路L上的電壓。
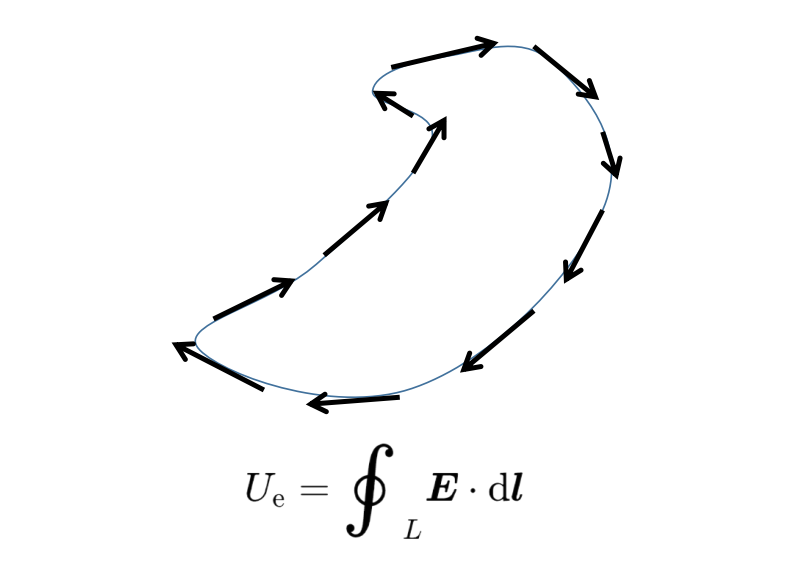
另一方面,當矢量場F是一個磁場B時,線積分被稱為線路L上的磁電壓。
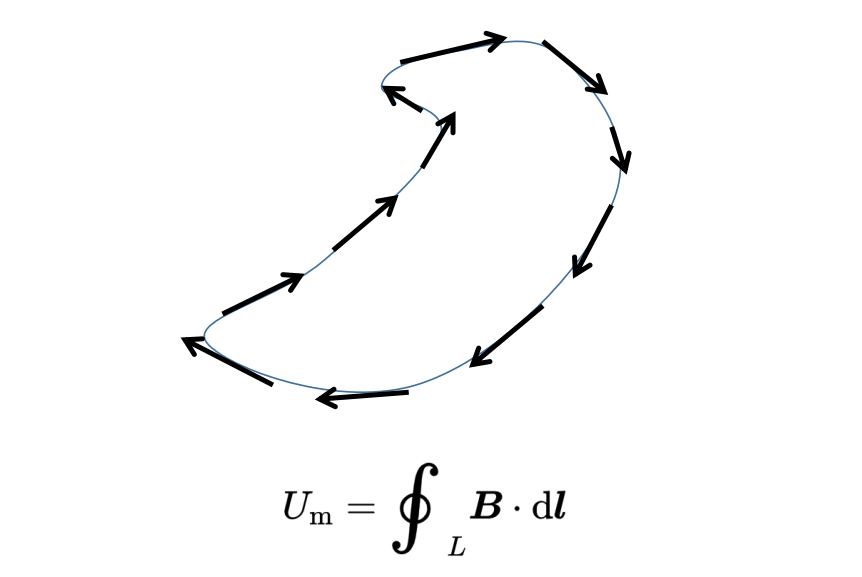
在電場的情況下,電壓與通過線路L的正電荷粒子獲得的能量成正比。
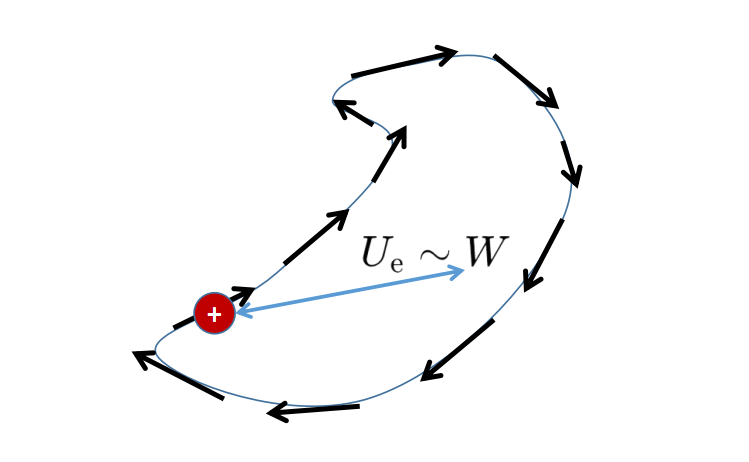
相反,負電荷粒子在通過線路L時會失去這種能量。電場的線積分,也就是電壓,衡量了在考慮的線路L通過下,帶電粒子的能量增益或能量損失。現在你應該已經理解了旋度積分定理的右側了。
讓我們現在看看左側。
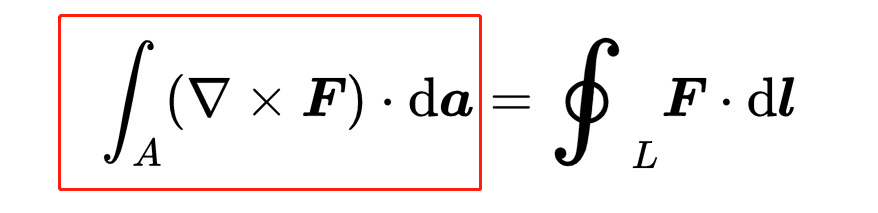
這里再次出現了面積A。這個面,不像散度積分定理,不必是一個封閉的面,而只是線L所包圍的面。da再次是面積A的一個無窮小部分,它在任何位置都垂直于該表面。
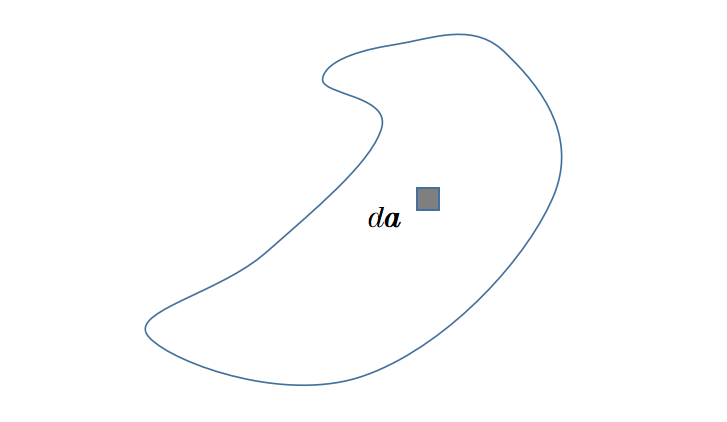
此外,這里出現了叉積,我們在討論磁力時已經遇到過它。這里,叉積是在Nabla運算符和矢量場F之間形成的。除了標量積,它是兩個矢量相乘的第二種方式。Nabla運算符和矢量場F之間的這個叉積被稱為矢量場F的旋度。
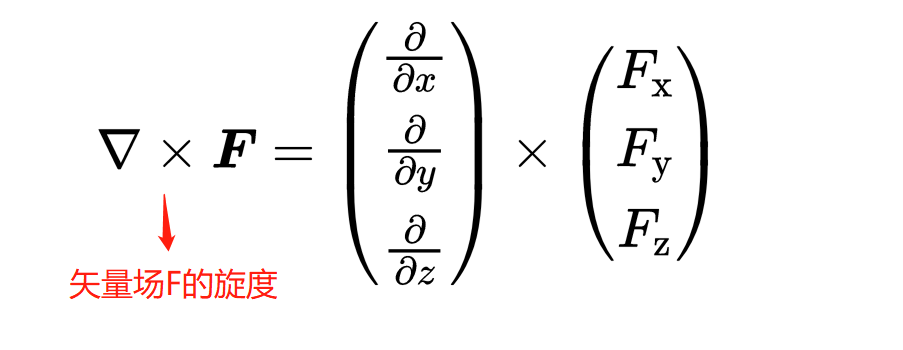
結果(與標量積相反)又是一個矢量場。
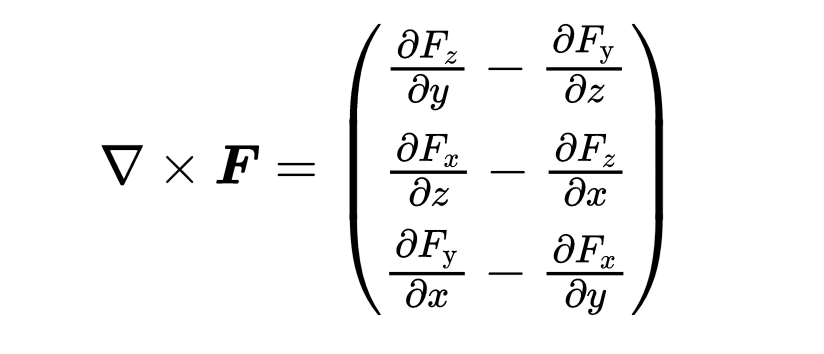
這個新的矢量說明了在表面A內一個點周圍,F場有多少旋轉。
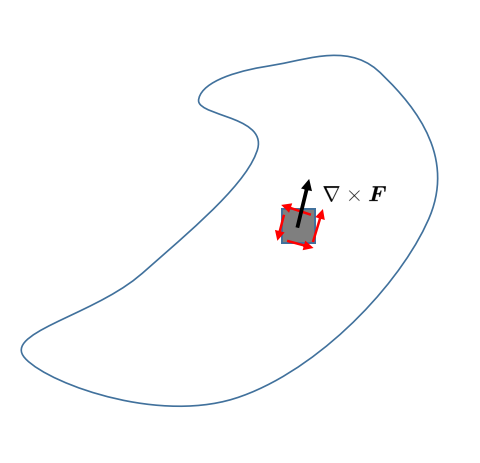
然后,新的矢量場'Nabla叉F'與無窮小表面元素da之間形成了標量積。因此,正如你已經知道的,只有'Nabla叉F'的一部分被留下,這部分平行于表面元素。
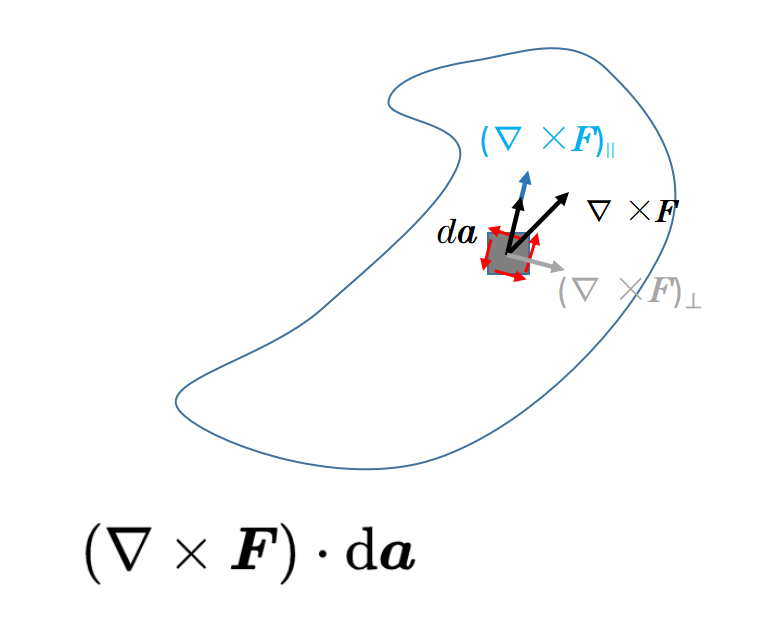
由于表面元素da垂直于表面A,標量積只保留矢量場'Nabla叉F'的一部分,這部分也是垂直于表面A。然后,通過積分,將表面A內的所有標量積分求和。
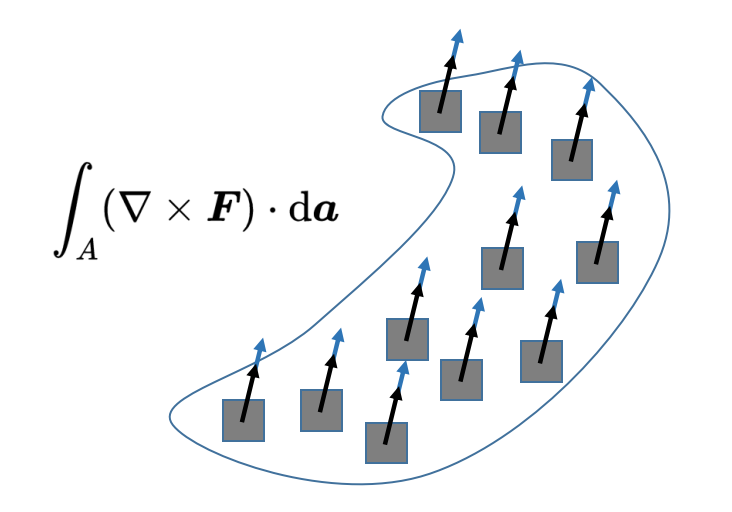
讓我們總結一下旋度積分定理的陳述:在右側,沿著一條線L加總矢量場F,因此,考慮了矢量場圍繞封閉表面的旋轉。在左側,對矢量場F的旋度在表面內的每一個獨立的點進行求和。根據這個定理,兩邊應該是相等的。旋度積分定理因此表明,矢量場F在表面A內的總旋度對應于矢量場F沿著該表面的邊緣L的旋轉。
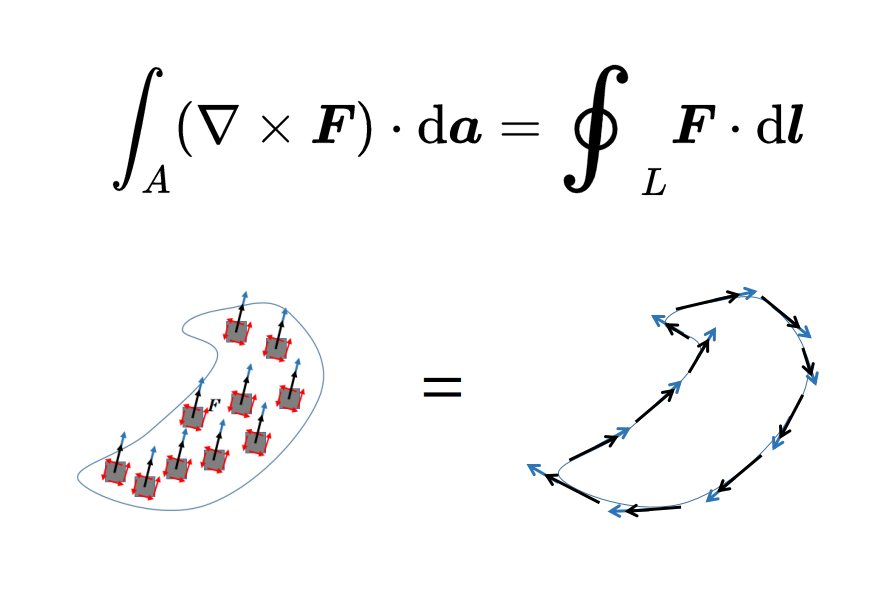
顯然,表面內部的矢量場的旋轉在求和過程中抵消了,只剩下沿著邊緣L的矢量場的旋轉。
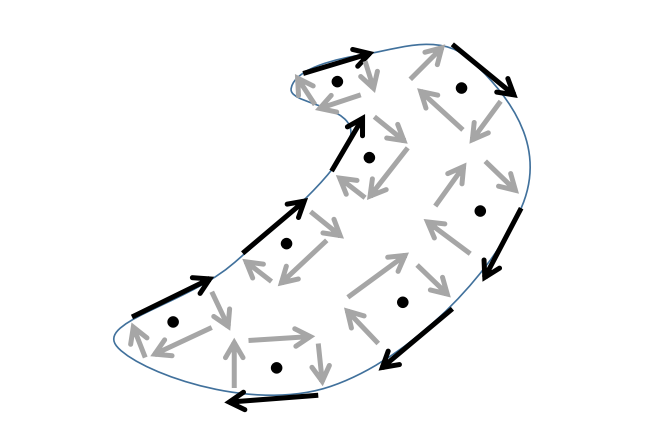
有了所有這些,你現在應該已經準備好完全理解麥克斯韋方程了。
第一個麥克斯韋方程
這就是積分形式的第一個麥克斯韋方程,
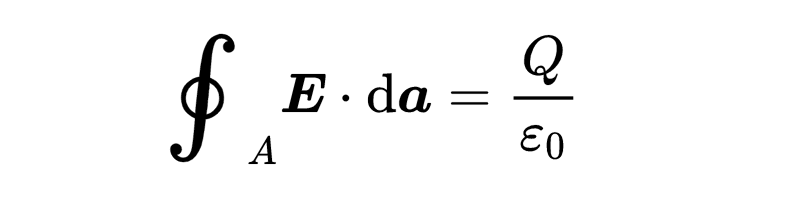
麥克斯韋方程的左側應該對你來說是熟悉的。這是一個表面積分,其中出現了電場E。這個積分計算有多少電場出入表面A。
因此,這個積分代表了通過表面A的電通量。
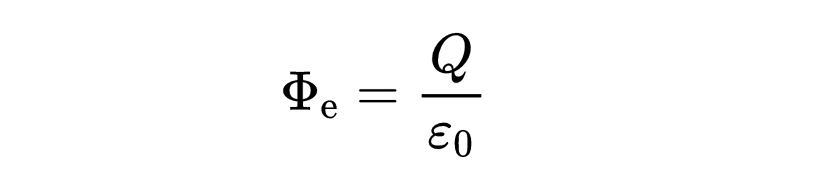
右側是被表面A包圍的總電荷Q,除以電場常數(以得到正確的單位)。
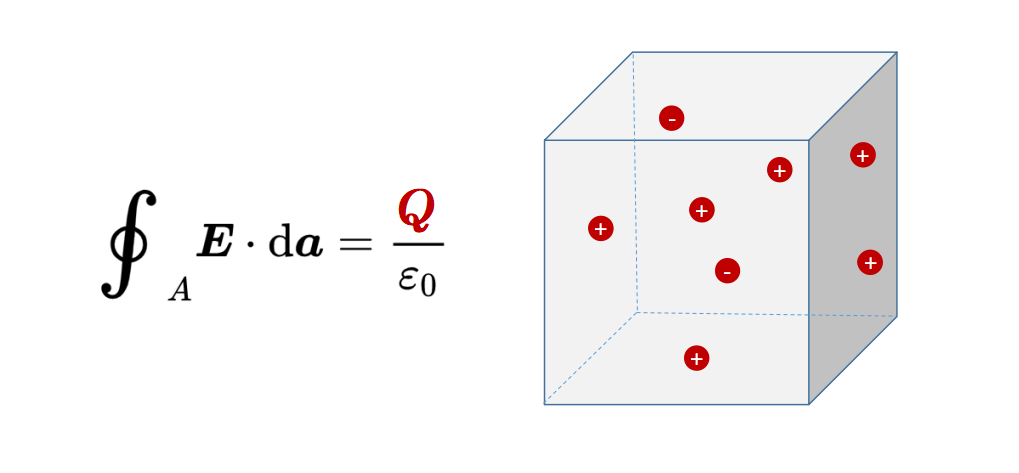
第一個麥克斯韋方程表明,通過封閉表面A的電通量Phi對應于被這個表面包圍的電荷Q。
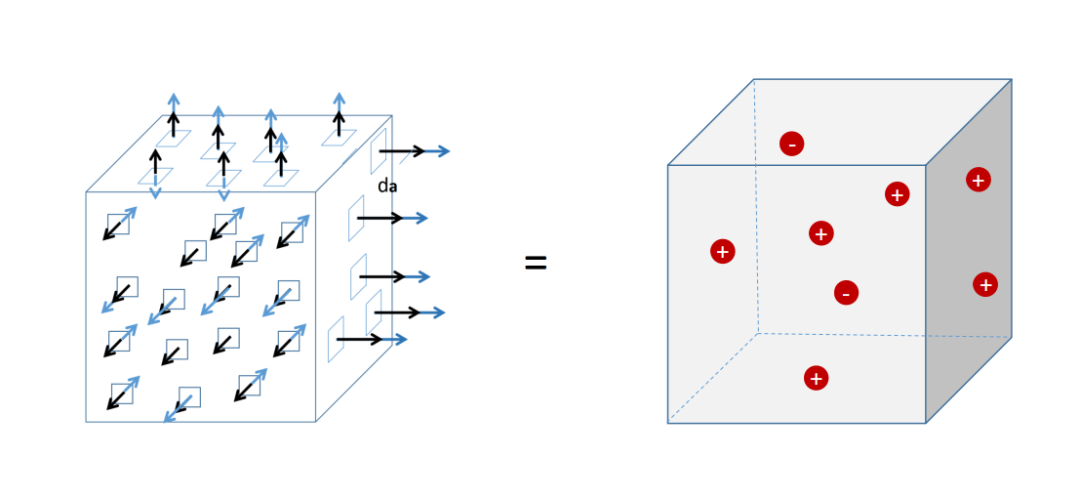
順便說一句:庫侖定律是第一個麥克斯韋方程的一個特例。
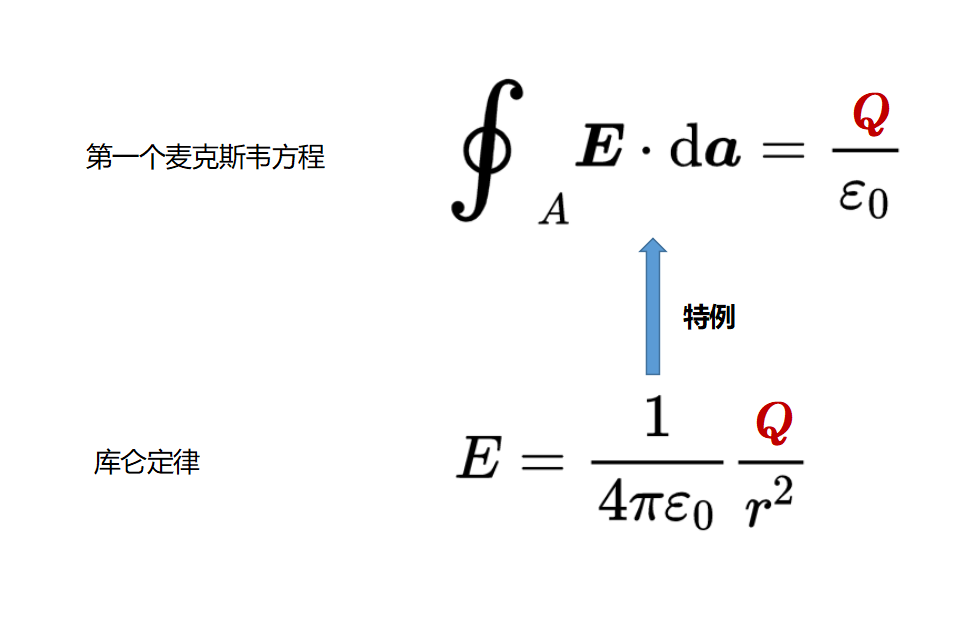
利用之前學習的散度積分定理,它結合了體積積分和表面積分:
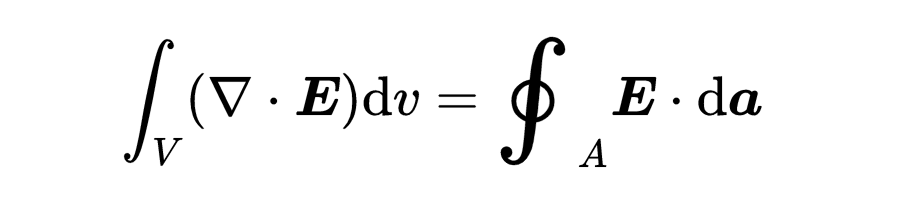
第一個麥克斯韋方程左側的表面積分可以被替換為電場散度的體積積分,
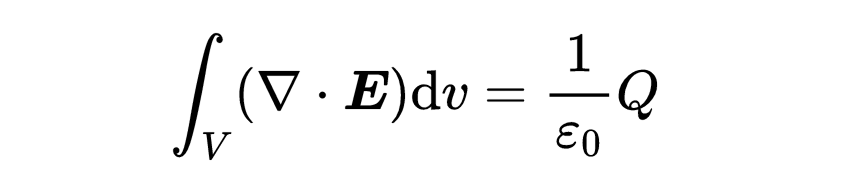
封閉的電荷Q也可以用體積積分來表示。根據定義,電荷密度是電荷除以體積。將體積移到另一側,那么就有了'Q等于rho乘以V'。體積V通常可以寫成體積積分的形式。

也就是說,電荷密度rho對體積V的體積積分是封閉在該體積內的電荷。這使得麥克斯韋方程的右側變成了一個體積積分。
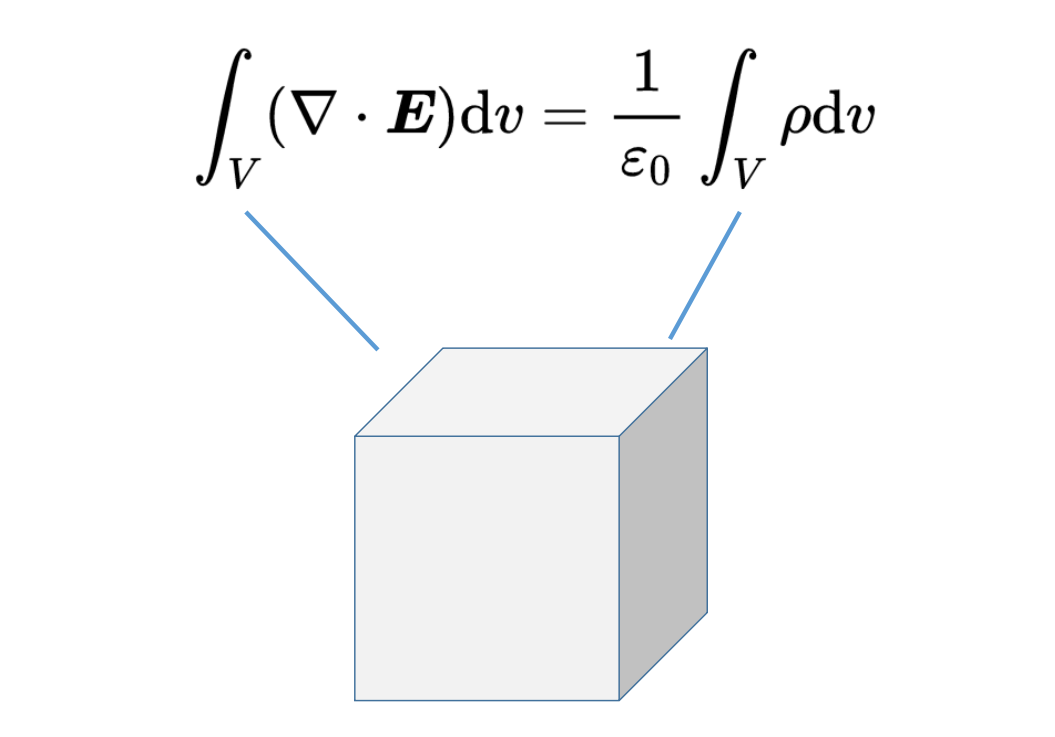
如你所見,我們在兩邊都對同一個體積V進行了積分。為了滿足這個方程對于任意選擇的體積V,兩邊的被積函數必須相等。現在你已經發現了第一個麥克斯韋方程的微分形式:
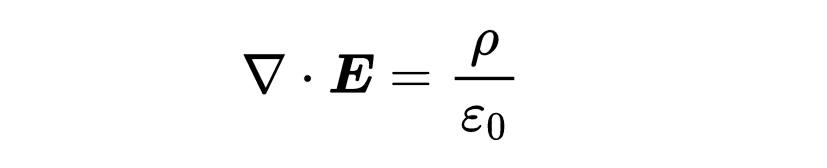
在微分形式的左側,你可以看到電場的散度。你知道在空間的一個特定點上,它可能是正的、負的或者零。
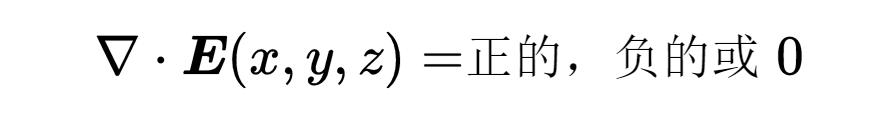
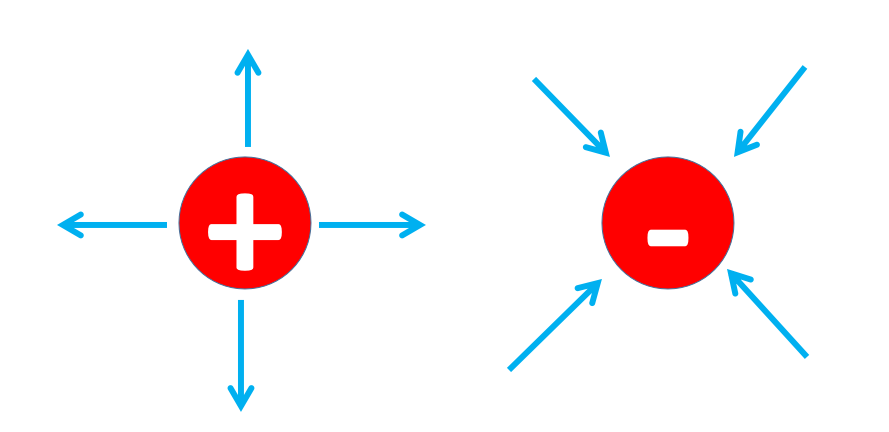
散度的符號決定了在考慮的空間點上的電荷的類型。如果散度是正的,那么在這個空間點上的電荷密度rho就是正的,因此電荷也是正的。因此,在這個空間點有一個正電荷,這是電場的來源。如果散度是負的,那么電荷密度rho就是負的,因此電荷也是負的。在這個空間點上,因此有一個負電荷,這是電場的匯流點。
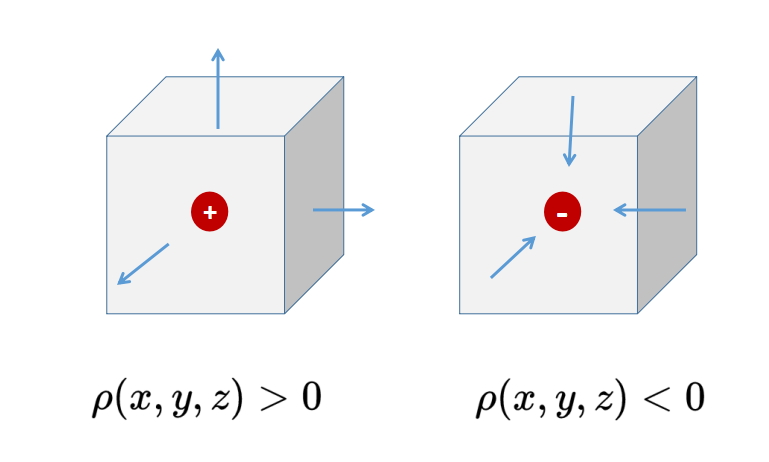
如果散度為零,那么電荷密度rho也為零。在空間的這個點,要么沒有電荷,要么正電荷和負電荷的數量一樣多,因此這個點的總電荷被抵消了。
第一個麥克斯韋方程(微分形式)聲明電荷是電場的源和匯。電荷生成電場!
第二個麥克斯韋方程
這是第二個麥克斯韋方程的積分形式,
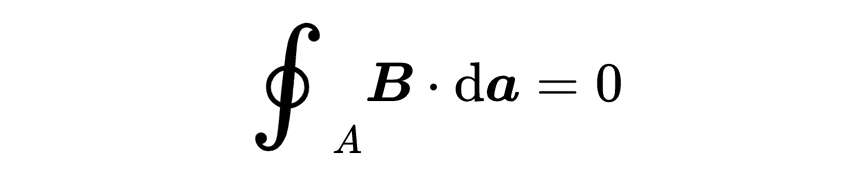
這個方程沒有什么陌生的內容。所有的東西現在應該看起來都很熟悉。在等式左側,你看到了一個關于A的面積積分。這次不是電場的積分,而是磁場B的積分。根據等式,通過封閉表面A的磁通量總是等于零。
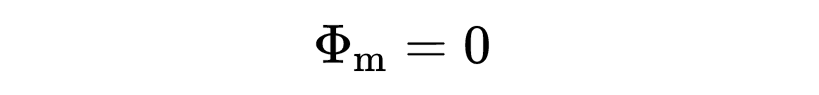
第二個麥克斯韋方程表明,總是有和進入表面的磁場矢量一樣多的磁場矢量從表面出來。
通過散度積分定理,面積積分可以轉換為體積積分;這樣,磁場的散度就起到作用了。這個積分應該是零。對于任何體積V的積分,只有在被積函數為零的情況下才總是零。
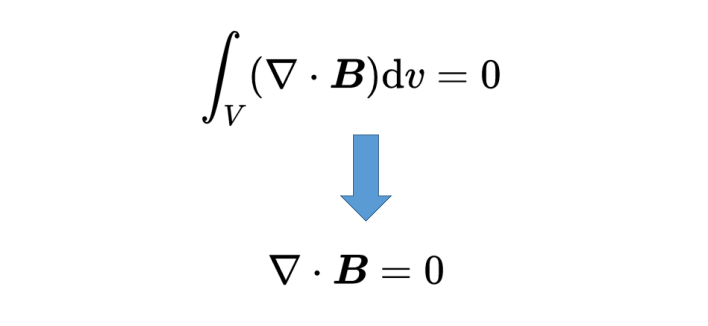
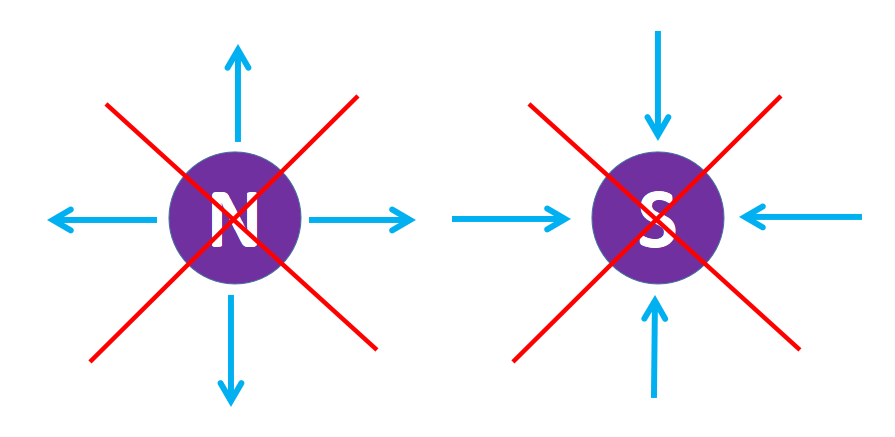
因此,第二個麥克斯韋方程以其微分形式出現:“B的散度等于零”。如果散度為零,這意味著在空間的每一個點(x, y, z)上,要么沒有磁電荷(也稱為磁單極子),要么正磁電荷和負磁電荷的數量一樣多,所以那一點的總電荷抵消了,就像一個理想的磁偶極子,它總是有一個北極和一個南極。
北極對應正磁電荷,南極對應負磁電荷。由于沒有磁單極子,所以沒有分離的磁場源和匯。第二個麥克斯韋方程的微分形式表明,沒有磁單極子產生磁場。只有磁偶極子可以存在。
第二個麥克斯韋方程,就像其他麥克斯韋方程一樣,是一個實驗結果。也就是說,如果有一天發現了一個磁電荷,那么第二個麥克斯韋方程就必須被修改。然后麥克斯韋方程將看起來更加對稱,更加美麗!
第三個麥克斯韋方程(法拉第感應定律)
這是第三個麥克斯韋方程在積分形式下的樣子,
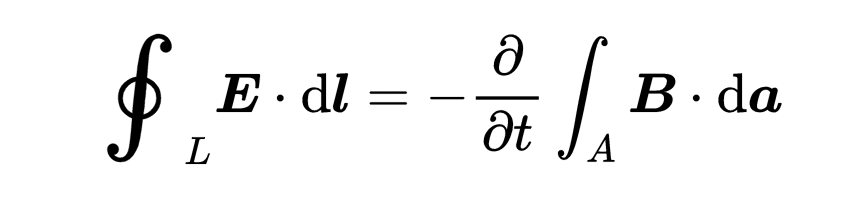
你可能已經知道第三個麥克斯韋方程,也就是法拉第的感應定律。這就是感應定律的最一般形式。
左側是電場E沿一個封閉線L的線積分,它形成表面A。這個積分把沿著線L運動的電場的所有部分都加起來。這個積分對應于沿著線L的電壓U。
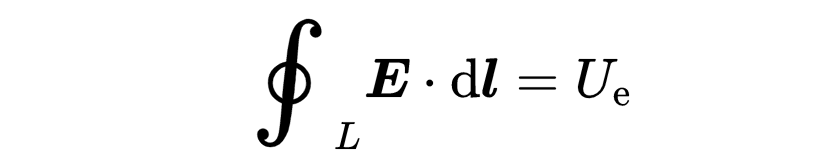
在右側有一個關于任意表面A的磁場B的面積積分。這個積分對應于通過表面A的磁通量Φ。這個磁通量是相對于時間t進行微分的。
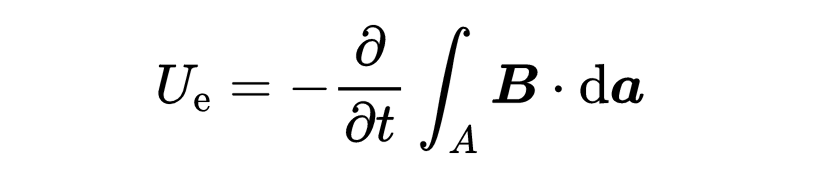
磁通量的時間導數表示隨著時間的流逝磁通量變化了多少。所以它是磁通量的時間變化。
磁通量的變化越大,旋轉電場就越大。
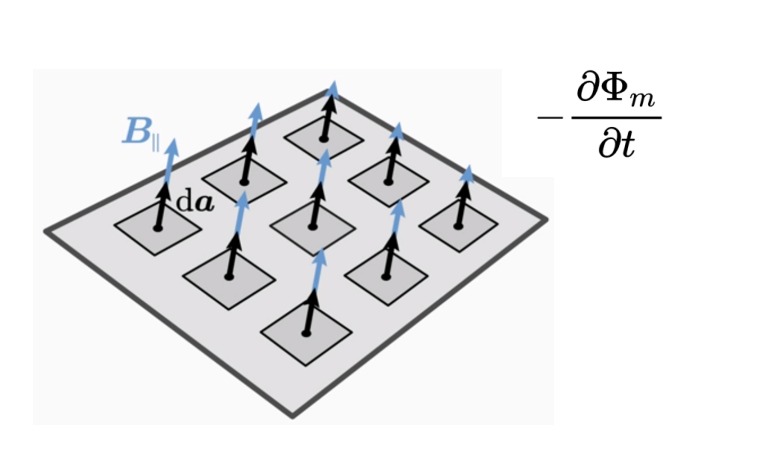
負號考慮了旋轉的方向。如果磁通量的變化是正的,電壓就是負的。如果磁通量的變化是負的,電壓就是正的。電壓和磁通量的變化在行為上是相反的。負號保證了能量守恒。也許你知道這個名字:楞次定律(lenz's law)。
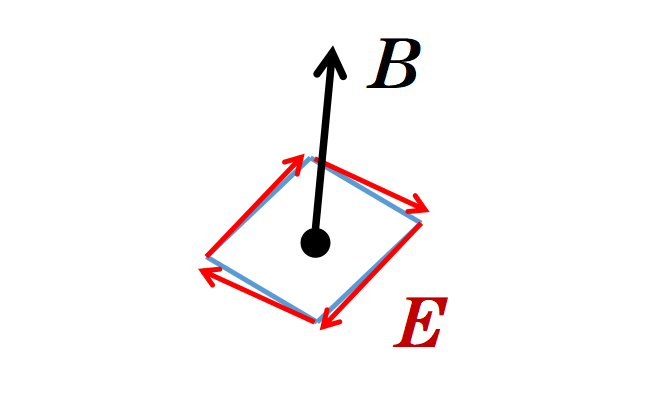
正如你所看到的,根據這個麥克斯韋方程,旋轉電場產生了隨時間變化的磁場,反之亦然。
所以讓我們總結一下:第三個麥克斯韋方程表明,沿著一個封閉線的電壓對應于通過該線邊界的表面的磁通量的變化。換句話說,通過表面A的磁通量的變化會在A的邊緣產生電壓。
讓我們考慮另一個重要的特殊情況。如果磁場不隨時間變化,那么麥克斯韋方程的右側就會被消除。
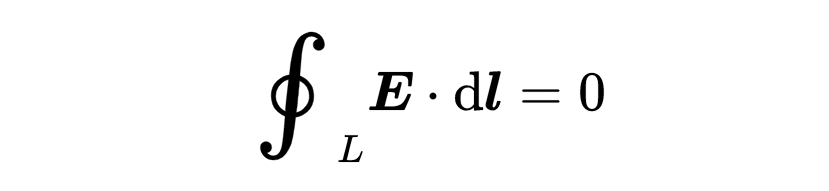
然后這個方程就表明,沿著一個封閉線的電壓總是零。所以只有當磁場不隨時間變化時,才沒有旋轉電場。
如果一個電子通過封閉線L,它的能量不會改變,因為,電壓表示一個電荷在通過一條線時獲得或失去的能量。在這種情況下,電壓為零。因此沒有能量變化。
使用旋度積分定理,可以將積分形式轉化為微分形式。這個定理將線積分與面積積分相連。為此,只需將線積分替換為面積積分。這就引出了E的旋度。
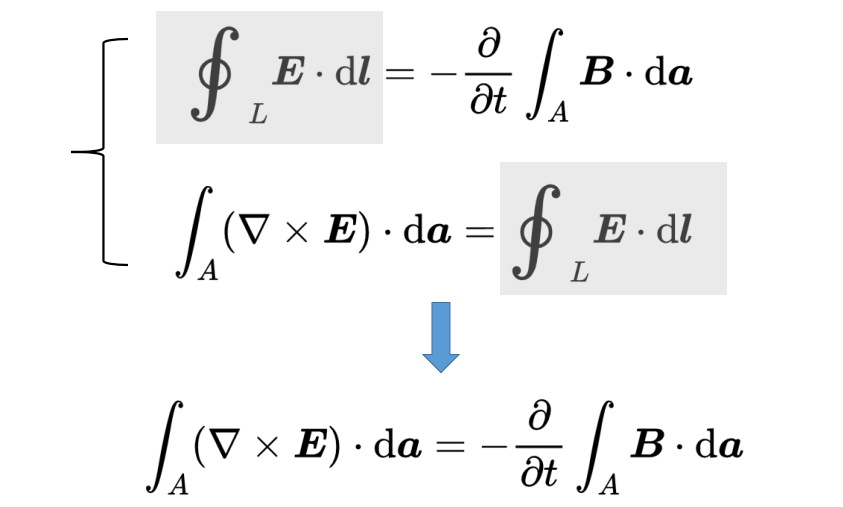
在另一邊,你可以把時間導數放進積分里,
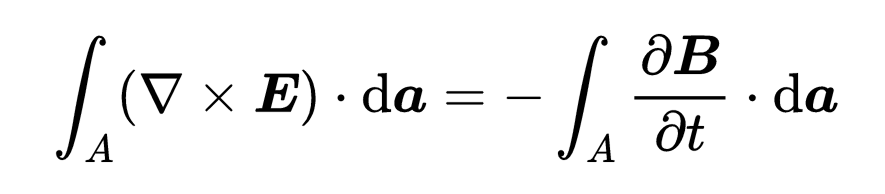
由于方程對任何表面A都適用,所以兩邊的被積函數必須相等。就這樣,你發現了第三個麥克斯韋方程的微分形式:“E的旋度等于磁場的負時間導數”,
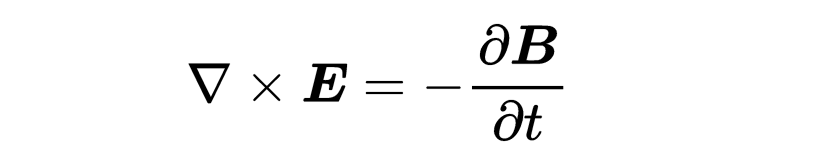
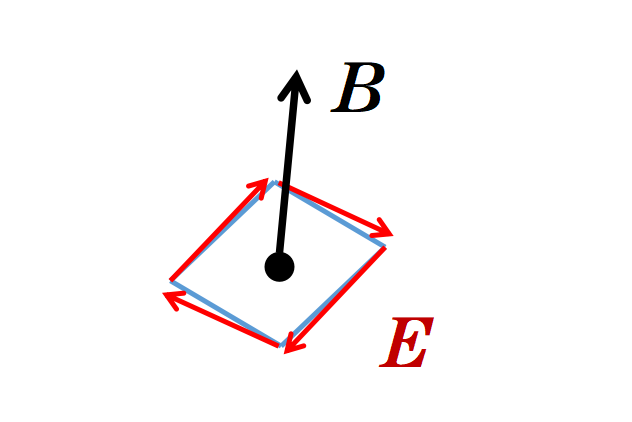
微分形式的第三個麥克斯韋方程表明,一個變化的磁場B會產生一個旋轉的電場E,反之亦然,以保證能量守恒。
我們現在轉向第四個,也是最后一個麥克斯韋方程。
第四個麥克斯韋方程
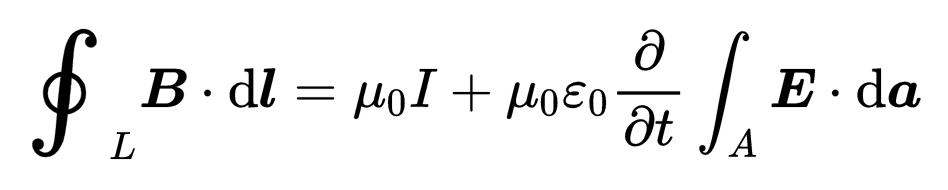
左側的積分是什么類型的?沿封閉線L的磁場B的線積分,這就是磁電壓U的定義,
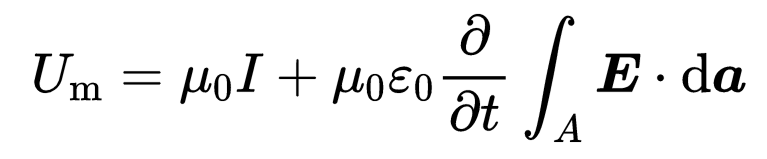
右側有電場常數Epsilon_0和磁場常數Mu_0。它們確保了麥克斯韋方程兩側的單位是一樣的:
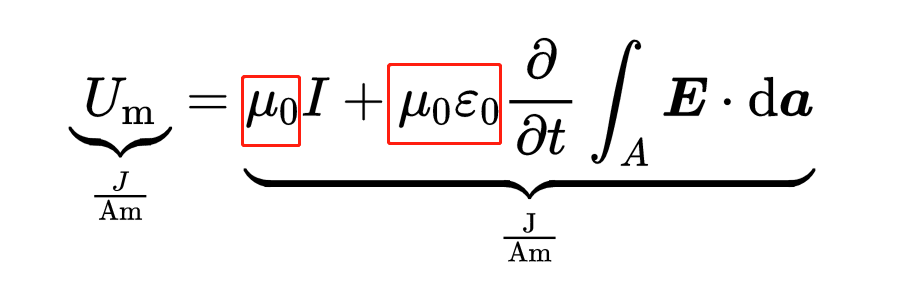
此外,這里還有一些新的東西,那就是電流I。當電荷沿導體流動時,它們會產生一個電流I。此外還有另一個加數:
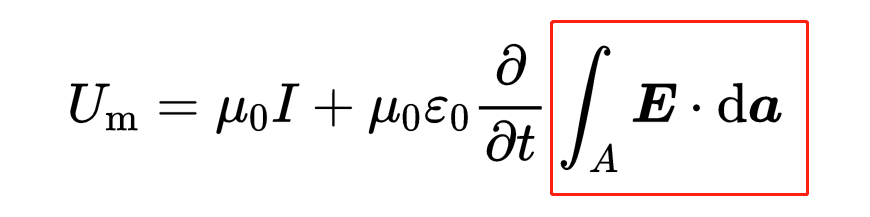
我們知道電場的面積積分,就是通過表面A的電通量。此外,電通量前面還有一個時間導數。所以整個式子就是電通量的時間變化。
總結一下:右側有兩個加數:一個由電流貢獻,一個由電通量的變化貢獻。
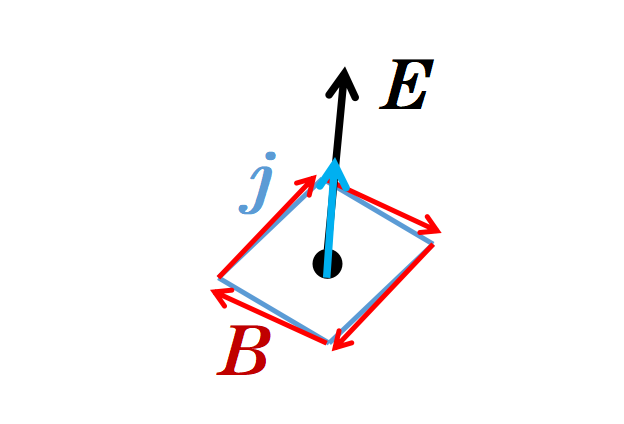
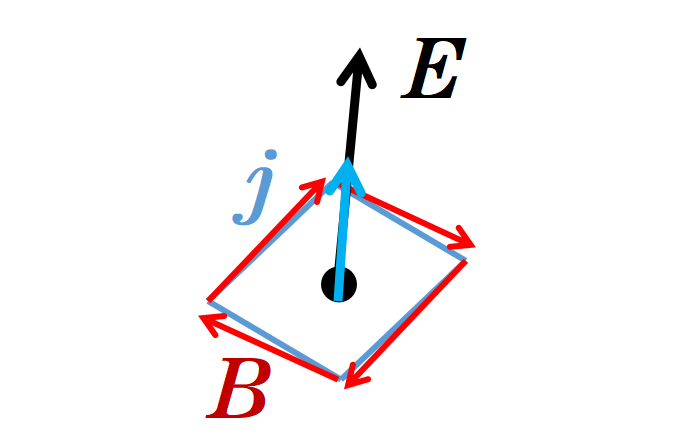
因此,第四個麥克斯韋方程表明,旋轉磁場首先由穿過面積A的電流產生,其次由變化的電場產生。
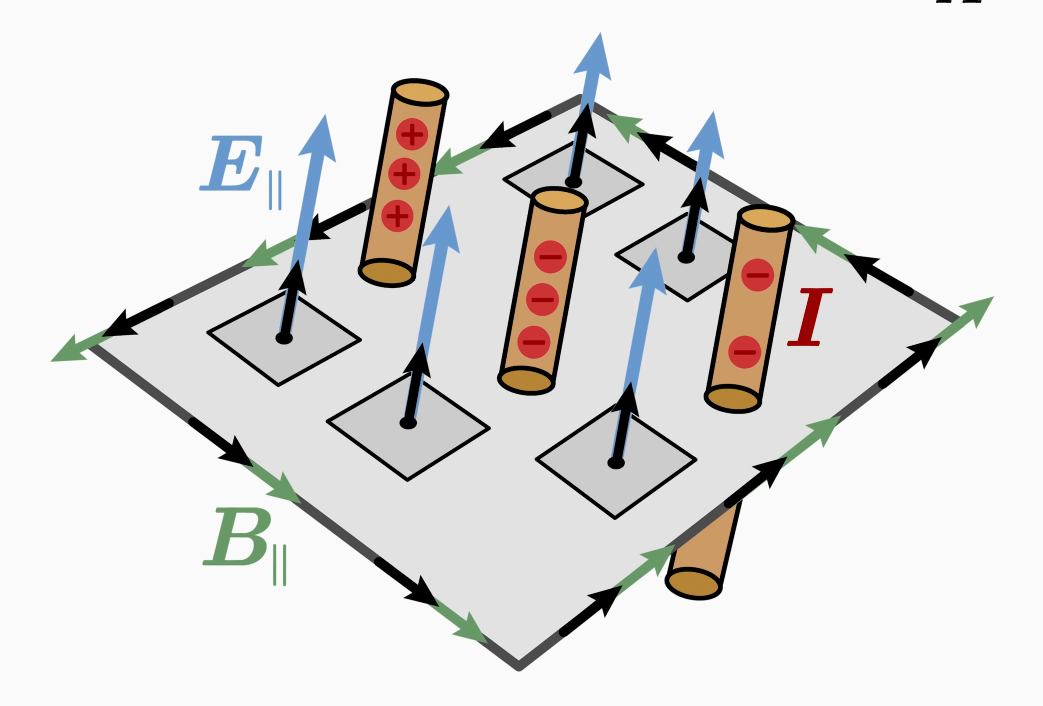
讓我們現在推導出微分形式。利用旋度積分定理,可以將線積分轉化為面積積分,從而引入磁場B的旋度。
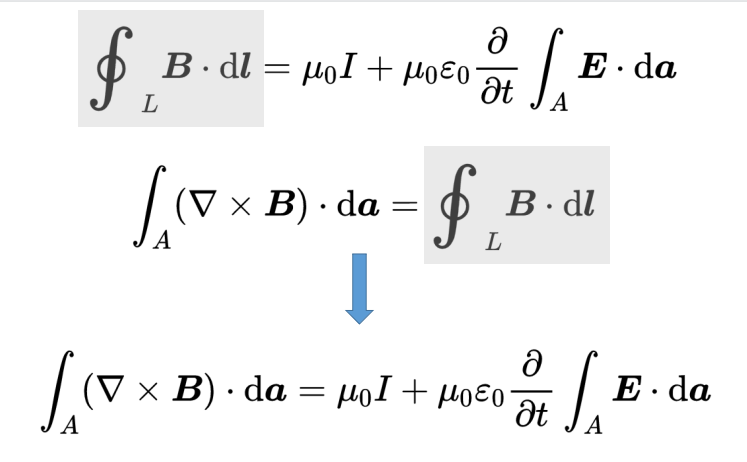
現在我們需要用面積積分來表示電流I,這樣我們在右邊就能得到一個單一的被積函數。我們可以簡單地使用電流密度j來做到這一點,
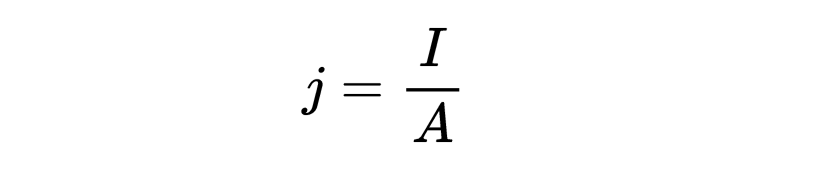
它表示電流流過的區域的電流。因此,電流也可以寫成電流密度j在表面A上的面積積分,
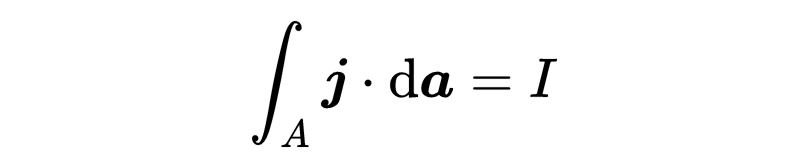
注意在積分中,電流密度與da元素的標量積被取出。所以我們只選取了電流密度矢量與da元素平行的部分。只有電流密度的這個平行部分才對通過面A的電流有貢獻。你可以將時間導數放進積分中,
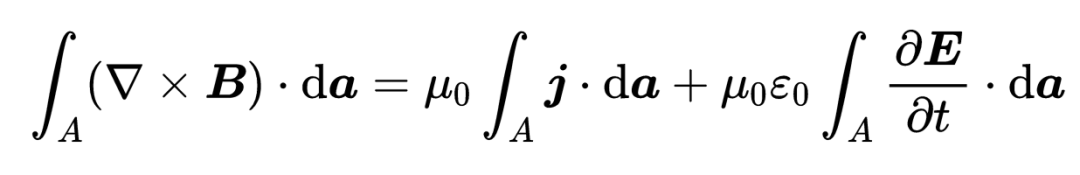
現在,由于在同一個表面A上積分,所以可以將兩個面積積分合并為一個,
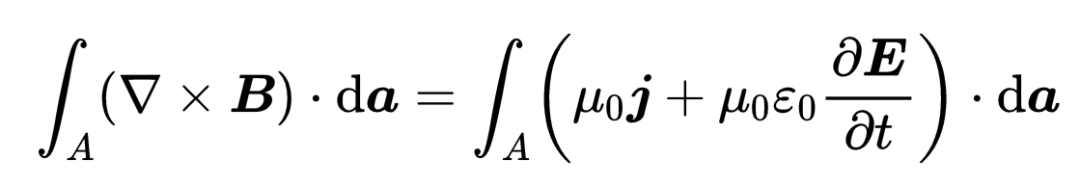
為了滿足對任何表面A的方程,兩邊的被積函數必須相等。我們已經找到了第四個麥克斯韋方程的微分形式:“B的旋度等于mu_zero乘以I + mu_zero epsilon_zero乘以電場隨時間的變化”:
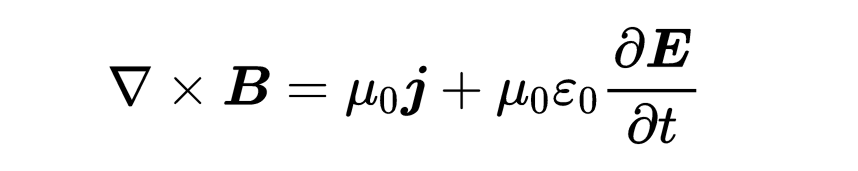
微分形式因此表明,在空間中的一個點處,磁場B的旋度有兩種原因:電流密度j和在這個點處變化的電場。
總結
讓我們以緊湊的形式(微分形式),總結電動力學的四個麥克斯韋方程。
第一個麥克斯韋方程:E的散度等于電荷密度除以epsilon_zero。電荷產生電場。
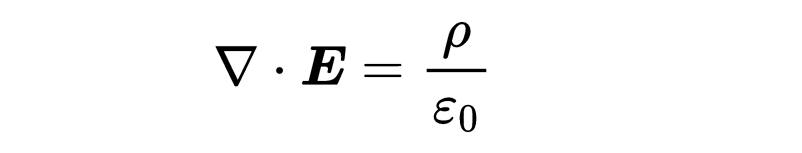
第二個麥克斯韋方程:B的散度等于零。沒有磁單極子。
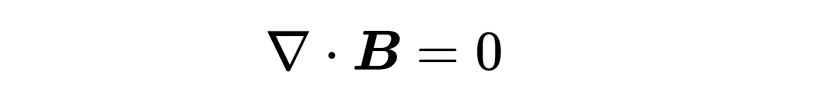
第三個麥克斯韋方程:E的旋度等于磁場的負時間導數。一個變化的磁場創造一個旋轉的電場,反之亦然。
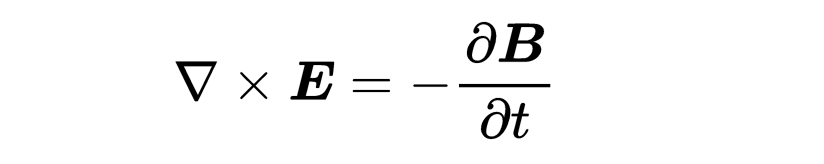
第四個麥克斯韋方程:B的旋度等于mu_zero乘以I + mu_zero epsilon_zero乘以電場隨時間的變化。電流和變化的電場生成磁場。
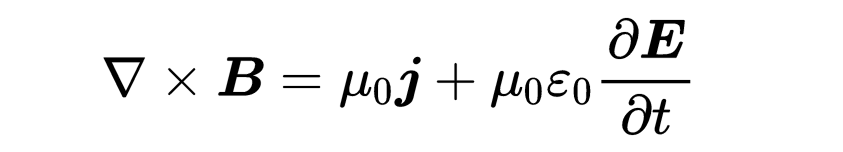
-
電動汽車
+關注
關注
156文章
12188瀏覽量
232464 -
磁場
+關注
關注
3文章
892瀏覽量
24318 -
WIFI
+關注
關注
81文章
5309瀏覽量
204799 -
無線電
+關注
關注
60文章
2149瀏覽量
116815 -
麥克斯韋
+關注
關注
0文章
19瀏覽量
5752
原文標題:深度解析麥克斯韋方程
文章出處:【微信號:mcu168,微信公眾號:硬件攻城獅】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
麥克斯韋方程組究竟帶來了什么
麥克斯韋Maxwell方程組是怎么來的
電磁場理論之麥克斯韋方程組論文的詳細資料免費下載
追逐麥克斯韋方程組與電磁波理論
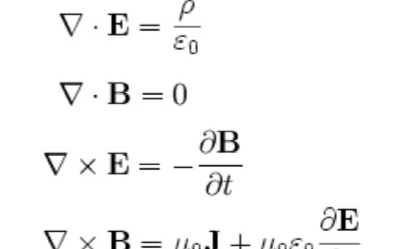
麥克斯韋方程組的詳細資料說明





 深度解析麥克斯韋方程
深度解析麥克斯韋方程
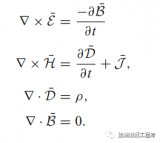










評論