文章來源：力學科普

原文作者：Lee

提到傅里葉變換，你是不是又想起了大學課程里被它支配的恐懼。其實，傅里葉分析不僅僅是一個數學工具，更是一種可以徹底顛覆一個人以前世界觀的思維模式。如果用方程寫一部科學史，傅里葉變換必然擁有位置，它的應用之廣，可以處理圖片，也可以解讀星空，可以幫忙建造不易倒塌的房子，也可以深度參與金融數據分析。無論是混雜的信號，還是復雜的卷積，都可以被它的魔法馴服，變得清晰明了、簡潔高效。那么，傅里葉變換是如何做到對萬物進行拆解的呢？

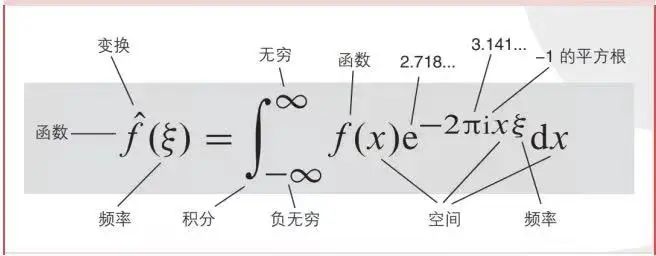
傅里葉變換最精彩之處就是能夠將信號在時域與頻域之間進行變換，因此我們先解釋一下什么是時域和頻域。所謂時域是描述數學函數或物理信號對時間的關系，從我們出生，我們看到的世界都以時間貫穿，股票的走勢、人的身高、汽車的軌跡都會隨著時間發生改變。這種以時間作為參照來觀察動態世界的方法我們稱其為時域分析。而頻域則描述了信號的頻率結構及頻率與該頻率信號幅度的關系，從這個視角來觀察世界你會發現世界是永恒不變的。這就好比在時域視角下我們觀察到鋼琴的琴弦一會上一會下的擺動，就如同一支股票的走勢；而在頻域視角則是永恒的音符。

簡單來說，傅里葉級數貫穿了時域與頻域，將任何形式的周期性信號無限拆解，分為多個有規律的簡單正弦波信號。而對于任何非周期性信號則可以看做是超大號的周期信號，作為傅里葉級數的延展，傅里葉變換可以將任何復雜的的非周期性信號規律性拆解。這就好比當我們去買菜的時候，各種蔬菜都不一樣，但都能轉換成“n個1斤砝碼+m個1兩砝碼”的組合。

從現代數學的眼光來看，傅里葉變換是一種特殊的積分變換。它能將滿足一定條件的某個函數表示成正弦基函數的線性組合或者積分。在不同的研究領域，傅里葉變換具有多種不同的變體形式，如連續傅里葉變換和離散傅里葉變換。

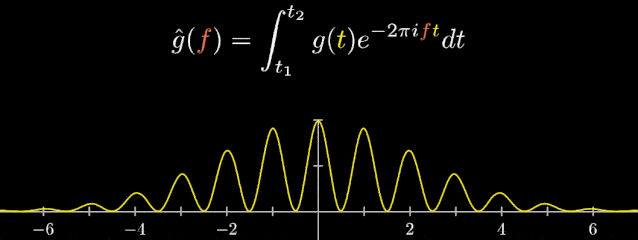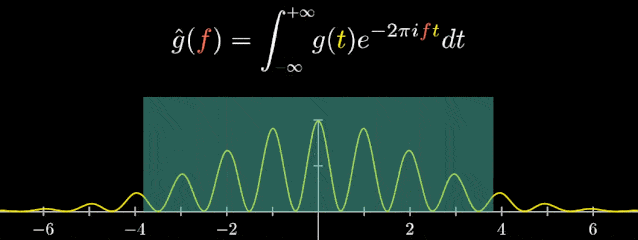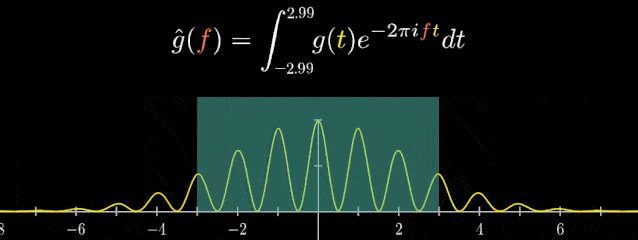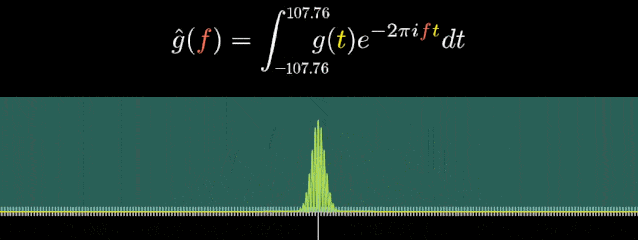
“傅里葉變換”最初被運用于熱力學分析中，隨著時代與科技的發展，它們也以各種方式被廣泛應用于醫學、聲學、密碼學、概率論、海洋學、計算機科學、量子力學等各個領域，下面舉一些傅里葉變換應用的實例。

岡薩雷斯在《數字圖像處理》一書中，將傅里葉變換比作一個玻璃棱鏡。棱鏡可以將光分解為不同顏色，顏色由波長（或頻率）來決定。傅里葉變換可以看作是數學上的棱鏡，將函數基于頻率分解為不同的成分。我們日常用美顏相機進行磨皮、美化操作的基本原理便是通過傅里葉變換，經過一定的處理，減少或增添某些頻率的幅度，達到讓圖像變得更模糊或更鮮亮的目的。

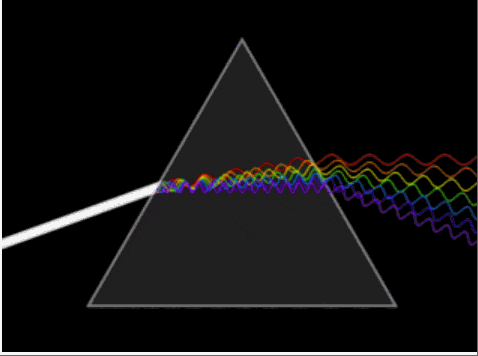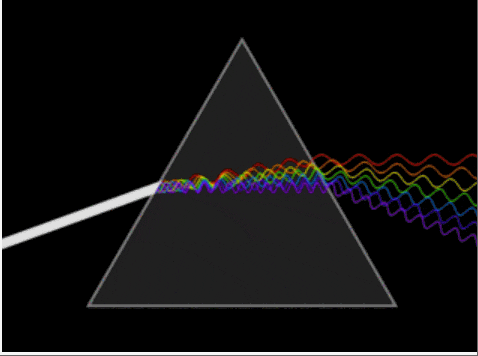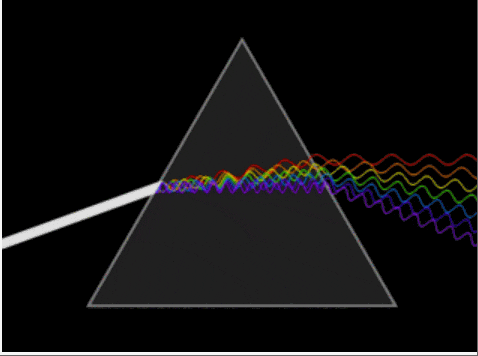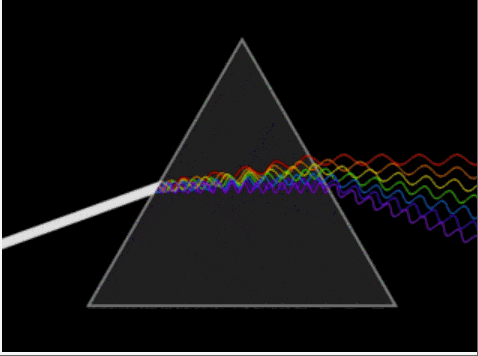
其實人類大腦本身就具有“傅里葉變換”的功能。例如，我們可以從一段嘈雜的公園環境音里分辨出男聲、女聲、老人、兒童、狗叫聲、腳步聲、水流聲和噪聲，下面這張圖形象地展示了這一過程，左邊的是你聽到的聲音，而右邊的圖則是你的大腦經過傅里葉變換，分析出了十幾種不同的發聲物體。市面上的變聲軟件，大叔嗓秒變蘿莉音的基本原理也是這樣，把一段音頻，分離出男聲和女聲，將男聲改為女聲的頻率，然后還原回去，實現男聲變女聲。

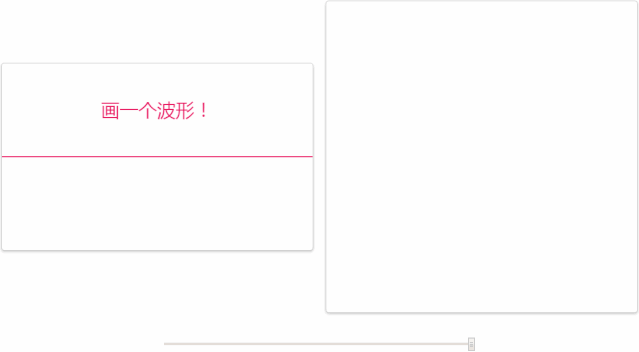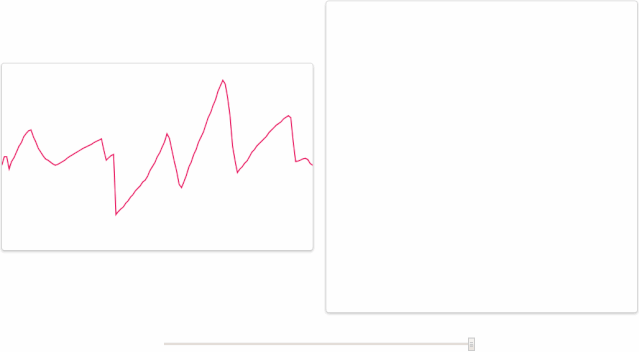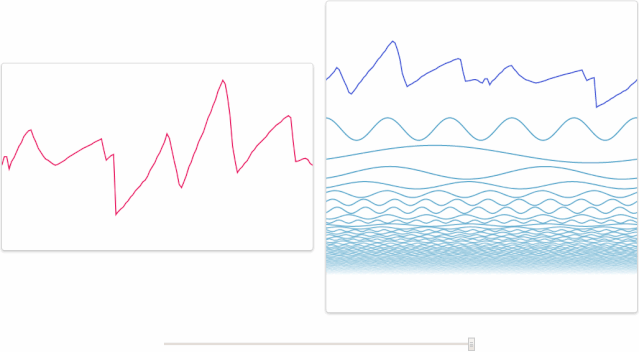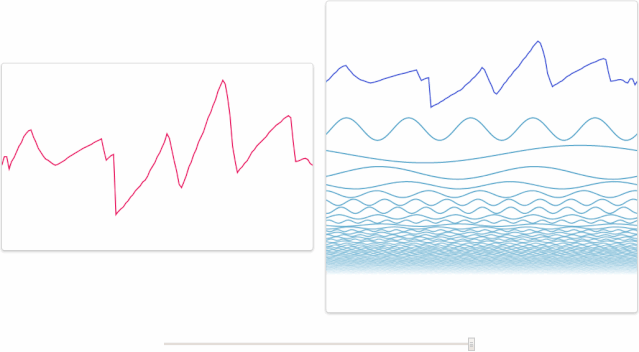
再比如，MP3文件格式正是基于這個原理運行的——為了節省空間，它把幾乎察覺不到的頻率部分舍棄掉了。只保留確定重要的頻率成分，丟棄那些不重要的部分，以(相當準確地)表現原始的音軌。盡管得出的波形與原始波形不一樣，但是聽起來將會和原始聲音很接近。

審核編輯：湯梓紅