至此,我們完整地分析了關斷瞬態過程中IGBT內部的空穴濃度分布變化從而引起的電荷存儲變化,而電荷對時間的變化率即對應電流。(6-47)是通過泰勒展開的一階近似得到的結果,而瞬態實際過程中需要更為精確的空穴濃度分布,才能獲得精確的電壓波形,下面我們對(6-47)進行修正。
首先,根據電荷守恒原則,先寫出空穴的連續性方程如下(空穴的變化等于體外流入的電荷與體內復合的電荷之和):
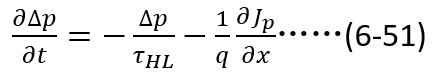
將(6-6)對 求導得到
求導得到 ,并代入(6-51),同時考慮到
,并代入(6-51),同時考慮到
1.IGBT器件內部電流處處相等,即 ,
,
2.大注入 ,化簡即可得到雙極型擴散方程,
,化簡即可得到雙極型擴散方程,

其中 。將(6-47)對時間求導,然后將(6-48)代入其中可以得到
。將(6-47)對時間求導,然后將(6-48)代入其中可以得到 ,
,

將(6-47)和(6-53)代入(6-52)得到擴散方程變形如下,

注,上述表達式中 的變量。
的變量。
將(6-54)對 兩次求積分,即可得到
兩次求積分,即可得到 修正表達式如下:
修正表達式如下:

系數 和
和 可以通過邊界條件,
可以通過邊界條件,  以及
以及 計算得到,如下,
計算得到,如下,

若將(6-56)代入(6-55),并分離 和
和 后可以得到
后可以得到
對比(6-47),顯然(6-57)多了一些修正項。在某時刻 ,若對(6-57)從
,若對(6-57)從 積分,再乘以
積分,再乘以 ,則可以得到瞬態過程中更為準確的電荷總量,積分過程略去,結果如下,
,則可以得到瞬態過程中更為準確的電荷總量,積分過程略去,結果如下,

對照(6-49),(6-58)多了一個修正項 ,一般情況下,
,一般情況下,  ,那么(6-58)就趨近于(6-49)了。
,那么(6-58)就趨近于(6-49)了。
由此可以看出,空穴電荷濃度分布既與基區寬度 有關,也與基區寬度隨時間的變化率
有關,也與基區寬度隨時間的變化率 有關;而電荷總量則只與基區寬度
有關;而電荷總量則只與基區寬度 有關。
有關。
更進一步地,只要準確得知 與
與 的時間維度表達式,那么就可以得知任意時刻的電荷濃度空間分布以及該時刻的電荷總量與時間的關系,當然這就與外圍拓撲電路相關,要得到具體的時間表達式,就需要針對不同的拓撲單獨討論。
的時間維度表達式,那么就可以得知任意時刻的電荷濃度空間分布以及該時刻的電荷總量與時間的關系,當然這就與外圍拓撲電路相關,要得到具體的時間表達式,就需要針對不同的拓撲單獨討論。
-
IGBT
+關注
關注
1278文章
4066瀏覽量
254412 -
電壓波形
+關注
關注
0文章
47瀏覽量
11099
發布評論請先 登錄
電機轉速異常,如何快速分析出占空比變化的趨勢
IGBT失效的原因與IGBT保護方法分析
大功率IGBT驅動的技術特點及發展趨勢分析
IGBT柵極電壓尖峰分析
討論一下IGBT的關斷過程
IGBT增大門極電阻,關斷尖峰會增加是怎么回事呢?
關于對IGBT關斷過程的分析

IGBT關斷時的電流和電壓

米勒電容對IGBT關斷時間的影響
igbt怎樣導通和關斷?igbt的導通和關斷條件
IGBT關斷過程分析
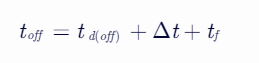





 IGBT的關斷瞬態分析—電荷存儲變化趨勢(3)
IGBT的關斷瞬態分析—電荷存儲變化趨勢(3)

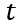











評論