在之前的文章中,我們研究了信號x(t)的傅立葉變換的一些特性。總結一下:

考慮到傅里葉變換是可逆的,我們可以寫成:
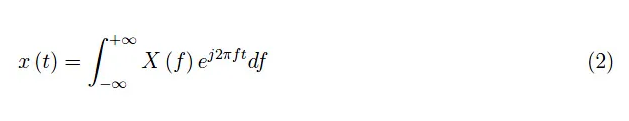
這個概念如圖1所示。
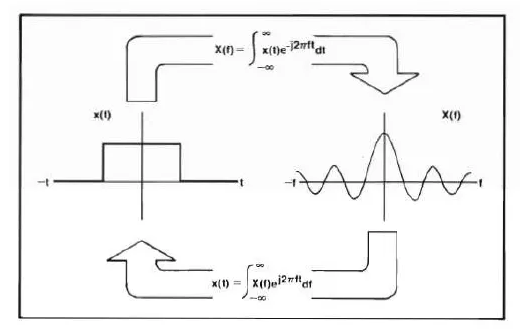
圖1:傅里葉變換的反演運算
單位脈沖
讓我們設想一個電路,它攜帶的電流在短時間內保持恒定值,然后消失。理想情況下,我們有:
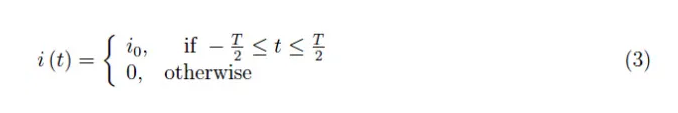
其中持續(xù)時間T足夠小。此外,我們假設i0=Q0/T,其中Q0是與電流i0值相關的電荷(圖2)。這個理想的實驗使我們能夠控制電流的持續(xù)時間T,同時保留電荷值。因此,通過減小T,我們得到如圖3所示的趨勢。
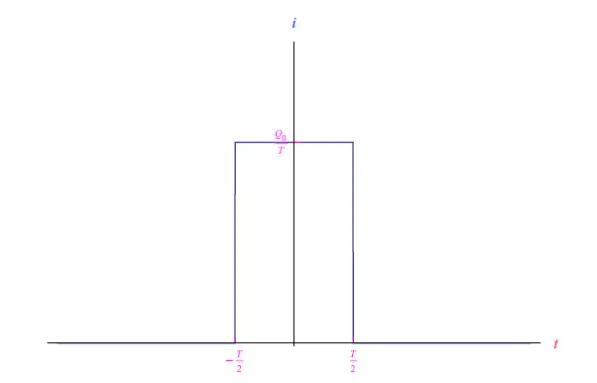
圖2:方程(3)的電流趨勢
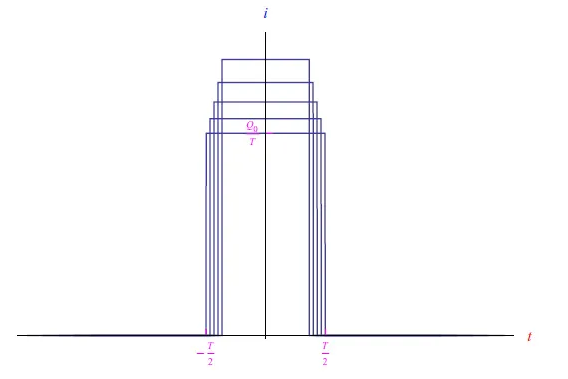
圖3:持續(xù)時間T值減小的方程(3)的電流趨勢。出于圖形的原因,我們僅針對起始值突出顯示i0/T
T的逐漸減小在數(shù)學上由極限通過運算表示:
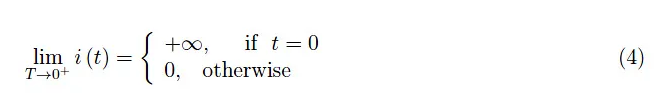
這顯然是無稽之談。然而,運算(4)中所涉及的電荷是Q0。事實上,電荷由下式給出:
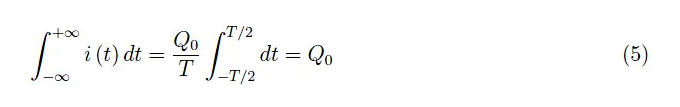
也就是說,圖2中與T無關的矩形的面積:
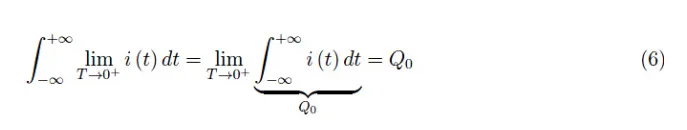
因此,“電流”(4)仍然與電荷Q0相關。由于(4)的模糊性,我們使用了引號。然而,結果(6)是顯而易見的,因為“電流”盡管有一個無窮大的峰值,但持續(xù)時間卻無窮小,并且我們知道0·∞也是無窮的形式,在這種情況下,它返回的是最終量Q0。用符號表示就是:

其中δ(t)是狄拉克δ函數(shù):

式(6)涉及:
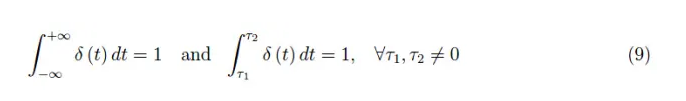
這一特性可概括為如下式子:

其中g(t)是任意正則函數(shù)。因此,積分值等于δ函數(shù)自變量消失時g(t)所假定的值。由此可見,對于一個平移的δ函數(shù),我們有:
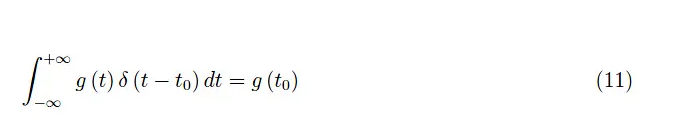
請注意,δ函數(shù)的量綱是其參數(shù)的倒數(shù)。因此,在我們的例子中,它具有時間的倒數(shù)(即頻率)的量綱。
根據(jù)δ函數(shù),電流(4)可以寫成如下:

這就是所謂的單位脈沖或數(shù)學脈沖(圖4)。
我們已經(jīng)考慮了電流的具體情況,但也可以考慮電壓。這里,單位脈沖可以寫為v(t)=Aδ(t),其中A是一個常數(shù),量綱為V·s。
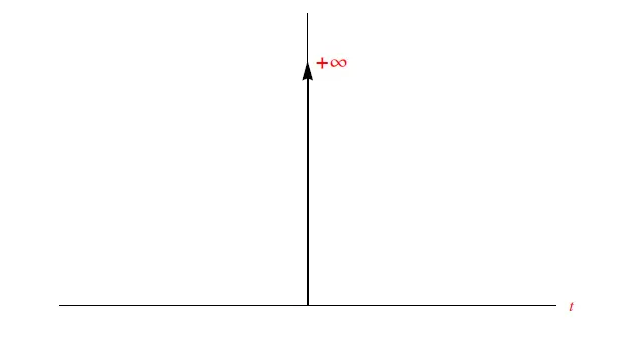
圖4:單位脈沖的圖形表示
傅里葉變換
任何單位脈沖在t=0處出現(xiàn)奇點都不會嚇到我們,因為脈沖在任何情況下都會在無窮遠處為零,因此我們預計傅里葉積分會收斂。事實上,對于特性(10),我們有:
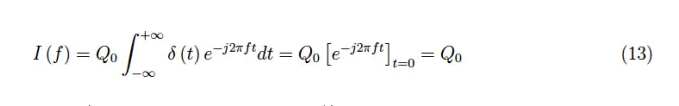
也就是說,單位脈沖的傅立葉頻譜是平坦的。從物理上講,這意味著單位脈沖可以分解為無數(shù)個從?∞到+∞的正弦頻率振蕩。
結論
為了定義單位脈沖,我們從矩形脈沖(3)開始,它在數(shù)學上更簡單。從正弦振蕩開始也能得到同樣的結果,正弦振蕩從?T/2處開始并在T/2處抵消。
我們建議讀者證明傅里葉變換是一個“sinc”函數(shù),即sin(f?f0)/(f?f0)類型,其中f0是截斷振蕩的頻率。通過減少后者的持續(xù)時間,sinc函數(shù)“變寬”,在T→0的極限范圍內變得嚴格平坦,從而再現(xiàn)了單位脈沖的傅里葉變換。相反,如果持續(xù)時間T逐漸增加,則sinc函數(shù)“收縮”,并且對于T→+∞為δ(f?f0),即以f0為中心的δ函數(shù)。這并不奇怪,因為我們現(xiàn)在有一個頻率為f0的從?∞到+∞的完整振蕩,因此傅里葉頻譜是一條以f0為中心的線,在數(shù)學上用δ(f?f0)表示。
我們的結論是,必須牢記以下雙重性:
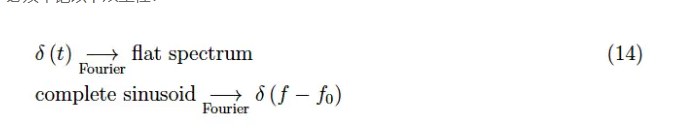
-
電流
+關注
關注
40文章
7136瀏覽量
135053 -
電荷
+關注
關注
1文章
653瀏覽量
36774 -
傅立葉變換
+關注
關注
3文章
105瀏覽量
32905
發(fā)布評論請先 登錄
用脈沖群衰減器檢驗電快速瞬變脈沖群發(fā)生器的脈沖電壓波形






 單位脈沖的傅立葉變換是否存在?
單位脈沖的傅立葉變換是否存在?












評論