從理論分析入手把握大規模神經網絡優化的規律,可以指導實踐中的超參數選擇。反過來,實踐中的超參數選擇也可以指導理論分析。本篇文章聚焦于大語言模型,介紹從 GPT 以來大家普遍使用的訓練超參數的變化。
規模律研究的是隨著神經網絡規模的增大,超參數、性能是如何改變的。規模律是對模型、數據、優化器關系的深刻刻畫,揭示大模型優化時的普遍規律。通過規模律,我們可以用少量成本在小模型上驗證超參數的選擇和性能的變化情況,繼而外推到大模型上。
在 LLM 中規模性常常變換模型大小和數據規模,進行大量調參而保持優化器不變。故對于大模型優化器而言,規模性是其性能很好的展現(性能上限)。設計更好的優化器(用更少的數據達到相同的性能)就是在挑戰現有的規模律。


神經網絡規模律
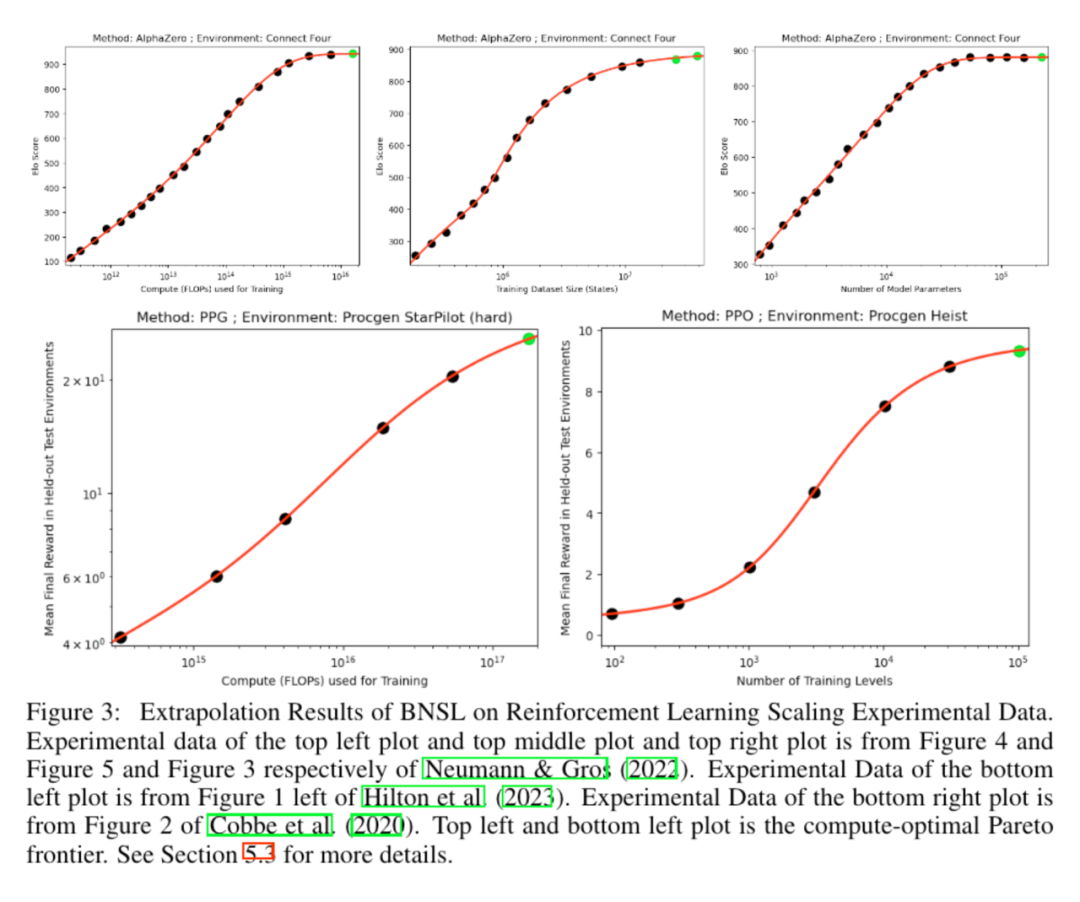
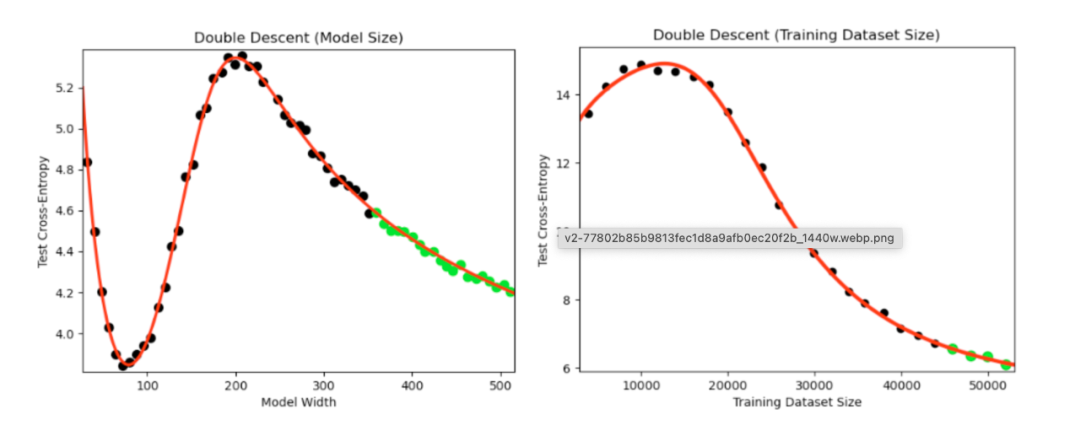
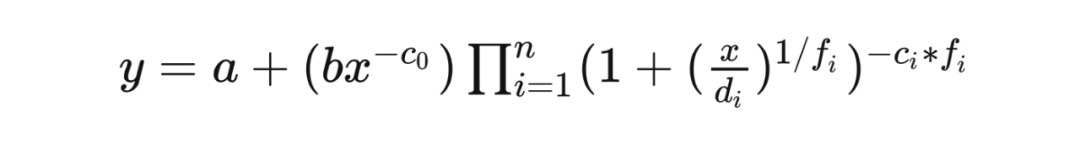
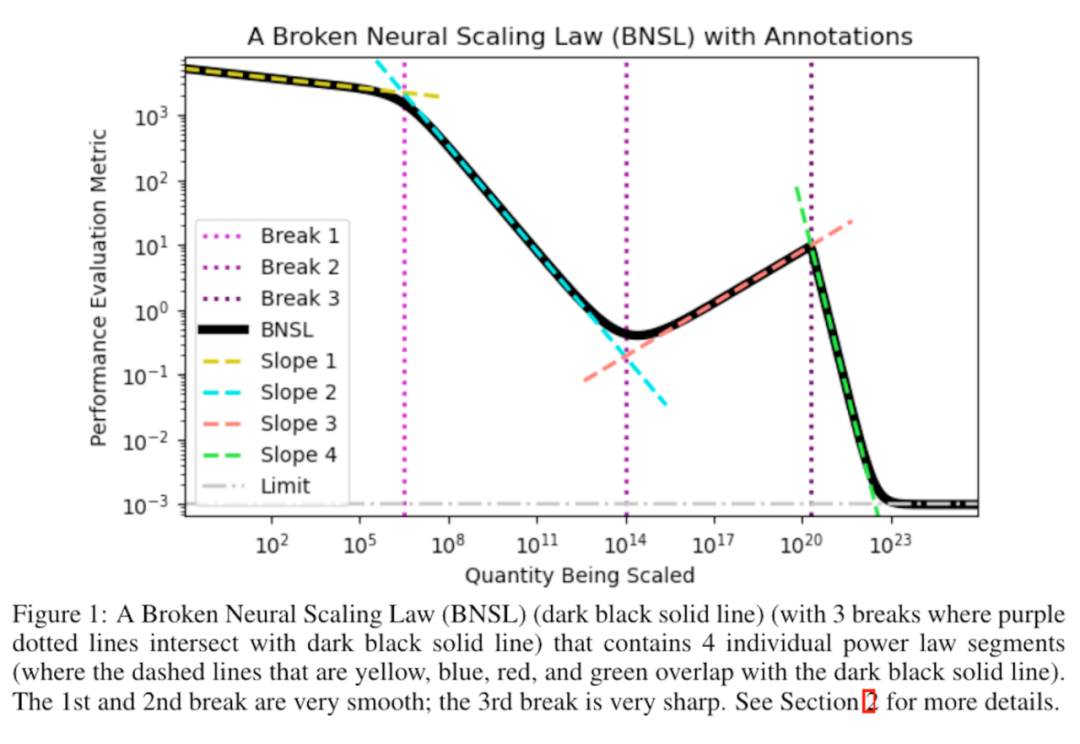

大語言模型規模律
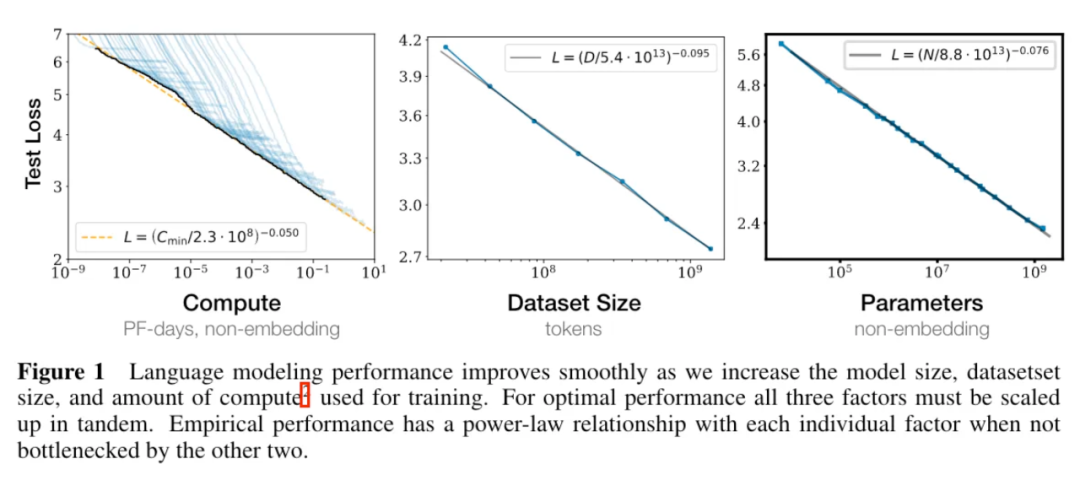
對不同的 沒有嘗試使用不同的學習率調整策略(正確的學習率調整策略對訓練影響很大) [KMH+20] 使用的 較小。規模性存在曲率,導致用太小的得到的結論不準確。(規模性存在曲率也說明了最終該規律會失效)
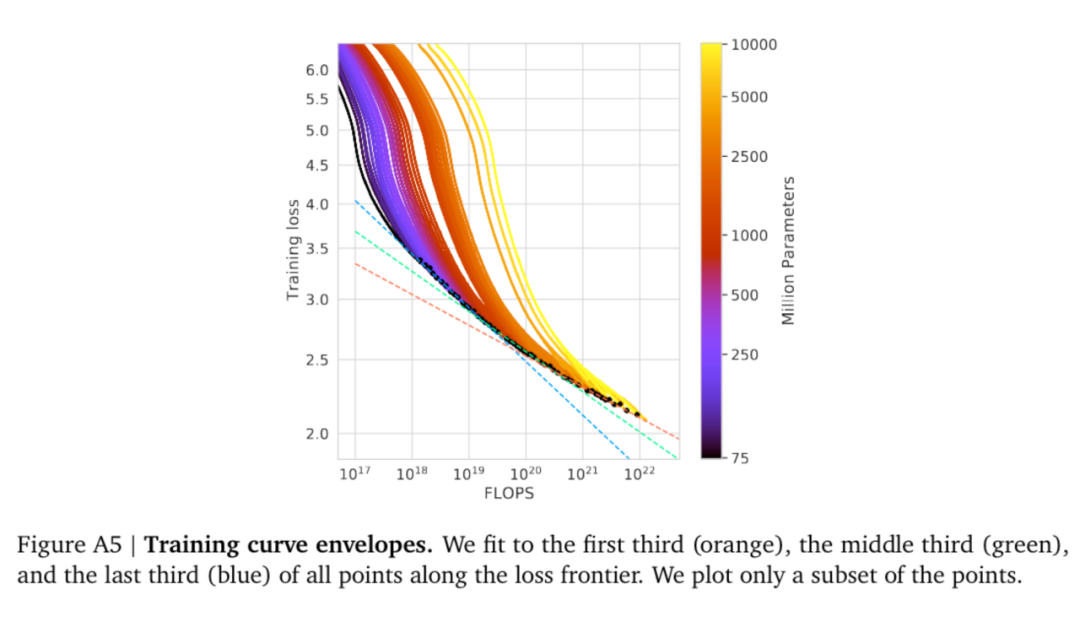
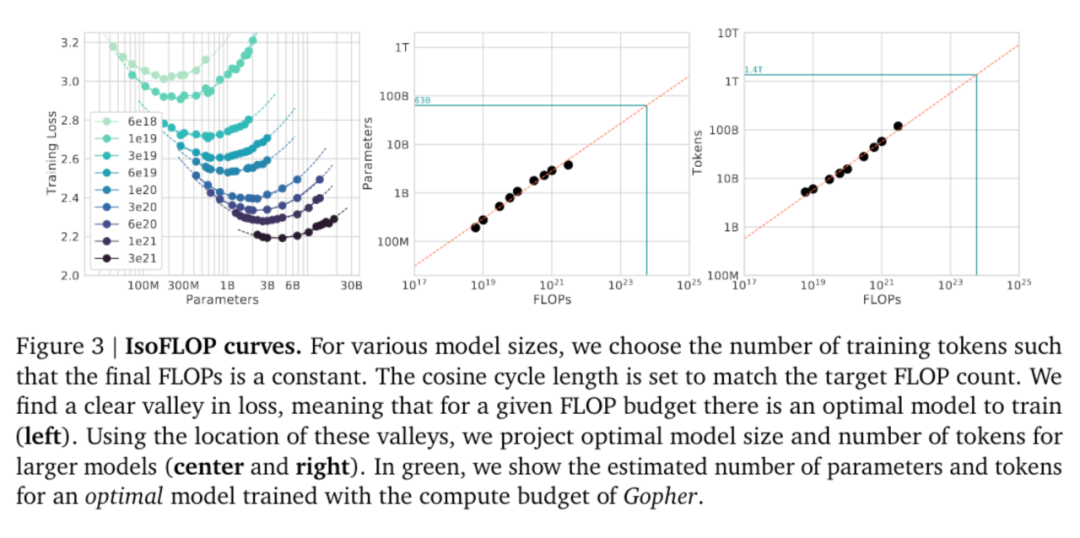
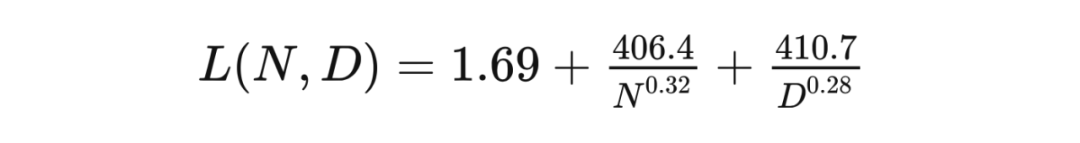
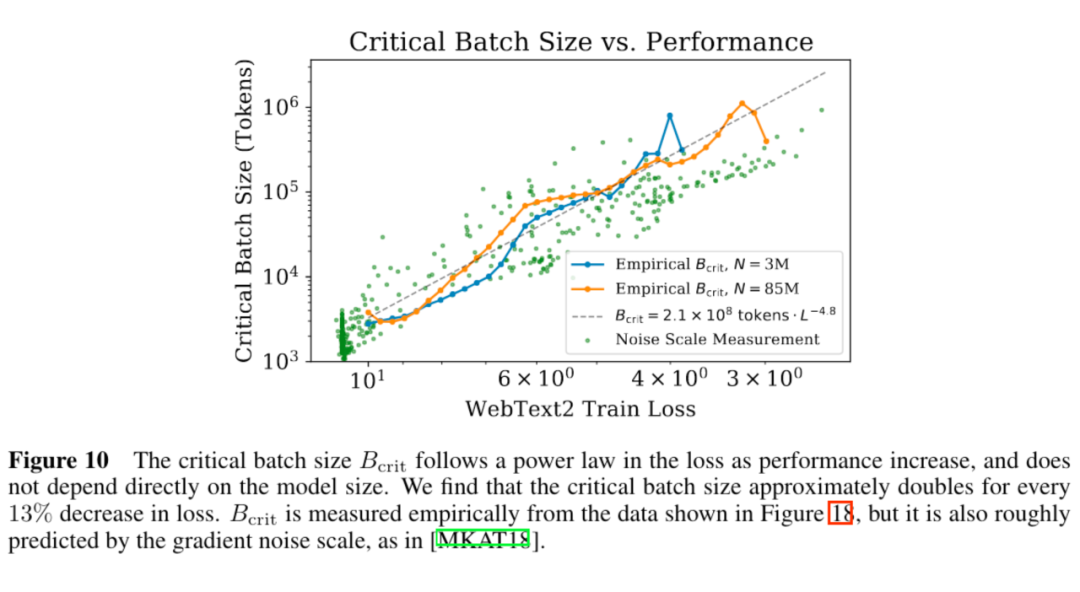
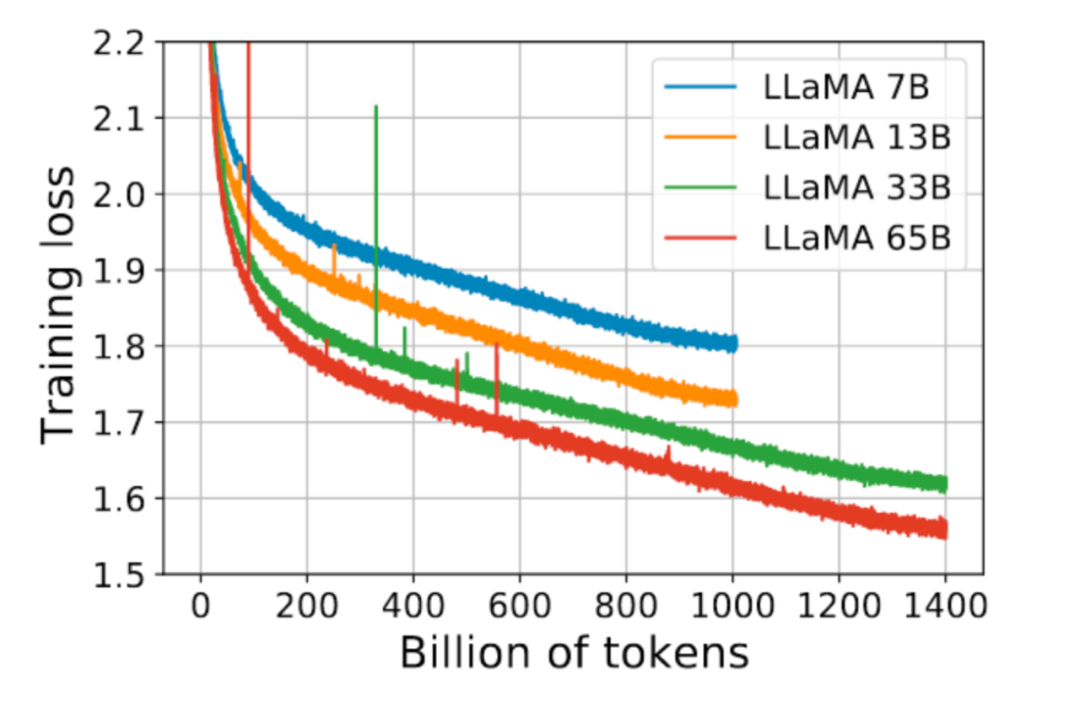
5. 模型的遷移泛化能力與在訓練數據集上的泛化能力正相關。
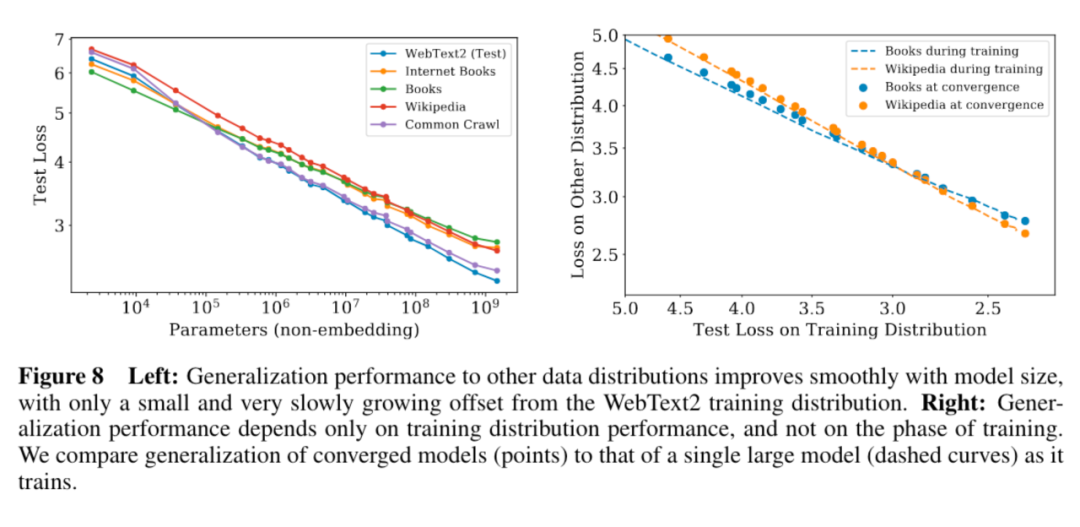
6. 更大的模型收斂更快(更少的數據量達到相同的損失)
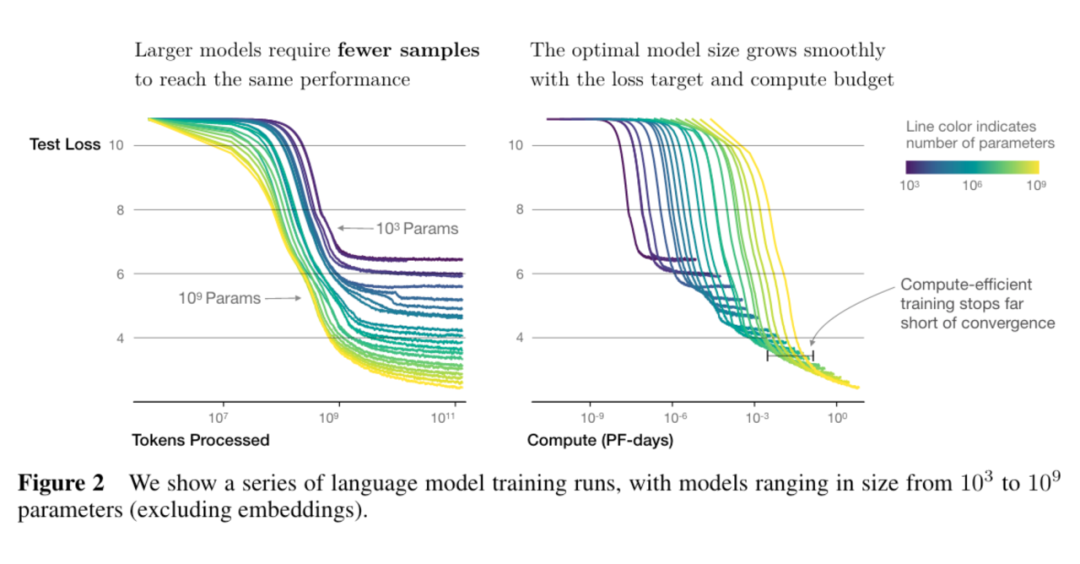

大語言模型規模律拾遺
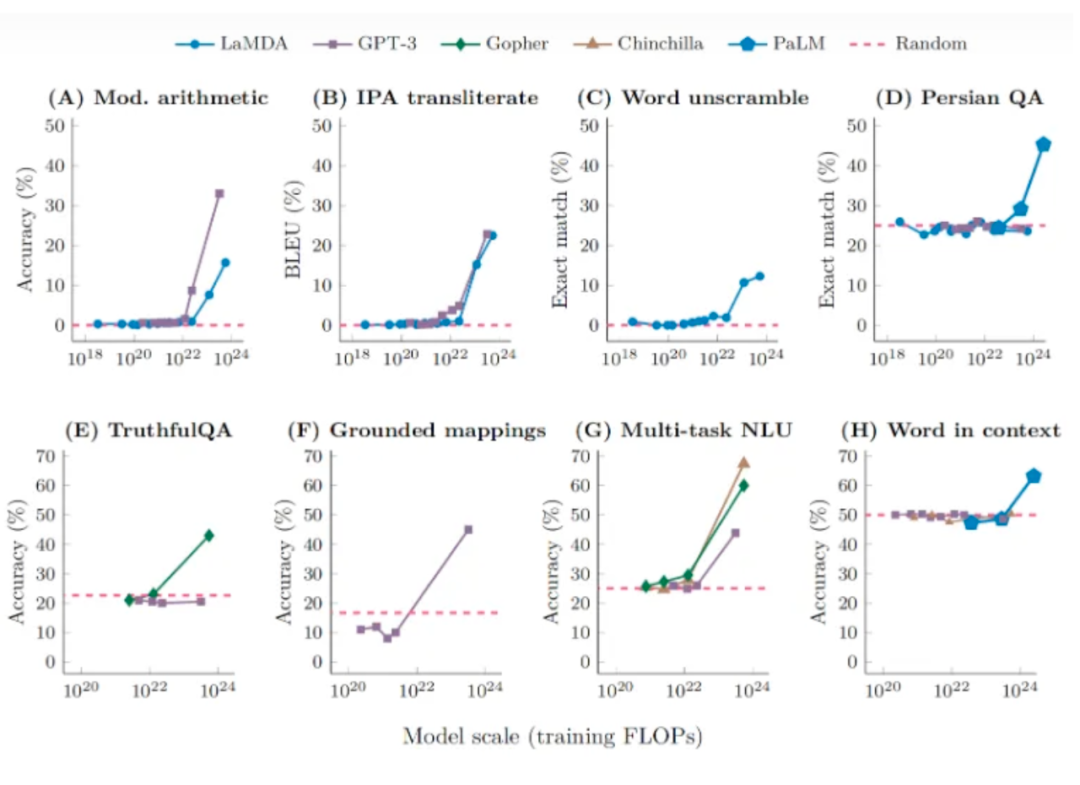
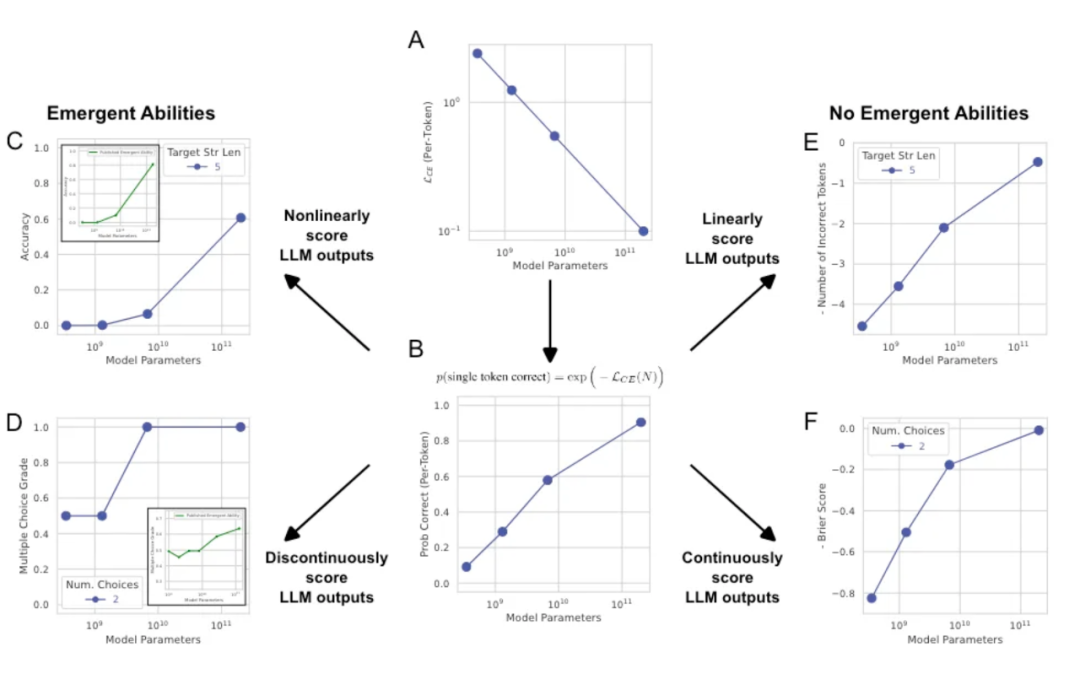
3.1 涌現是指標選擇的結果,連續指標與參數規模符合冪律分布
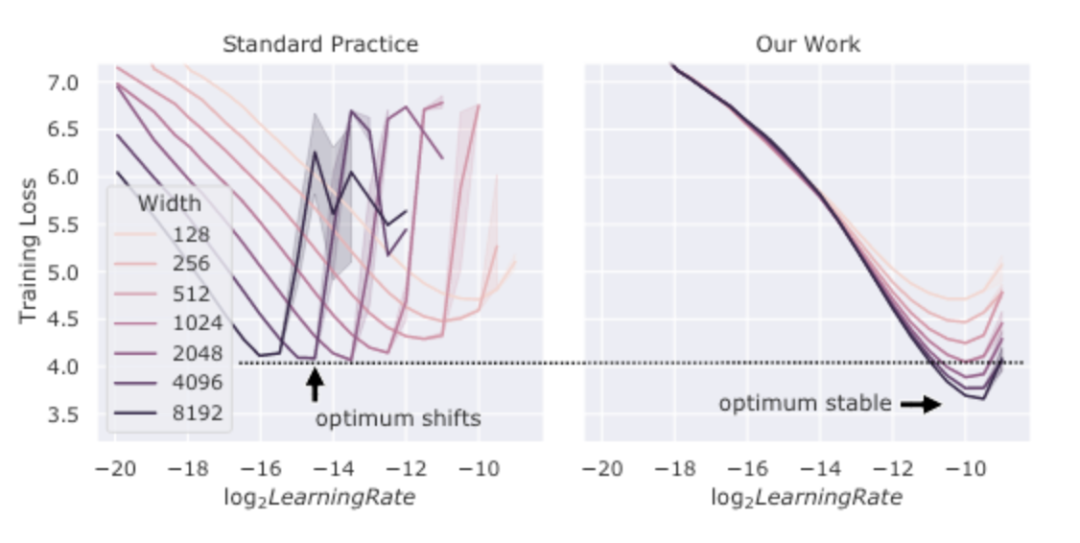
3.2 大模型需要更小的學習率
通過上文中的大模型參數經驗,我們很容易就發現大模型需要更小的學習率。[YHB+22] 在下左圖中展示了這點。其認為這是為了控制總方差在一定值(方差隨參數量以 增大)。對于這點筆者暫未找到詳細的理論解釋。[YHB+22] 中還提出了一種新的初始化和參數設置方法以保證不同規模的模型可以使用相同的學習率,這里不再展開。
3.3 使用重復數據訓練時(multi-epoch),應該用更多的輪次訓練較小的模型
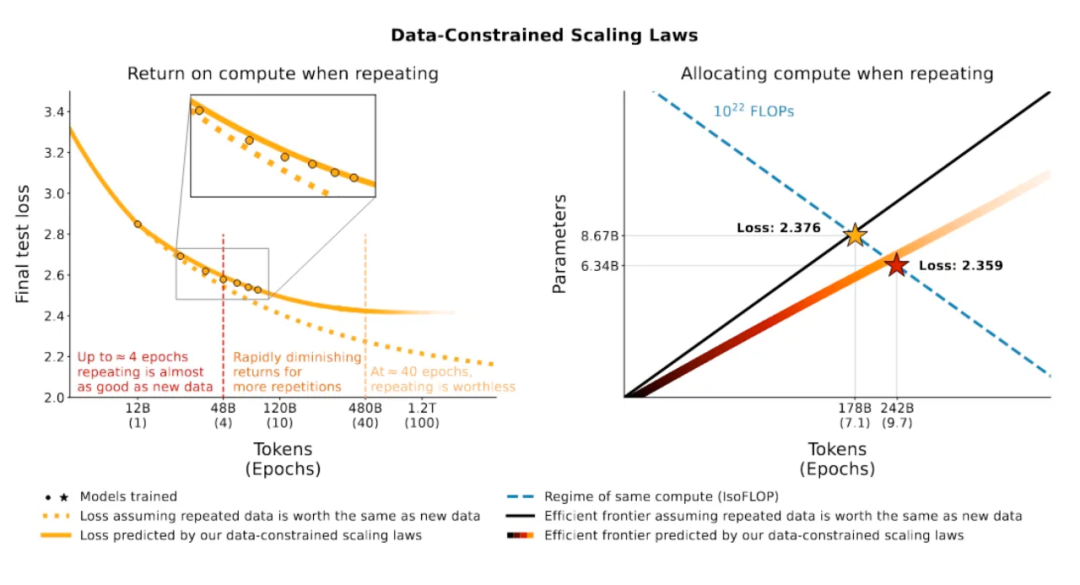
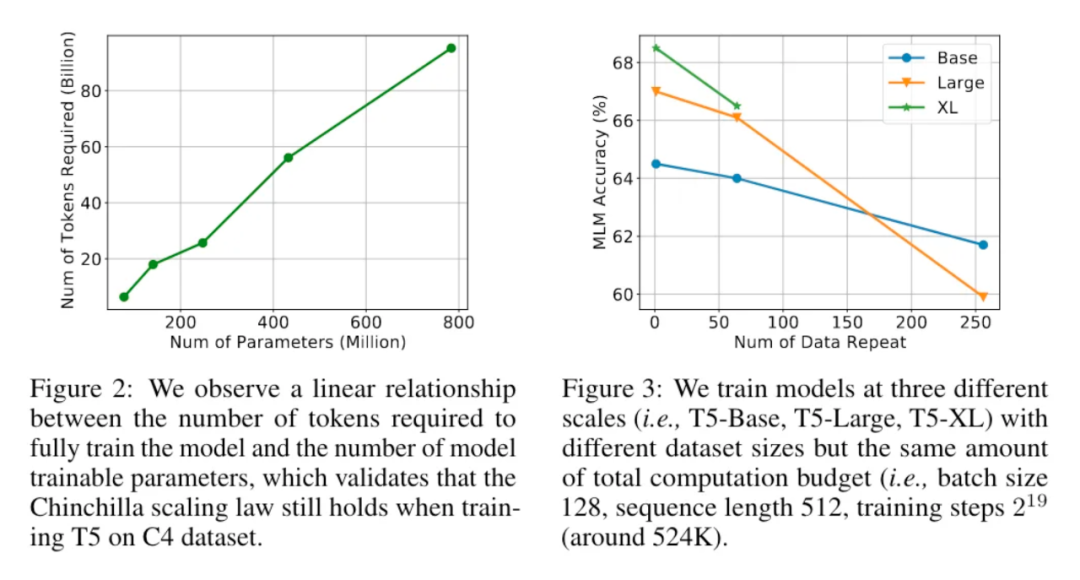
3.4 使用重復數據訓練對訓練幫助很小
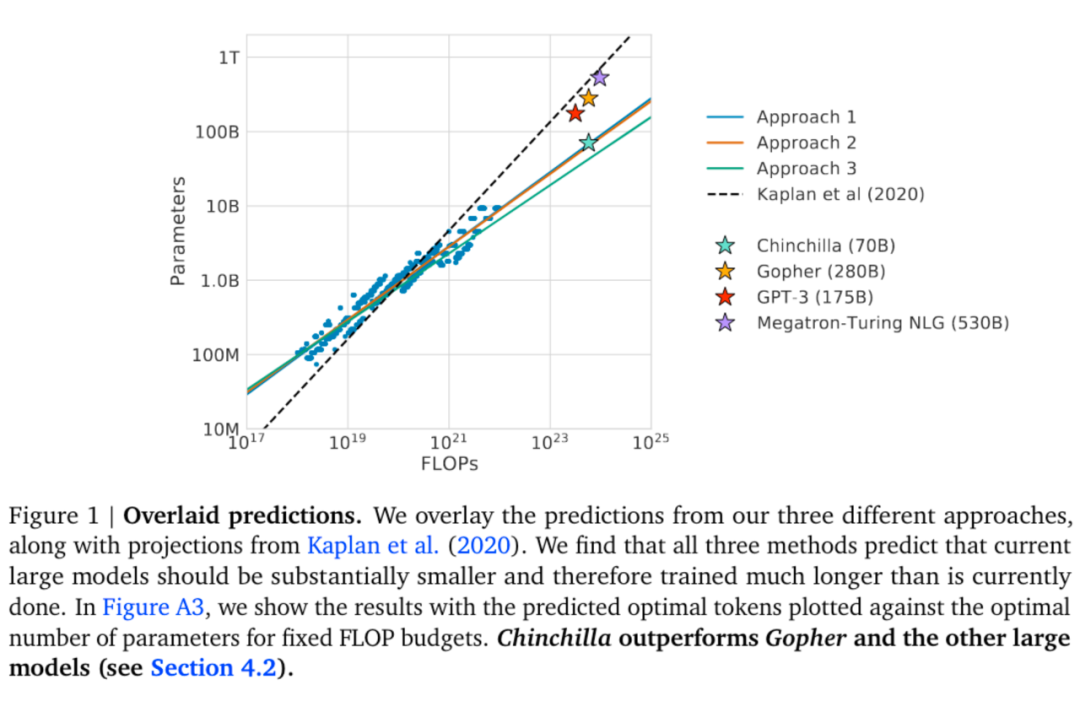
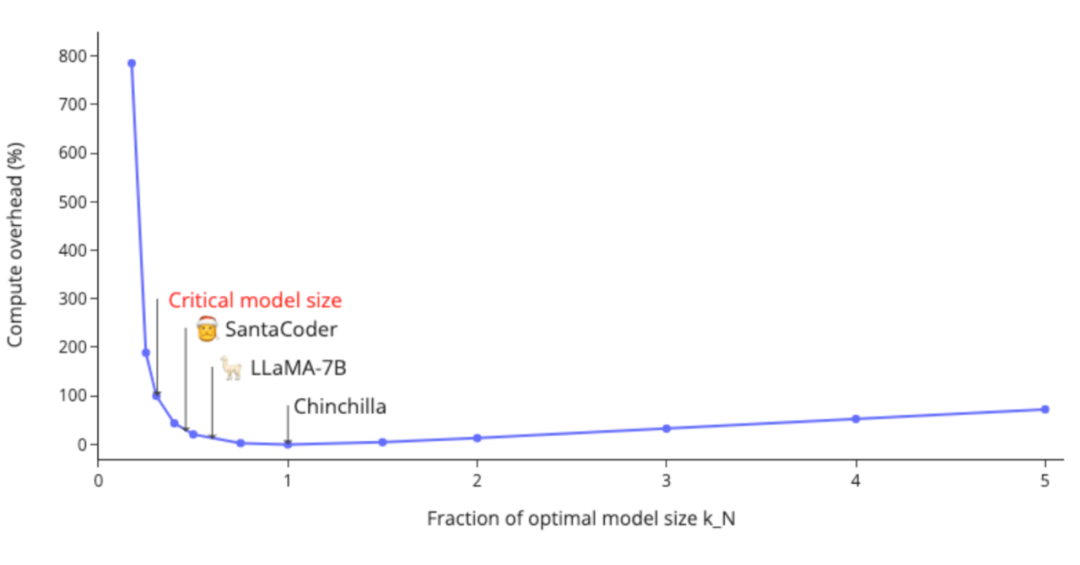
3.5 訓練比 Chinchilla 規模律更小的模型
Chinchilla 規模律的出發點是給定計算量,通過分配參數量和數據量最小化損失值。換言之,給定要達到的損失值,最小化計算量。然而在實際中,訓練一個小模型能帶來計算量(代表訓練開銷)以外的收益:
小模型部署后進行推理成本更小 小模型訓練所需的集群數量更少
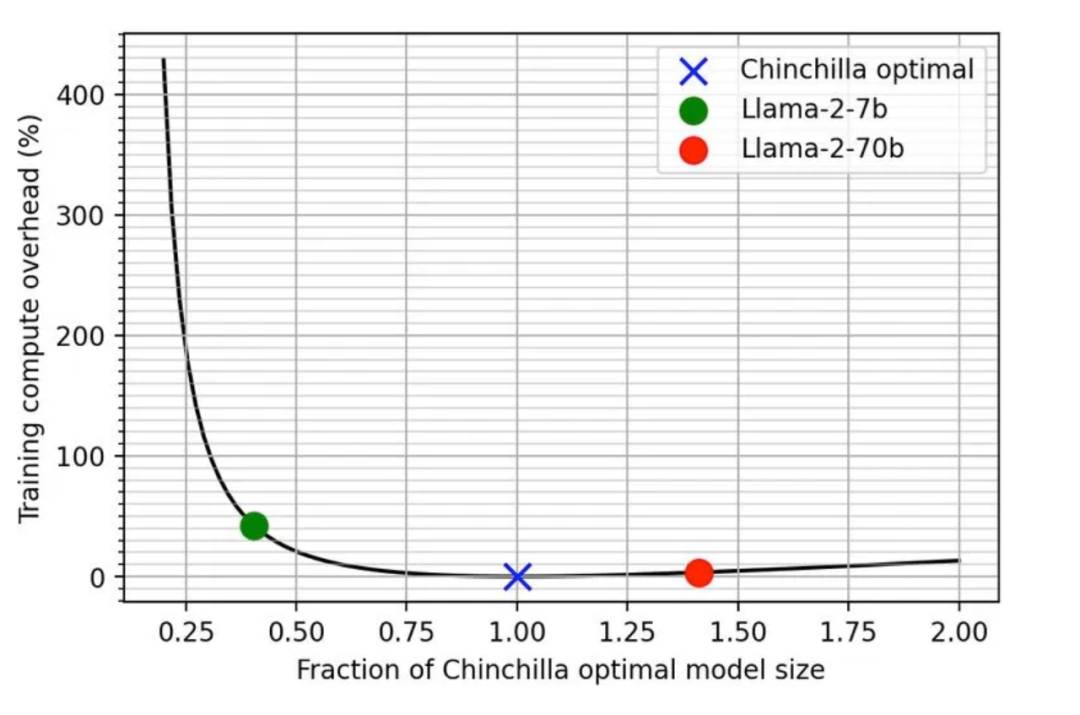
訓練所需的數據量不夠(正如 [XFZ+23] 指出的,我們正在用盡互聯網上所有的 tokens)。 小集群上訓練小模型需要更長的訓練時間(Llama2 500k its);如果使用大集群訓練則更困難(比如要使用更大的批量大小才能提高效率)。

LLM 的超參選擇
4.1 GPT(117M):
Adam lr:2.5e-4 sch: warmup linear 2k, cosine decay to 0 bs: 32k=64x512 its: 3M (100e) L2: 0.01 init: N(0, 0.02)
Adam(0.9,0.999) lr: 1e-4 sch: warmup 10k, linear decay to 0 bs: 128k=256x512 its: 1M (40e) L2: 0.01 dropout: 0.1
4.3 Megatron-LM(GPT2 8.3B & Bert 3.9B):
Adam lr: 1.5e-4 sch: warmup 2k, cosine decay to 1e-5 bs: 512k=512x1024 its: 300k L2: 0.01 dropout: 0.1 gradient norm clipping: 1.0
AdaFactor lr: 1e-2 sch: warmup constant 10k, sqrt decay bs: 65k=128x512 its: 500k (1e)
Adam(0.9, 0.95, eps=1e-8) lr & final bs: 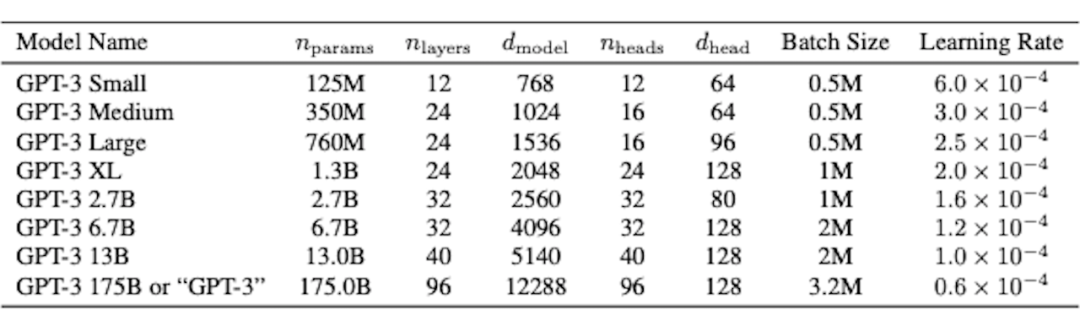
sch: warmup linear 375m tokens, cosine decay to 0.1xlr 260b tokens, continue training with 0.1xlr bs sch: 32k to final bs gradually in 4-12B tokens seq length: 2048 data: 680B gradient norm clipping: 1.0
Adam (Adafactor unstable beyond 7.1B) lr & final bs: 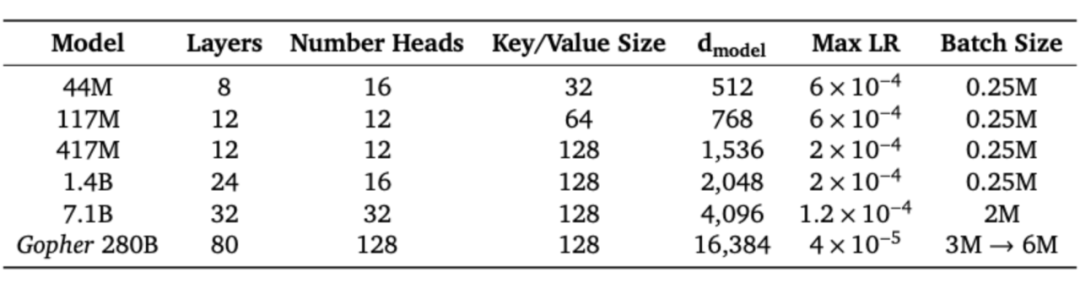
sch: warmup 1.5k, cosine decay to 0.1xlr gradient norm clipping: 0.25 for 7.1B & 280B, 1.0 for the rest
AdamW lr: 1e-4 bs: 1.5M to 3M others follow Gopher
Adam(0.9, 0.95) (SGD plateau quickly) lr & bs: 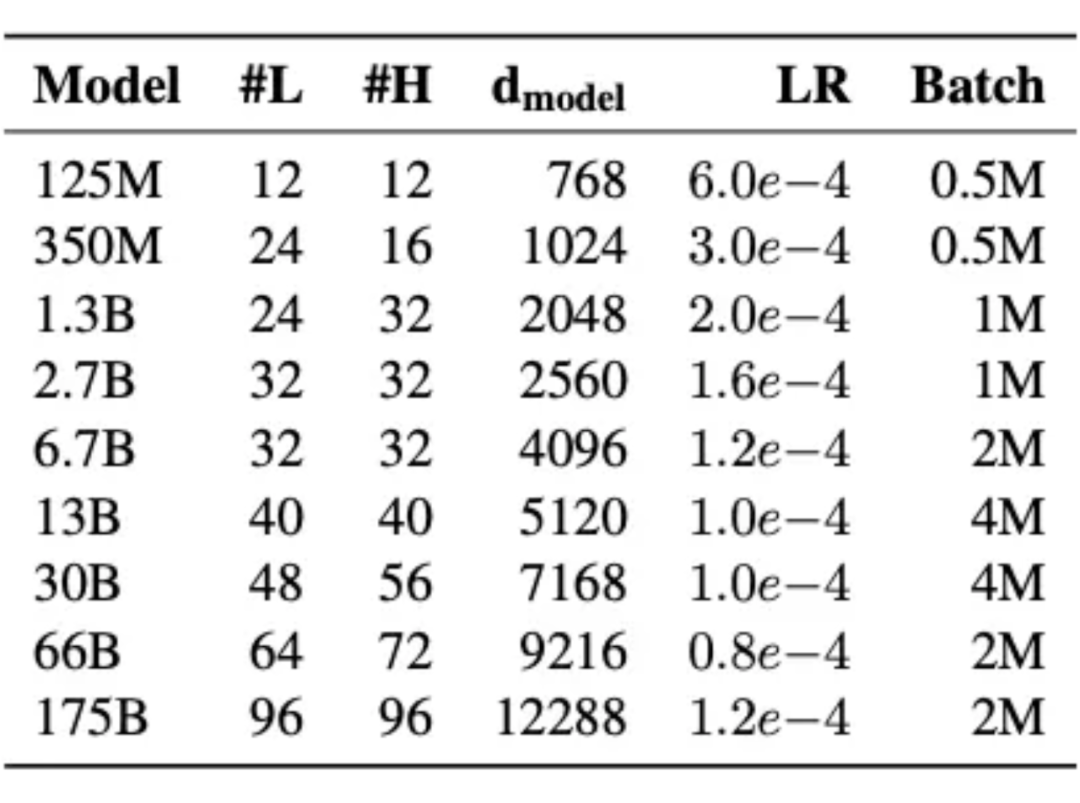
sch: warmup linear 2k, decay to 0.1xlr L2: 0.1 dropout: 0.1 gradient norm clipping: 1.0 init: N(0, 0.006), output layer N(0, 0.006*)
Adafactor(0.9, 1-) lr 1e-2
bs: 1M (<50k), 2M (<115k), 4M (<255k)
dropout: 0.1 gradient norm clipping: 1.0 its: 255kinit: N(0, embedding N(0,1)
AdamW(0.9, 0.95) lr & bs: 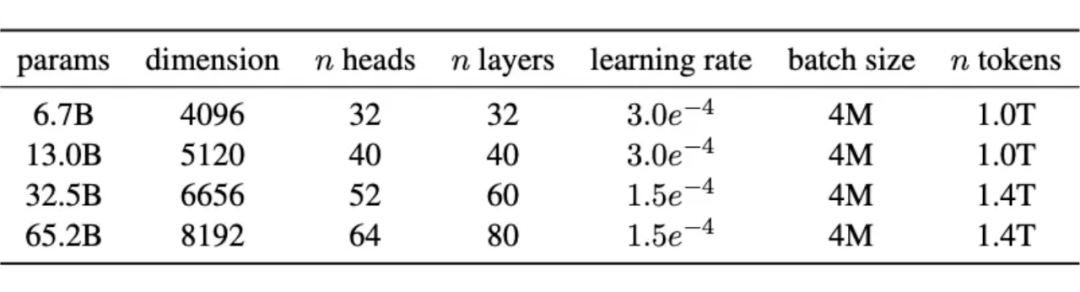
sch: warmup 2k, decay to 0.1xlr L2: 0.1 gradient norm clipping: 1.0
AdamW(0.9, 0.95, eps=1e-5) lr 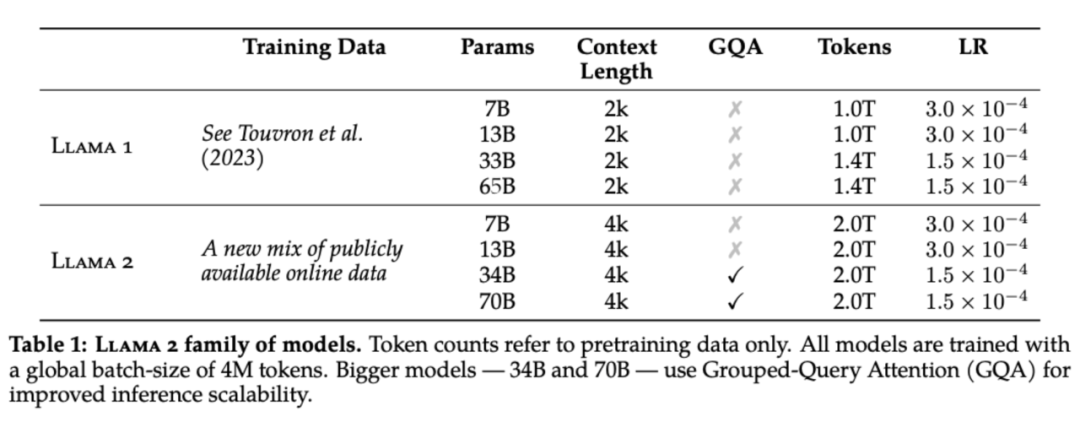
sch: warmup 2k, decay to 0.1xlr L2: 0.1 gradient norm clipping: 1.0
參考文獻
[ADV+23] Why do we need weight decay in modern deep learning?
[CGR+23] Broken neural scaling laws
[HBM+22] Training Compute-Optimal Large Language Models
[KMH+20] Scaling Laws for Neural Language Models
[SMK23] Are Emergent Abilities of Large Language Models a Mirage?
[YHB+22] Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer
[MRB+23] Scaling Data-Constrained Language Models
[XFZ+23] To Repeat or Not To Repeat: Insights from Scaling LLM under Token-Crisis
[H23]Go smol or go home
-
物聯網
+關注
關注
2930文章
46094瀏覽量
390277
原文標題:大規模神經網絡優化:超參最佳實踐與規模律
文章出處:【微信號:tyutcsplab,微信公眾號:智能感知與物聯網技術研究所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 大規模神經網絡優化:超參最佳實踐與規模律
大規模神經網絡優化:超參最佳實踐與規模律











評論