信號與系統 卷積 三角脈沖信號

簡 介： 根據信號與系統答疑過程中，學生對于三角形信號卷積結果的疑惑，給出了相應的數值、理論、以及頻譜分析的解答。特別是后面頻譜分析部分也是由另外參加答疑的同學提出的。之所以這個題目會產生疑問，主要原因來自于卷積計算“圖解法”所帶來的誤導。圖解方法只能幫助確定卷積的階段和積分上下限，求解卷積結果還是需要根據實際信號函數進行計算。

01 三角波卷積

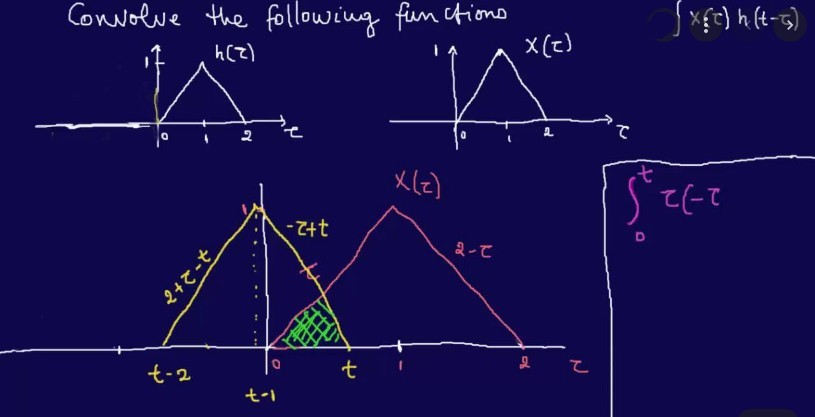
一、答疑碰到的問題

這兩天信號與系統期末考試答疑中，多次碰到學生詢問起一個課堂練習的習題。也就是為什么兩個等腰三角形的卷積是答案（C）：一個類似于升余弦的光滑曲線，而不是答案（B）一個尖頂的脈沖。此時才意識到這個問題的確有和直覺相違背的地方。

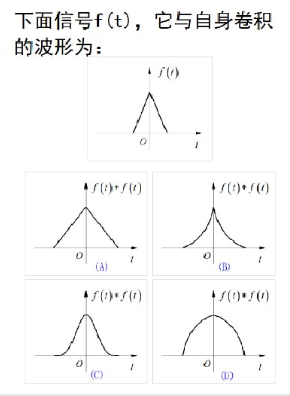
▲ 圖1.1.1 三角波與自身的卷積波形：選擇題

通過分析，造成判斷錯誤的來源，實際上是誤用了求解卷積過程中的“圖解法”。圖解方法通過把卷積的數學運算轉換成信號波形的變化，幫助確定卷積階段和積分的上下限。但往往也會對卷積結果產生誤導，即部分同學會將兩個圖像重疊對應的圖像面積當做求解的結果，但這種情況只能發生在一個信號是常量的情況。

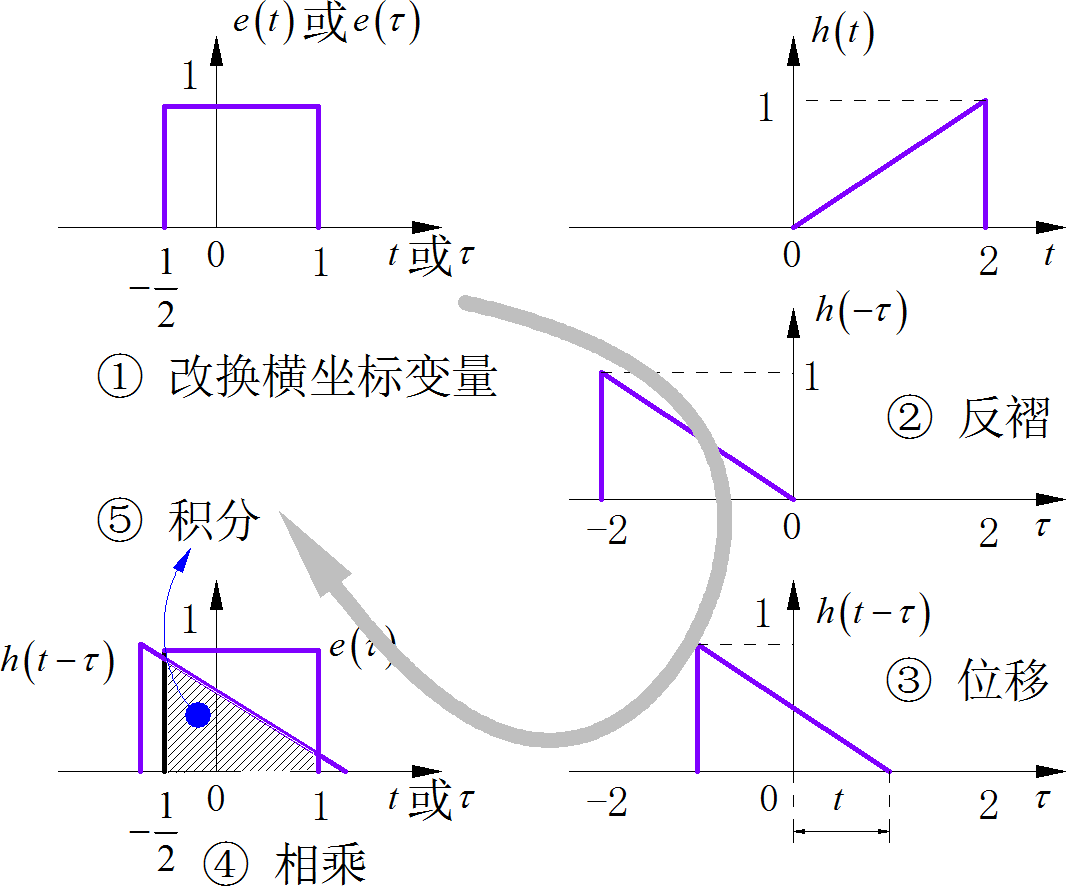
▲ 圖1.1.2 對于簡單信號所使用的圖解方法

二、問題分析

這兩天答疑過程中，學生也給出了對于這個問題很好的解釋。下面給出相應的總結：

1、數值求解

下面是通過數值求解反映的 一些等腰三角形與其自身卷積的結果，結果說明了兩個等腰三角學卷積的確是一個一階導數光滑的曲線。

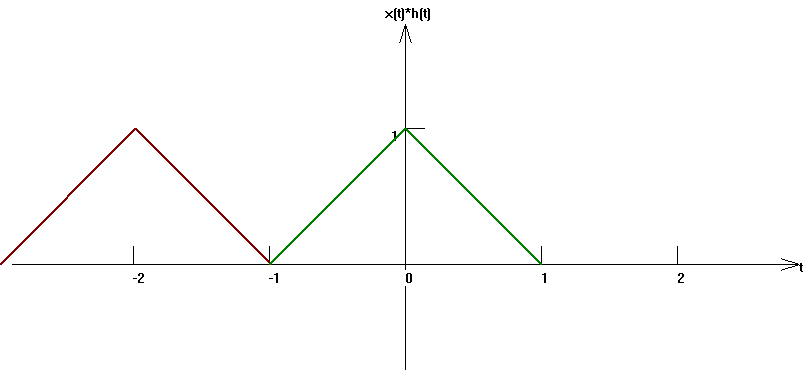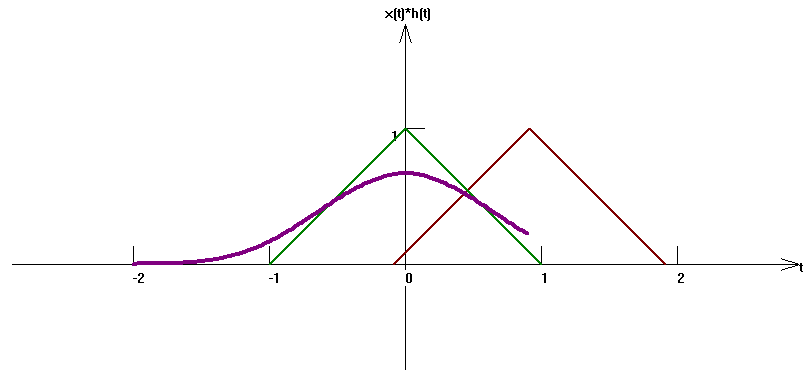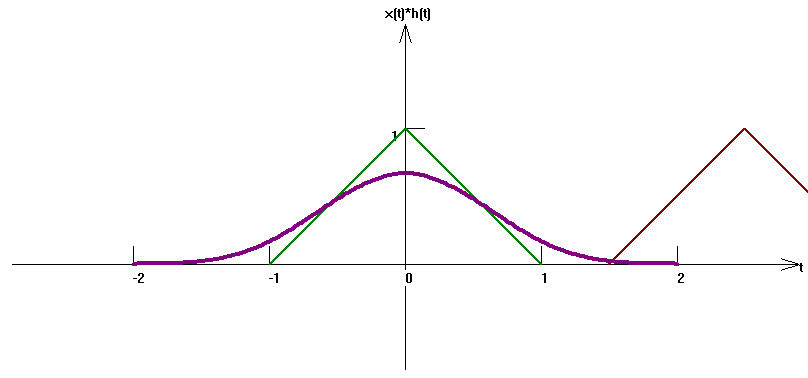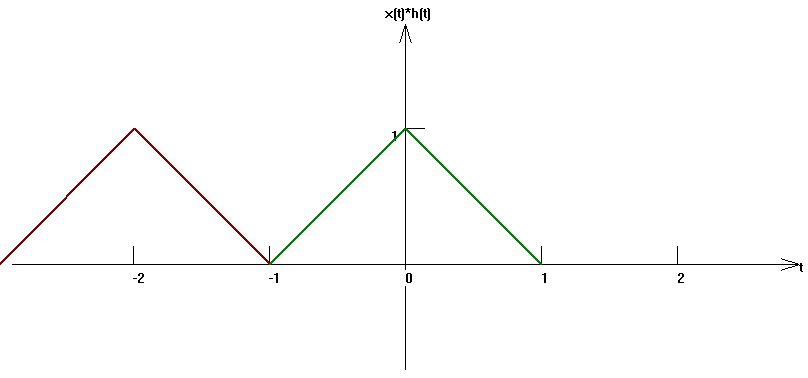
▲ 圖1 三角波與三角波相互卷積

2、理論分析

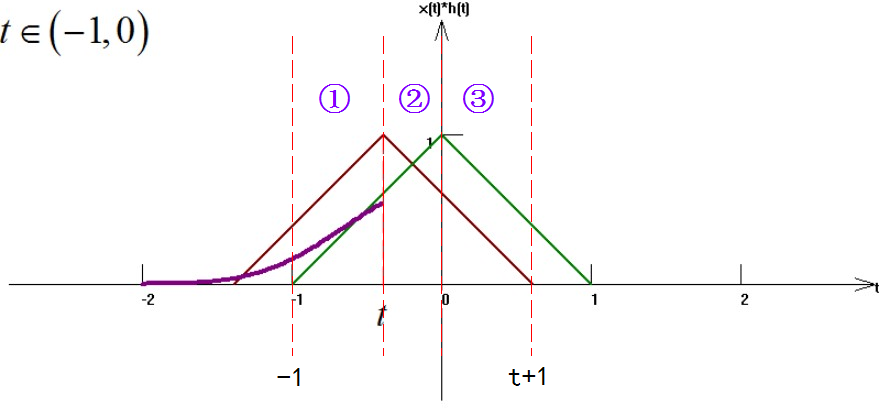
對于這類有限長度的簡單信號，在求解它們之間相互卷積的時候，同時使用“圖解法”幫助確定積分的區間。由于兩個三角波形自身都具有兩個變化階段一個是上升階段，一個是下降階段。它們的長度相同，所以通過簡單分析可以知道這兩個三角波卷積過程，它們重合情況可以分成四個階段，如下圖所示。當 不在這四個階段的時候，兩個三角形不重合，卷積結果為 0。

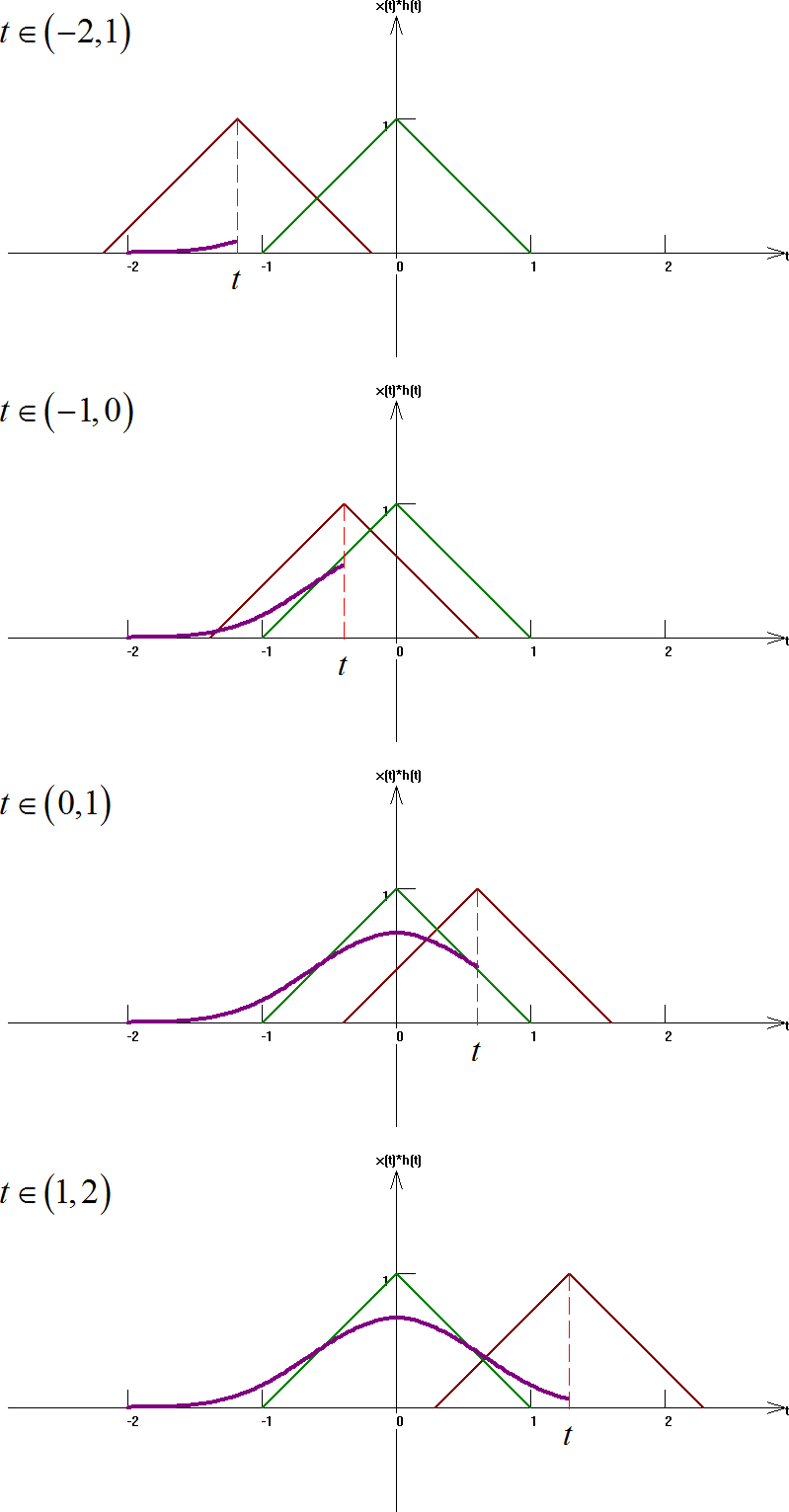
▲ 圖1.2.2 卷積過程中四個不同的重疊階段

由于參與卷積的信號左右對稱，所以只需要對于第一、第二階段進行求解；然后將結果偶對稱得到信號在 之后的結果。

（1）第一個階段

在 時，兩個三角形的重疊范圍是 。此時對應的卷積運算為

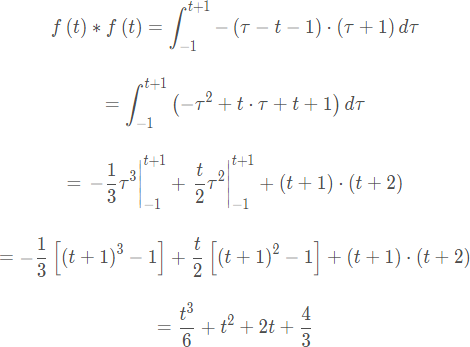
這個求解化簡過于繁瑣，使用Python中的符號求積分軟件包可以幫助進行求解

t,T=symbols('t,T')
result=integrate(-(T-t-1)*(T+1),(T,-1,t))

（2）第二階段

在 ，參與卷積的信號重疊方式為如下圖所示，重疊區域為 。

合并前面求解的第一、第二階段的公式，將它們進行反褶之后，便可以得到第三、第四階段的公式。最終三角形卷積的結果為：

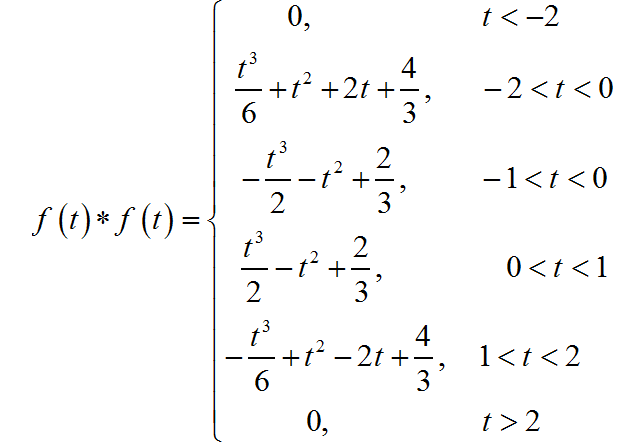
（3）數值驗證

下面使用Python對上述公式進行繪制，查看卷積結果的信號波形。

defw(t,t1,t2):
 returnheaviside(t-t1,0.5)-heaviside(t-t2,0.5)
deff1(t):
   returnt**3/6+t**2+2*t+4/3
deff2(t):
 return-t**3/2-t**2+2/3
deff(t):
    returnf1(t)*w(t,-2,-1)+
   f2(t)*w(t,-1,0)+
 f2(-t)*w(t,0,1)+
 f1(-t)*w(t,1,2)

t=linspace(-2,2,500)
fdim=f(t)
plt.plot(t,fdim)
plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.tight_layout()
plt.show()

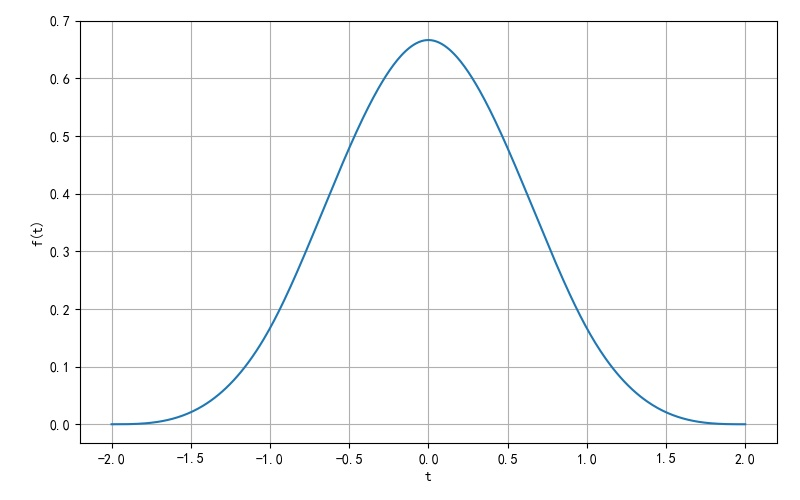
3、傅里葉變換

可以利用傅里葉變換卷積定理，分析兩個三角脈沖信號的卷積。對于高度為 1，寬度為 2 的對稱等腰三角型，對應的頻譜為

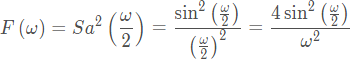
卷積結果對應的頻譜為：

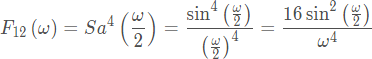
當然，直接從上面結果進行傅里葉反變換求解卷積時域表達式也比較麻煩，不過它可以告訴我們，卷積結果的頻譜幅度衰減的規律應該是 。再由信號波形的光滑性與頻譜衰減之間的關系可知，卷積結果應該是滿足二階導數連續。由此也可以幫助判斷在選擇題中，只有答案（C）能夠滿足二階導數連續的要求，其它三個信號波形對應的一階導數都不連續。

審核編輯：湯梓紅