Allan方差起初是為了評估原子鐘振蕩器的穩定性而提出的,它提供了在不同時間尺度上頻率穩定性的可靠測量,而標準偏差等統計量卻沒有考慮到這一點。在本白皮書中,我們將回顧 Allan 方差的數學基礎,并分享Allan 方差及其相關參量如何在振蕩器表征等實際應用中成為精確分析時間序列數據的有用工具。
利用Moku 我們可以執行Allan 方差測量,Moku 是一種基于 FPGA 的設備,它包含了一整套可重構的測試測量儀器。相位表是Moku上開發的高精度數字相位測量儀,我們可以超精確地記錄輸入周期信號的相位、頻率和振幅數據,也可以實時地計算和繪制 Allan 方差統計數據。
Allan方差由來
您的系統穩定性如何?有許多工具可以用來解答這個問題。1960年 David W. Allan 在在美國國家標準技術研究院(當時稱為國家標準局)研究光學時鐘時發明了一種全新的工具[1]。
Allan 發現,隨著樣本數量增加,現有的統計指標(例如標準差)對于特定噪聲源會出現偏差。這促使他開發了一種新的時域計量方法,今天該方法以他的名字命名。
由于 Allan 當時研究光學時鐘,所以為原子頻率鐘標準開發了 Allan 方差。因此,該主題的討論經常僅限于該領域的術語,特別是在表征振蕩器的頻率穩定性方面。
但是,Allan方差可以針對任何時間序列進行計算。該序列可以代表信號自身,像溫度傳感器的輸出信號,或其任意屬性(如頻率、相位、幅度等),并以恒定的速率進行評估。因此,Allan 方差從通信[2]到導航[3]的各種應用中備受青睞。
Moku 相位表提供了 Allan 方差作為一個數據后續處理的選項,如下方圖 1 Moku:Pro 相位表所示。本說明針對首次接觸的用戶提供了有關該統計方法的入門介紹。
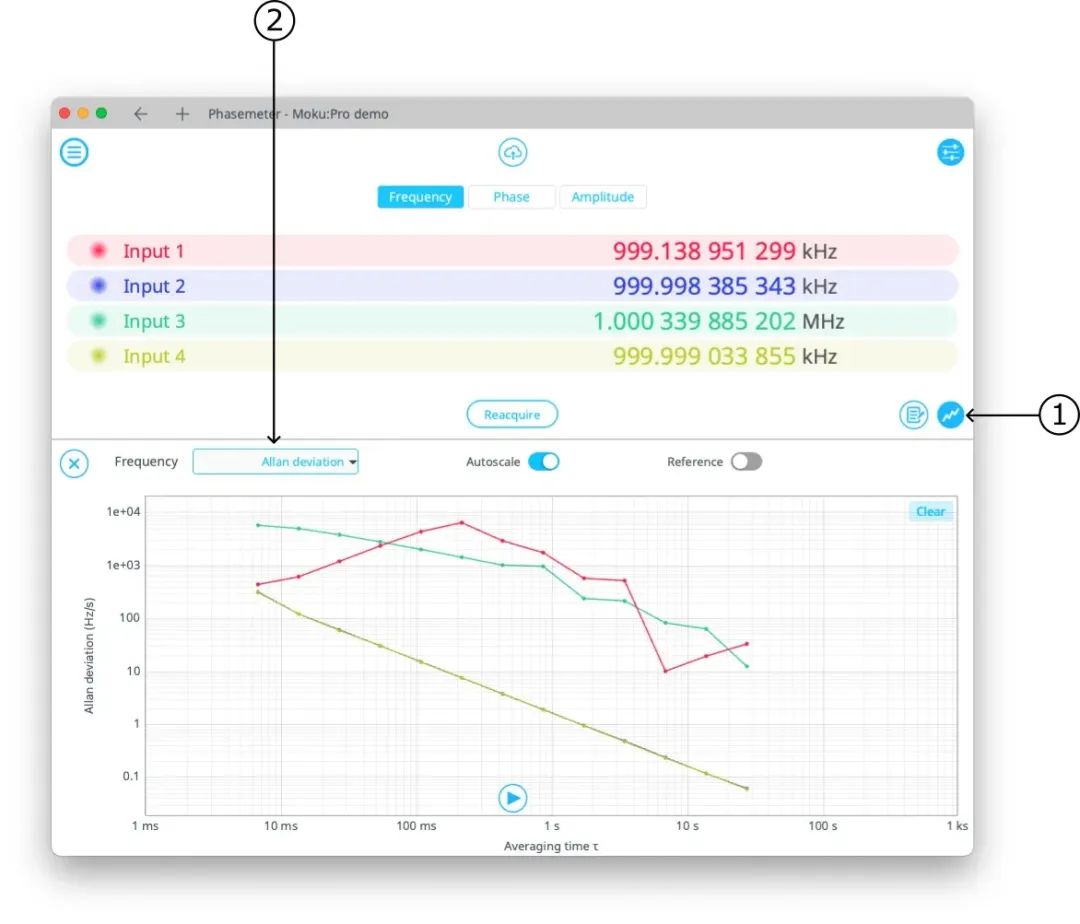 圖 1:在相位表上顯示 Allan 標準差(Allan 方差的平方根),首先單擊數據圖形顯示按鈕。然后從下拉菜單選擇“Allan 標準差”。
圖 1:在相位表上顯示 Allan 標準差(Allan 方差的平方根),首先單擊數據圖形顯示按鈕。然后從下拉菜單選擇“Allan 標準差”。
Allan方差數學運算
Allan 方差的基本原理是將時間序列劃分為等分的部分,并考慮每等分的時間平均值與前一等分的時間平均值有何不同。如果從整個數據集來看這些差異很小,那么系統在這個時間尺度上是穩定的。
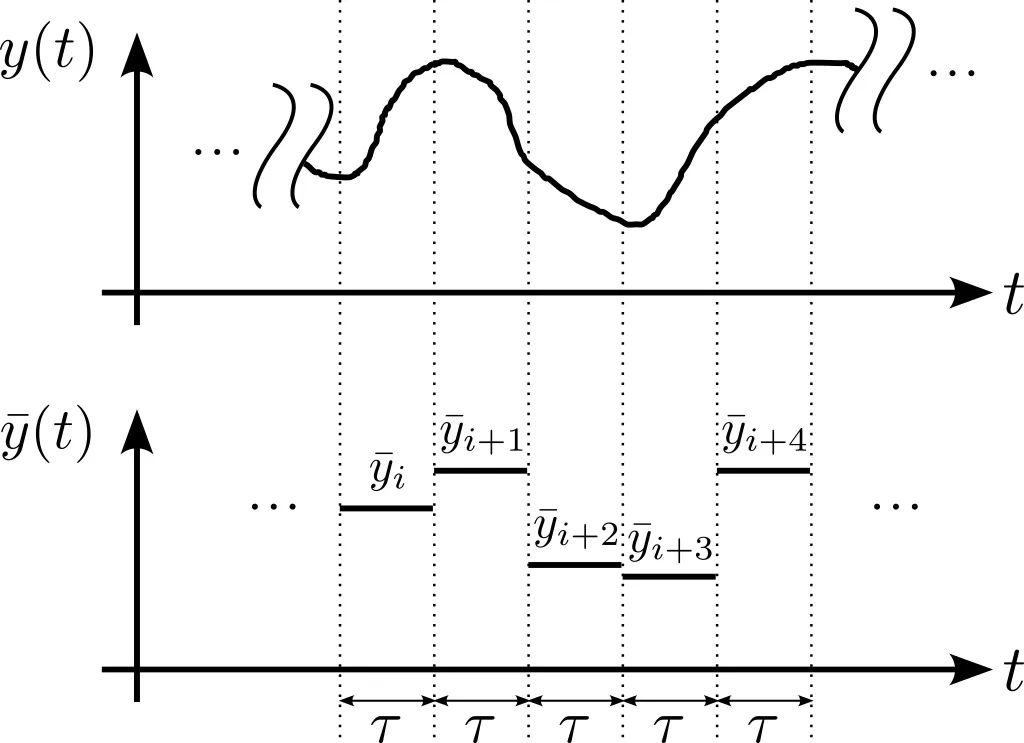
圖2:計算 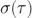 第一步是將數據分割成長度為τ的片段并計算每一個分段的時間平均值,。然后,我們減去連續平均值并計算這些差異的 RMS 值。將計算結果除以
第一步是將數據分割成長度為τ的片段并計算每一個分段的時間平均值,。然后,我們減去連續平均值并計算這些差異的 RMS 值。將計算結果除以 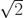 得到觀測時間τ上的 Allan 方差。
得到觀測時間τ上的 Allan 方差。
更具體地說,假定我們有一個連續的時間序列 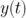 ,其Allan方差
,其Allan方差 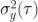 定義為:
定義為:
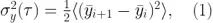
這里<.>表示期望值<平均值>,同時是 y 在觀測時間τ上的第 i 個樣本的平均值(圖 2)。Allan 標準差就是Allan 方差的平方根,或者 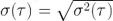 。我們可以針對一系列觀測時間τ評估該表達式,以深入了解數據在不同時間尺度上的自相似性(即穩定性)。
。我們可以針對一系列觀測時間τ評估該表達式,以深入了解數據在不同時間尺度上的自相似性(即穩定性)。
從式(1)可以看出,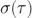 的維度與 y 相等。我們將該值解釋為間隔τ秒的 y 測量值在兩個τ秒之間的預期均方根差。
的維度與 y 相等。我們將該值解釋為間隔τ秒的 y 測量值在兩個τ秒之間的預期均方根差。
例如,假定一個時鐘振蕩頻率在 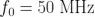 。如果其分數頻率差的 Allan 方差- Y,表達式為:
。如果其分數頻率差的 Allan 方差- Y,表達式為:
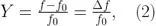
在10秒觀測時間(τ= 10 s)上為 1.23x10-10,然后我們可以預計 Y 其兩個隨機選擇并連續的 10秒觀測時間測量值相差為 1.23x10-10 RMS。在給定的部分頻率差定義下,這等于一個預期的絕對頻率差 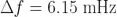 。
。
現在我們思考長度為 M 的真實有限數據集的情況,以周期進行采樣(圖 3)。我們不能在一個采集系統內自由地選擇總時間τ,所以我們將時長 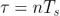 劃分成K個數據分段,這里
劃分成K個數據分段,這里 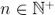 。Allan 方差可以粗略地近似為:
。Allan 方差可以粗略地近似為:
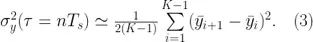
這里在 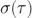 的不確定度是
的不確定度是 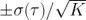 。測量不確定度的完整處理方法不在本文討論范圍之內,因此請參閱參考文獻[4]了解更多詳細信息。為了改善結果的可靠性并且比較高效地使用數據值,我們可以將數據劃分為重疊段(圖 4),這得到了
。測量不確定度的完整處理方法不在本文討論范圍之內,因此請參閱參考文獻[4]了解更多詳細信息。為了改善結果的可靠性并且比較高效地使用數據值,我們可以將數據劃分為重疊段(圖 4),這得到了 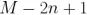 對連續的分段,與之前的
對連續的分段,與之前的 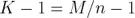 正相反。這樣重疊的 Allan 方差可以表示為:
正相反。這樣重疊的 Allan 方差可以表示為:
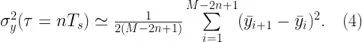
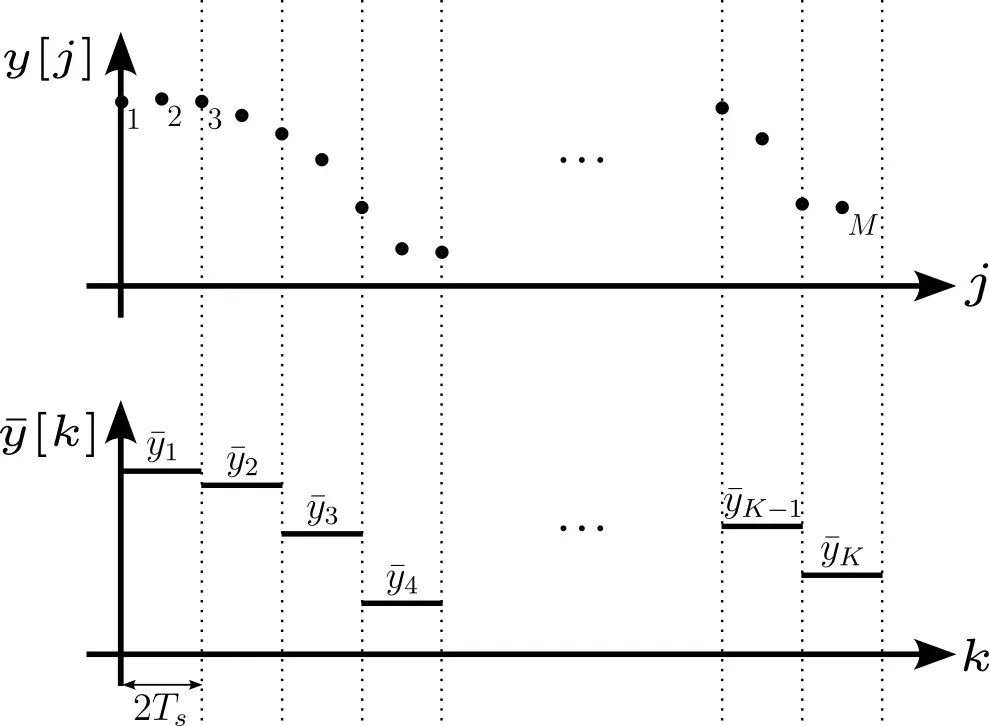
圖 3:在真實的采樣系統里,數據量是有限的,同時τ被限制在幾倍采樣周期內 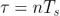 (這里n = 2)
(這里n = 2)
通過積分獲得Allan方差
在許多常見的測量場景下存在一個變量 x,其屬性如下式所示:
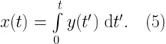
例如在時鐘穩定度測量中,時間偏差 X 是部分頻率差 Y 的積分,例如在陀螺儀系統中,被測角度,θ即旋轉速度Ω的積分。
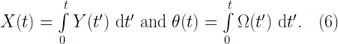
我們可以通過式(5)的積分來計算 x,即使它不和某個被測物理量相對應。
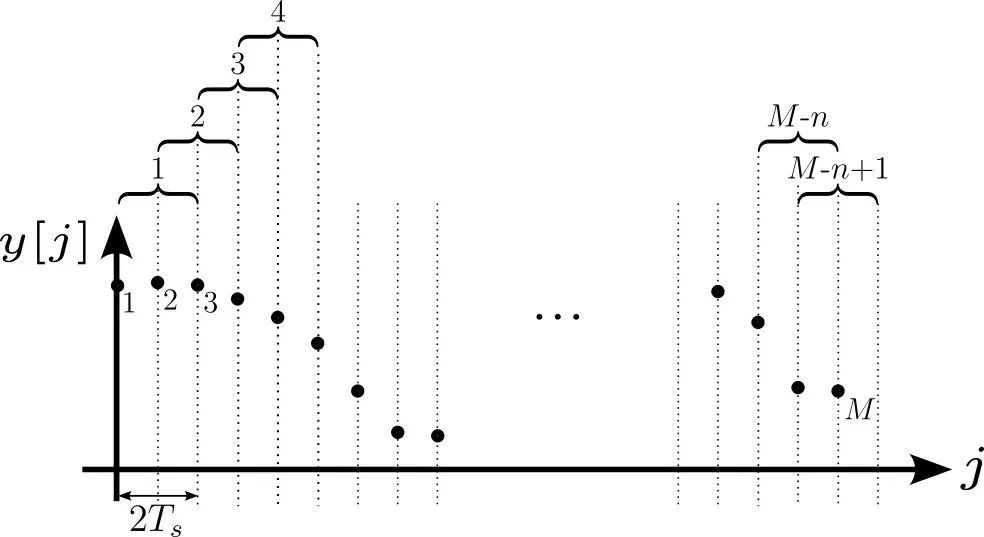
圖 4:為了最優化使用這些數據值,分段會重疊。這創建了額外的連續觀測時間對,所以增加了等式(3)中可能的被加數數量。在這個 n = 2 的案例中,受制于非重疊的分段,我們可以執行減法: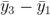 ,
,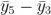 等等。現在我們還有:
等等。現在我們還有: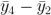 ,
,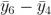 等等。盡管樣本并不完全獨立,但我們結果的可信度仍然有所提高。
等等。盡管樣本并不完全獨立,但我們結果的可信度仍然有所提高。
在這種情況下
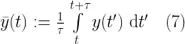
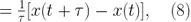
或者用離散函數表示,
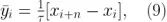
這樣等式(4)就變成
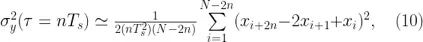
這里 N = M + 1 是 x 的長度。為了理清這一點,我們可以考慮 y 通過 x 的數值導數(差)來構造,因此 M = N ? 1。
這似乎像一個很抽象的簡化定義,當出于計算效率的原因,等式(10)提供了 Allan 方差最普遍的方程式。注意這里,x 測量值提供的是 y 的 Allan 方差,而非 x。
繪制Allan方差圖
Allan 方差通常針對多個平均時間進行運算,并且以 log - log 刻度繪圖(圖 5)。這樣的圖形有助于確定給定測量值的最佳平均時間。注意我們不會總是推薦使用較長的平均時間,特別是存在低頻漂移的情況下。
另外,常見的噪聲源一般以冪定律描述,它在 Allan 標準差圖上呈現已知的斜率。例如,白噪聲會隨著平均時間的平方根而減少。所以我們能夠預期白噪聲的斜率為 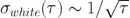 ,情況也確實如此。更普遍的是,如果特定噪聲源在功率譜密度 S 的斜率是
,情況也確實如此。更普遍的是,如果特定噪聲源在功率譜密度 S 的斜率是 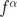 ,則Allan標準差的斜率即
,則Allan標準差的斜率即 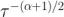 。
。
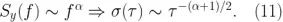
這一事實使人們能夠輕松確定哪個噪聲源在不同的平均時間內占主導地位,建立噪聲預度以確定系統性能是否得到充分理解,或量化每個誤差源的分布(圖 6)。
表1羅列了在研究時鐘和陀螺儀時常見噪聲源的斜率
表 1:針對選定應用中的不同噪聲源的斜率冪指數 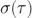 (即β是
(即β是 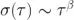 )[3, 5]。FM:頻率調制方式,PM:相位調制方式。
)[3, 5]。FM:頻率調制方式,PM:相位調制方式。

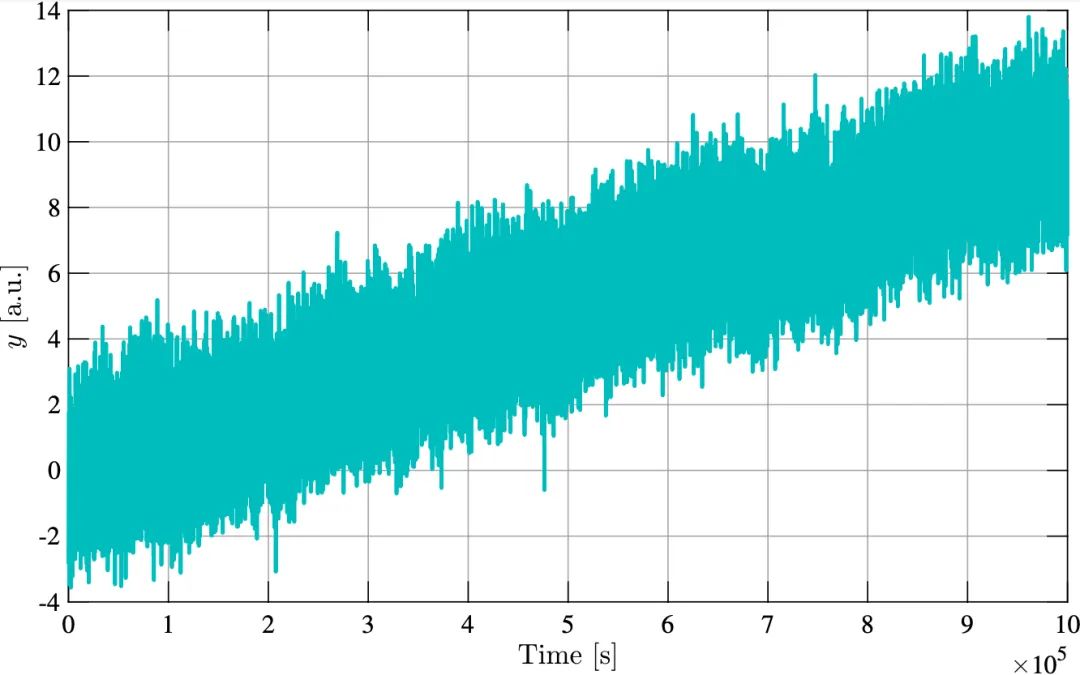
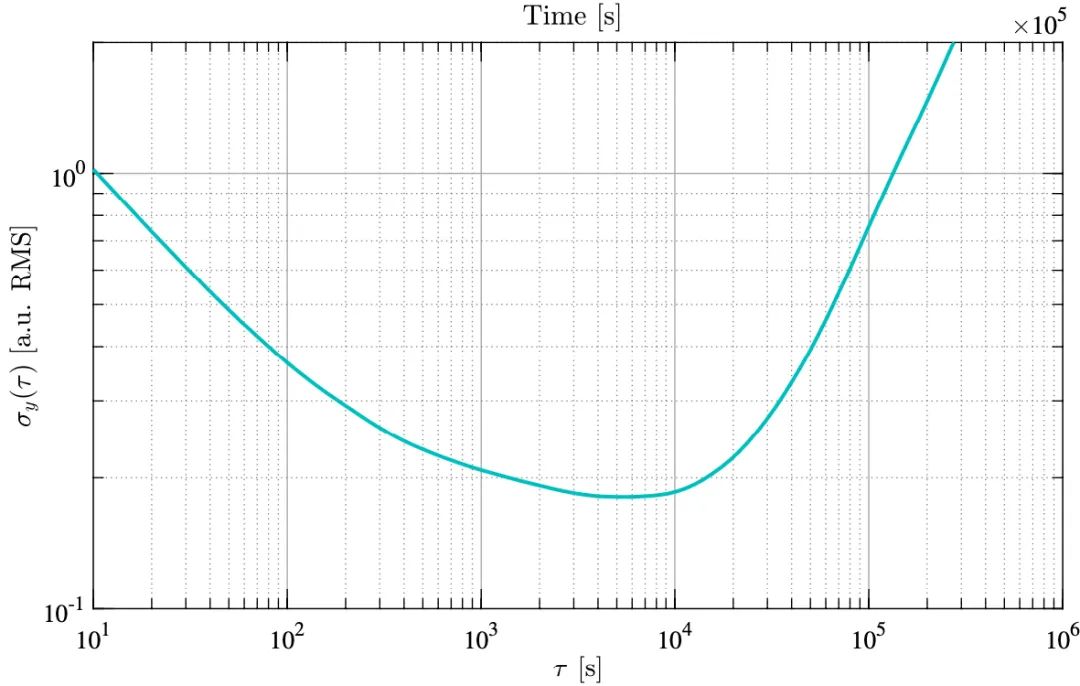
圖 5:時間序列(上軸)樣例,同時它相對應的 Allan 標準差圖(下軸)。 針對多個平均時間τ進行評估,結果以 log - log 刻度顯示。
針對多個平均時間τ進行評估,結果以 log - log 刻度顯示。
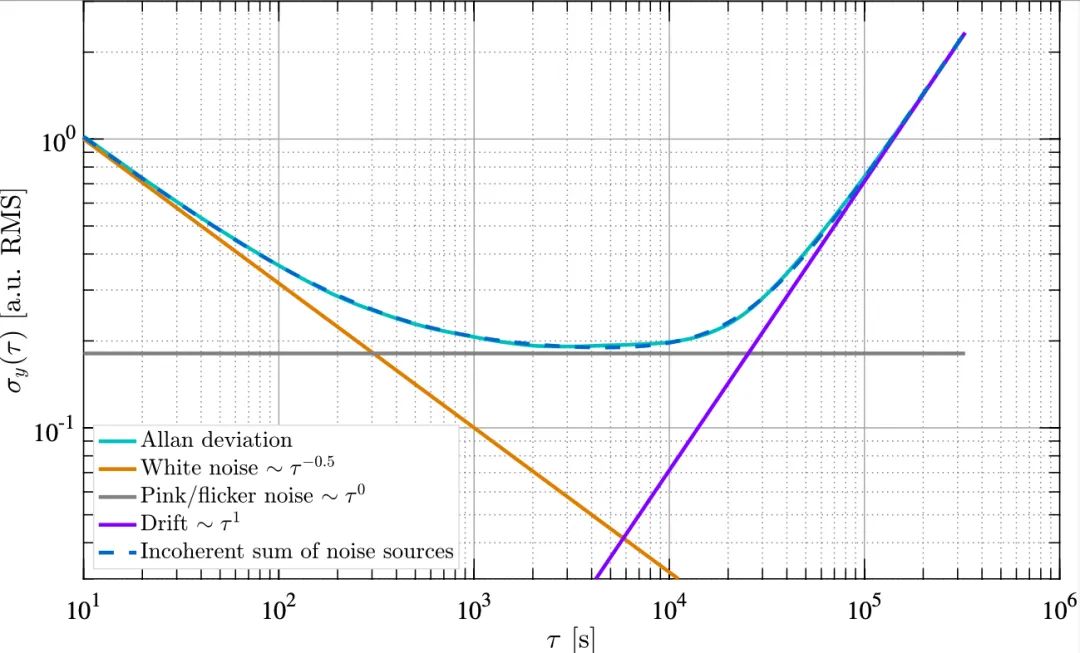
圖 6:冪定律噪聲源在 Allan 標準差圖上顯示為已知的斜率,讓我們可以容易地對系統噪聲建模。總的噪聲定義為不相干的獨立噪聲分布總和,即 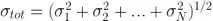 。在這種情況下,穩定性隨著平均時間的推移而提高(因為白噪聲的影響減少),直到粉紅/閃爍噪聲成為主導。在較長的時間尺度上,穩定性受到數據線性漂移的限制(參見圖 5,上軸)。當平均時間約為 5000秒時,測量結果最為穩定。
。在這種情況下,穩定性隨著平均時間的推移而提高(因為白噪聲的影響減少),直到粉紅/閃爍噪聲成為主導。在較長的時間尺度上,穩定性受到數據線性漂移的限制(參見圖 5,上軸)。當平均時間約為 5000秒時,測量結果最為穩定。
如何在Moku配置Allan方差測量
下方視頻演示如何在Moku配置Allan 方差測量。
功率譜密度vs Allan方差
就像我們前面提到的,有許多的工具可用于描述系統穩定性。雖然 Allan 方差是穩定性在時域上的計量,那功率譜密度(PSD),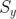 就是頻域上的對應項。如果 y 的單位是
就是頻域上的對應項。如果 y 的單位是 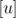 ,則
,則 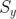 的單位是
的單位是 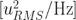 。當然在 Allan 方差中所包含的信息
。當然在 Allan 方差中所包含的信息 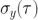 只是 PSD 中包含信息的替代表示,并且存在一個很接近的轉換形式(參考[6]中的附錄I)。注意這個只可以是從 PSD 向 Allan 方差的轉換,相反則不行。轉換方程如下:
只是 PSD 中包含信息的替代表示,并且存在一個很接近的轉換形式(參考[6]中的附錄I)。注意這個只可以是從 PSD 向 Allan 方差的轉換,相反則不行。轉換方程如下:
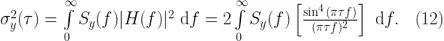
這里 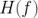 是時域采樣函數的傳遞函數。
是時域采樣函數的傳遞函數。
在這個情況下,我們需要注意一個有用的表達式:
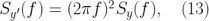
這里 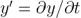 。我們可以以此為例,根據
。我們可以以此為例,根據 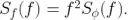 轉換 相位(φ)噪聲的 PSD 為頻率(f)噪聲之一。
轉換 相位(φ)噪聲的 PSD 為頻率(f)噪聲之一。
結果
我們在本文中已經介紹了 Allan 方差,展示如何計算并解釋分析。最初是在振蕩器穩定性的背景下開發的,目前仍是最常用的統計方法。不過 ,我們需要強調它適用于任何時間序列并且在廣泛的領域中大有用處。
Allan 方差有助于確定特定測量下的理想觀測時間并識別主要的噪聲源。還可以將功率譜密度轉換為阿倫方差。
Allan 方差是一種非常有用的統計工具,也是 Moku 相位表上可用于數據后續處理的眾多此類工具之一。其性能以及相位表的微弧度級精度和 Moku:app 的直觀用戶界面,使 Moku 成為在表征振蕩器系統穩定性的應用中卓越的設備。
除Allan方差之外
正如標準差存在局限性一樣,Allan 標準差也不是在所有情況下都是理想的統計方法。為了考慮完整,這里簡要討論了 Allan 標準差的兩種常用導數,它們在某些情況下提供了改善的性能。
修正Allan標準差
我們在上面注意到了在 Allan 標準差圖上(圖 6)基于梯度軌跡識別噪聲源的可能性。然而多個噪聲源會存在同一個斜率。特別是振蕩器白噪聲相位調制(WPM)和閃爍噪聲相位調制(FPM)會同時產生一個 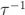 斜率(如表 1)。然而,WPM 對測量帶寬非常靈敏,FPM 則不然。通過在 n 個相鄰測量之間部署額外的平均方法,這里
斜率(如表 1)。然而,WPM 對測量帶寬非常靈敏,FPM 則不然。通過在 n 個相鄰測量之間部署額外的平均方法,這里 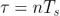 ,這樣修正后的 Allan 標準差,產生隨τ線性變窄的有效帶寬,同時能夠區分這些噪聲源[7]。
,這樣修正后的 Allan 標準差,產生隨τ線性變窄的有效帶寬,同時能夠區分這些噪聲源[7]。
修正的 Allan 標準差可以表示為:
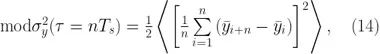
或者更實際一點,
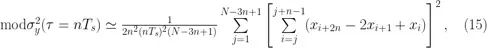
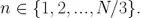
時間偏差
基于修正的Allan標準差更進一步的計量是時間偏差,或者時間Allan標準差 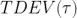 ,可以表示為:
,可以表示為:
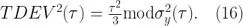
注意這不過是修正 Allan 方差的另一個版本(所有在 log - log 圖上的斜率通過τ的一次冪減少)。選擇歸一化因數使得當 n = 1 時,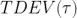 與白相位調制(PWM)噪聲保持一致。
與白相位調制(PWM)噪聲保持一致。
TDEV也經常用 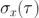 表示,明確了它是描述 x 穩定性(而不是 y)的事實。這是由于附加因子τ造成的。
表示,明確了它是描述 x 穩定性(而不是 y)的事實。這是由于附加因子τ造成的。
顧名思義,這種測量在表征時序分布信號非常有用,它用于描述時鐘的相位變化來作為平均時間的函數。
-
振蕩器
+關注
關注
28文章
3974瀏覽量
140561 -
測量
+關注
關注
10文章
5204瀏覽量
113063 -
Allan
+關注
關注
0文章
2瀏覽量
1142
發布評論請先 登錄
基于乘法器的模擬電路參數測量方法
PWM占空比的測量方法
概化理論的方差分量變異量的估計
捷聯慣導系統中Allan方差的使用要點
捷聯慣導系統中Allan方差的使用要點 分析
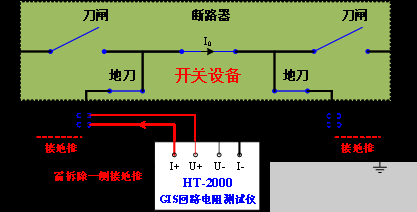
GIS回路電阻測量方法





 Allan 方差理論及測量方法
Allan 方差理論及測量方法












評論