BP(Backpropagation)神經(jīng)網(wǎng)絡(luò)是一種多層前饋神經(jīng)網(wǎng)絡(luò),其核心思想是通過(guò)反向傳播算法來(lái)調(diào)整網(wǎng)絡(luò)中的權(quán)重和偏置,從而實(shí)現(xiàn)對(duì)輸入數(shù)據(jù)的預(yù)測(cè)或分類。BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的建模是一個(gè)系統(tǒng)而復(fù)雜的過(guò)程,涉及數(shù)據(jù)預(yù)處理、網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計(jì)、權(quán)重初始化、前向傳播、損失函數(shù)計(jì)算、反向傳播、權(quán)重更新、模型評(píng)估與優(yōu)化等多個(gè)步驟。以下將詳細(xì)闡述這些步驟,并探討在建模過(guò)程中需要注意的關(guān)鍵點(diǎn)。
一、數(shù)據(jù)預(yù)處理
數(shù)據(jù)預(yù)處理是構(gòu)建BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的第一步,也是至關(guān)重要的一步。高質(zhì)量的數(shù)據(jù)是模型性能的基礎(chǔ),因此需要對(duì)原始數(shù)據(jù)進(jìn)行一系列的處理操作。
- 數(shù)據(jù)收集 :首先,需要收集足夠的數(shù)據(jù),這些數(shù)據(jù)可以是歷史數(shù)據(jù)、實(shí)驗(yàn)數(shù)據(jù)或模擬數(shù)據(jù)等。數(shù)據(jù)的質(zhì)量和數(shù)量直接影響模型的預(yù)測(cè)性能。
- 數(shù)據(jù)清洗 :去除數(shù)據(jù)中的噪聲、異常值和缺失值等,以保證數(shù)據(jù)的質(zhì)量和準(zhǔn)確性。常見的數(shù)據(jù)清洗方法包括填充缺失值(如使用均值、中位數(shù)或眾數(shù)填充)、去除異常值(如通過(guò)設(shè)定閾值或基于統(tǒng)計(jì)方法識(shí)別并刪除)、數(shù)據(jù)標(biāo)準(zhǔn)化(如歸一化或標(biāo)準(zhǔn)化處理)等。
- 特征選擇 :從原始數(shù)據(jù)中選擇對(duì)預(yù)測(cè)目標(biāo)有貢獻(xiàn)的特征,以減少模型的復(fù)雜度和提高預(yù)測(cè)性能。常見的特征選擇方法包括相關(guān)性分析、主成分分析(PCA)等。
- 數(shù)據(jù)集劃分 :將清洗和選擇后的數(shù)據(jù)集劃分為訓(xùn)練集、驗(yàn)證集和測(cè)試集。訓(xùn)練集用于訓(xùn)練模型,驗(yàn)證集用于調(diào)整模型參數(shù),測(cè)試集用于評(píng)估模型的預(yù)測(cè)性能。通常,訓(xùn)練集占總數(shù)據(jù)的70%-80%,驗(yàn)證集占10%-15%,測(cè)試集占10%-15%。
二、網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計(jì)
網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計(jì)是BP神經(jīng)網(wǎng)絡(luò)建模的核心環(huán)節(jié)之一,它決定了模型的復(fù)雜度和學(xué)習(xí)能力。
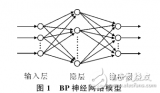
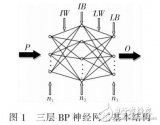
- 確定層數(shù) :BP神經(jīng)網(wǎng)絡(luò)至少包含三層:輸入層、一個(gè)或多個(gè)隱藏層以及輸出層。層數(shù)的選擇依賴于具體問(wèn)題的復(fù)雜度和數(shù)據(jù)量。一般來(lái)說(shuō),隱藏層的層數(shù)越多,模型的預(yù)測(cè)能力越強(qiáng),但同時(shí)模型的復(fù)雜度和訓(xùn)練時(shí)間也會(huì)增加。
- 確定節(jié)點(diǎn)數(shù) :
- 輸入層節(jié)點(diǎn)數(shù)應(yīng)與特征選擇后的特征數(shù)量相等。
- 隱藏層節(jié)點(diǎn)數(shù)的選擇沒有固定的規(guī)則,通常需要根據(jù)經(jīng)驗(yàn)或?qū)嶒?yàn)來(lái)確定。常用的經(jīng)驗(yàn)公式包括nh ? =ni ? +no??**+a,其中nh?是隱藏層節(jié)點(diǎn)數(shù),ni?是輸入層節(jié)點(diǎn)數(shù),no?**是輸出層節(jié)點(diǎn)數(shù),a是1到10之間的常數(shù)。
- 輸出層節(jié)點(diǎn)數(shù)應(yīng)與預(yù)測(cè)目標(biāo)的數(shù)量相等。例如,如果預(yù)測(cè)目標(biāo)是一個(gè)連續(xù)值,則輸出層節(jié)點(diǎn)數(shù)為1;如果預(yù)測(cè)目標(biāo)是一個(gè)分類問(wèn)題,輸出層節(jié)點(diǎn)數(shù)應(yīng)等于類別數(shù)。
- 選擇激活函數(shù) :激活函數(shù)用于引入非線性,使神經(jīng)網(wǎng)絡(luò)能夠擬合復(fù)雜的函數(shù)。常見的激活函數(shù)包括Sigmoid函數(shù)、Tanh函數(shù)、ReLU函數(shù)等。不同的激活函數(shù)對(duì)模型的預(yù)測(cè)性能和收斂速度有不同的影響,需要根據(jù)具體問(wèn)題進(jìn)行選擇。
三、權(quán)重初始化
在訓(xùn)練模型之前,需要為神經(jīng)網(wǎng)絡(luò)中的連接權(quán)重賦予初始值。權(quán)重初始化的好壞對(duì)模型的收斂速度和預(yù)測(cè)性能有很大影響。
- 隨機(jī)初始化 :使用小隨機(jī)數(shù)(如正態(tài)分布或均勻分布)來(lái)初始化權(quán)重。隨機(jī)初始化可以避免所有神經(jīng)元在訓(xùn)練初期具有相同的輸出,從而加速收斂。
- 特殊初始化方法 :如Xavier初始化和He初始化等,這些方法根據(jù)網(wǎng)絡(luò)結(jié)構(gòu)和激活函數(shù)的特點(diǎn)來(lái)設(shè)定初始權(quán)重,有助于改善模型的訓(xùn)練效果。
四、前向傳播
前向傳播是BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的基本操作之一,它描述了信息從輸入層通過(guò)隱藏層到輸出層的傳遞過(guò)程。
- 輸入數(shù)據(jù) :將訓(xùn)練集或測(cè)試集的輸入數(shù)據(jù)輸入到神經(jīng)網(wǎng)絡(luò)的輸入層。
- 逐層計(jì)算 :按照網(wǎng)絡(luò)結(jié)構(gòu)和權(quán)重,逐層計(jì)算每個(gè)神經(jīng)元的輸出值。在每個(gè)神經(jīng)元中,首先計(jì)算加權(quán)和(即將輸入數(shù)據(jù)與對(duì)應(yīng)的權(quán)重相乘并求和),然后應(yīng)用激活函數(shù)得到輸出值。
- 輸出結(jié)果 :最終得到輸出層的輸出值,即模型的預(yù)測(cè)結(jié)果。
五、損失函數(shù)計(jì)算
損失函數(shù)用于衡量模型預(yù)測(cè)值與實(shí)際值之間的差距,是優(yōu)化模型的關(guān)鍵指標(biāo)。
- 選擇損失函數(shù) :根據(jù)預(yù)測(cè)問(wèn)題的性質(zhì)選擇合適的損失函數(shù)。常見的損失函數(shù)包括均方誤差(MSE)和交叉熵?fù)p失等。均方誤差適用于回歸問(wèn)題,而交叉熵?fù)p失適用于分類問(wèn)題。
- 計(jì)算損失值 :根據(jù)模型預(yù)測(cè)值和實(shí)際值計(jì)算損失函數(shù)的值。損失值越小,表示模型的預(yù)測(cè)性能越好。### 六、反向傳播
反向傳播是BP神經(jīng)網(wǎng)絡(luò)的核心算法,它根據(jù)損失函數(shù)的梯度來(lái)調(diào)整網(wǎng)絡(luò)中的權(quán)重和偏置,以減小預(yù)測(cè)誤差。
- 計(jì)算梯度 :首先,從輸出層開始,根據(jù)損失函數(shù)的梯度,使用鏈?zhǔn)椒▌t逐層計(jì)算每個(gè)權(quán)重和偏置的梯度。這個(gè)過(guò)程中,激活函數(shù)的導(dǎo)數(shù)(如Sigmoid函數(shù)的導(dǎo)數(shù)、ReLU函數(shù)的導(dǎo)數(shù)等)起著關(guān)鍵作用。
- 梯度累積 :對(duì)于每個(gè)權(quán)重和偏置,將來(lái)自所有訓(xùn)練樣本的梯度進(jìn)行累積(或平均),以得到最終的梯度值。這一步是批量梯度下降(Batch Gradient Descent)或隨機(jī)梯度下降(Stochastic Gradient Descent, SGD)等優(yōu)化算法的基礎(chǔ)。
- 梯度裁剪 :為了避免梯度爆炸問(wèn)題,有時(shí)需要對(duì)梯度值進(jìn)行裁剪,即當(dāng)梯度值超過(guò)某個(gè)閾值時(shí),將其截?cái)酁樵撻撝怠?/li>
七、權(quán)重更新
根據(jù)計(jì)算得到的梯度,使用優(yōu)化算法來(lái)更新網(wǎng)絡(luò)中的權(quán)重和偏置。
- 選擇優(yōu)化算法 :常見的優(yōu)化算法包括梯度下降法(Gradient Descent)、動(dòng)量法(Momentum)、RMSprop、Adam等。這些算法各有優(yōu)缺點(diǎn),需要根據(jù)具體問(wèn)題和實(shí)驗(yàn)效果來(lái)選擇。
- 更新權(quán)重 :使用選定的優(yōu)化算法,根據(jù)梯度值更新每個(gè)權(quán)重和偏置。例如,在梯度下降法中,權(quán)重更新公式為 w = w ? η ? ? w ?L? ,其中w是權(quán)重,η是學(xué)習(xí)率,? w ?L?是權(quán)重的梯度。
八、迭代訓(xùn)練
通過(guò)反復(fù)進(jìn)行前向傳播、損失函數(shù)計(jì)算、反向傳播和權(quán)重更新這四個(gè)步驟,迭代訓(xùn)練BP神經(jīng)網(wǎng)絡(luò),直到滿足停止條件(如達(dá)到最大迭代次數(shù)、驗(yàn)證集損失不再下降等)。
- 監(jiān)控訓(xùn)練過(guò)程 :在訓(xùn)練過(guò)程中,需要監(jiān)控訓(xùn)練集和驗(yàn)證集的損失變化情況,以及模型的預(yù)測(cè)性能。這有助于及時(shí)發(fā)現(xiàn)過(guò)擬合或欠擬合等問(wèn)題,并采取相應(yīng)的措施進(jìn)行調(diào)整。
- 調(diào)整超參數(shù) :超參數(shù)包括學(xué)習(xí)率、批處理大小、隱藏層節(jié)點(diǎn)數(shù)、迭代次數(shù)等。在訓(xùn)練過(guò)程中,可能需要根據(jù)模型的表現(xiàn)調(diào)整這些超參數(shù),以獲得更好的預(yù)測(cè)性能。
九、模型評(píng)估與優(yōu)化
訓(xùn)練完成后,需要使用測(cè)試集對(duì)模型進(jìn)行評(píng)估,以驗(yàn)證其泛化能力。同時(shí),還可以根據(jù)評(píng)估結(jié)果對(duì)模型進(jìn)行進(jìn)一步的優(yōu)化。
- 評(píng)估模型 :使用測(cè)試集數(shù)據(jù)對(duì)模型進(jìn)行評(píng)估,計(jì)算預(yù)測(cè)準(zhǔn)確率、召回率、F1分?jǐn)?shù)等指標(biāo),以衡量模型的性能。
- 優(yōu)化模型 :根據(jù)評(píng)估結(jié)果,可以采取一系列措施來(lái)優(yōu)化模型。例如,調(diào)整網(wǎng)絡(luò)結(jié)構(gòu)、增加數(shù)據(jù)量、使用更復(fù)雜的特征、嘗試不同的優(yōu)化算法等。
- 模型解釋與可視化 :對(duì)于重要的應(yīng)用場(chǎng)景,還需要對(duì)模型進(jìn)行解釋和可視化,以便更好地理解模型的決策過(guò)程和預(yù)測(cè)結(jié)果。這有助于增強(qiáng)模型的透明度和可信度,并促進(jìn)模型的廣泛應(yīng)用。
十、結(jié)論與展望
BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的建模是一個(gè)復(fù)雜而系統(tǒng)的過(guò)程,涉及多個(gè)步驟和關(guān)鍵點(diǎn)的把握。通過(guò)精心設(shè)計(jì)網(wǎng)絡(luò)結(jié)構(gòu)、合理選擇超參數(shù)、迭代訓(xùn)練和優(yōu)化模型,可以構(gòu)建出性能優(yōu)良的預(yù)測(cè)模型,為實(shí)際問(wèn)題的解決提供有力支持。未來(lái),隨著深度學(xué)習(xí)技術(shù)的不斷發(fā)展,BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型將在更多領(lǐng)域發(fā)揮重要作用,為人類社會(huì)帶來(lái)更多便利和進(jìn)步。同時(shí),也需要不斷探索新的理論和方法,以應(yīng)對(duì)更加復(fù)雜和多樣化的預(yù)測(cè)問(wèn)題。
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4810瀏覽量
102900 -
BP神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
2文章
127瀏覽量
30877 -
預(yù)測(cè)模型
+關(guān)注
關(guān)注
0文章
27瀏覽量
8912
發(fā)布評(píng)論請(qǐng)先 登錄
用matlab編程進(jìn)行BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)時(shí)如何確定最合適的,BP模型
關(guān)于BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的確定!!
BP神經(jīng)網(wǎng)絡(luò)PID控制電機(jī)模型仿真
基于BP神經(jīng)網(wǎng)絡(luò)的PID控制
卷積神經(jīng)網(wǎng)絡(luò)模型發(fā)展及應(yīng)用
變壓器局放監(jiān)測(cè)與改進(jìn)BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型研究_高立慧
BP神經(jīng)網(wǎng)絡(luò)模型與學(xué)習(xí)算法
BP神經(jīng)網(wǎng)絡(luò)風(fēng)速預(yù)測(cè)方法
BP神經(jīng)網(wǎng)絡(luò)的稅收預(yù)測(cè)





 BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的建模步驟
BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型的建模步驟










評(píng)論