周立功教授新書《面向AMetal框架與接口的編程（上）》，對AMetal框架進行了詳細介紹，通過閱讀這本書，你可以學到高度復用的軟件設計原則和面向接口編程的開發思想，聚焦自己的“核心域”，改變自己的編程思維，實現企業和個人的共同進步。經周立功教授授權，即日起，致遠電子公眾號將對該書內容進行連載，愿共勉之。

本文為第三章：PWM 實現DAC 電路設計，內容包括：3.1 實現原理、3.2 電路設計、3.3 測試驗證、3.4 參數總結。

本章導讀：

當MCU 需要產生不同的模擬信號時，通常采用集成或獨立的D/A 轉換器實現。但是在要求低成本的場合，可以通過PWM 信號產生系統需要的直流和交流信號。

LPC824 內部有一個32 位PWM 定時器（SCTimer），它產生的PWM 信號搭配外圍電路可實現高分辨率、低成本的DAC，比如，12 位DAC。

3.1 實現原理

>>> 3.1.1 PWM 信號時域分析

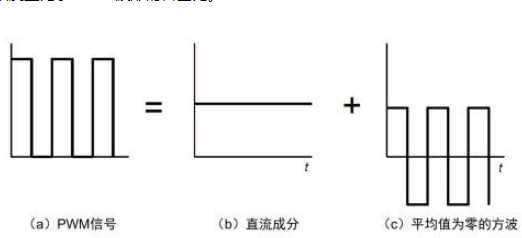
PWM（Pulse Width Modulation）是頻率固定、占空比變化的數字信號，PWM 信號波形可以被分解為一個直流分量加上一個相同占空比，但平均幅度為零的新的方波，詳見圖3.1，由此可見，這個直流分量的幅度正比于PWM 波形的占空比。

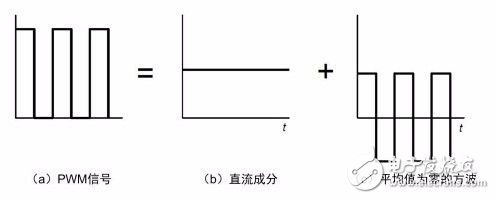
圖3.1 PWM 信號波形分解

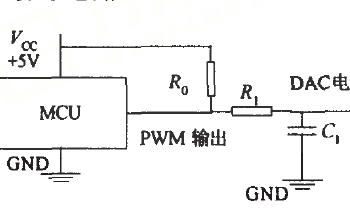
如果使PWM 信號的占空比隨時間改變，那么其直流分量隨之改變，信號濾除交流分量后將輸出幅度變化的模擬信號。因此通過改變PWM 信號的占空比，可以產生不同的模擬信號。這種技術稱之為PWM DAC，其原理可以形象地用圖3.2 表現出來。

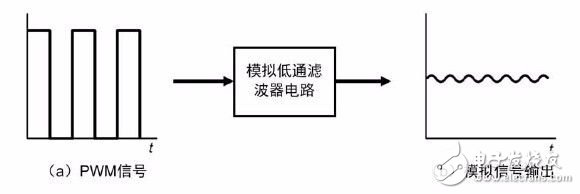
圖3.2 使用濾波器電路獲取PWM 的直流成分

>>> 3.1.2 PWM 信號頻域分析

從頻域分析進一步得到PWM 方式DAC的數學表達式。PWM 信號的函數波形詳見圖3.3，p 表示PWM 信號的占空比(0≤p≤1)，T表示載波周期。圖 3.3 是在不影響分析結果的前提下，移動函數波形的時間原點，使波形符合數學中的常規脈沖函數波形，以簡化數學分析。

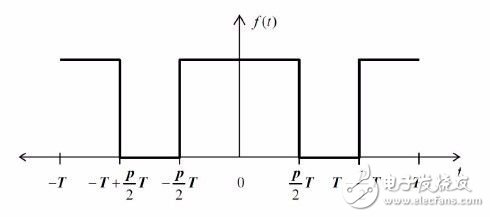
圖 3.3 PWM 信號函數波形

根據傅里葉理論，任意周期波形都可以分解為無限個頻率為其整數倍的諧波之和，周期函數f(t)的傅里葉級數展開結果如下：

如果令K 表示PWM 信號f(t)的幅度，代入公式(2)~(4)，f(t)的展開系數分別如下：

從展開式系數可以看到，直流分量A0 項等于PWM 波形幅度乘以PWM 波形占空比，這是所期望的D/A 轉換輸出結果。通過選擇合適的占空比，可以獲得0~K 之間的任意D/A轉換輸出電壓。

交流分量An 項是一系列頻率為PWM 信號載波頻率整數倍的高頻正弦諧波，對于D/A轉換轉換是不需要的成分。舉個例子，如果PWM 載波頻率為1MHz，那么交流分量將是1MHz、2MHz、3MHz 等等。此時經過一個截止頻率為1MHz 的理想低通濾波器，除去1MHz 及以上交流諧波，只剩下可任意設置直流分量，就是所期望的DAC 功能，DAC 表達式如下：

3.2 電路設計

PWM 實現DAC 的本質是需要保留直流分量去除交流分量，電路設計主要根據DAC 的分辨率，設計幅頻曲線陡峭的低通濾波器，將交流成分衰減至可接受的范圍內。對比無源RC、無源LC 低通濾波，由運放組成的有源低通濾波器，元件體積小，容易實現高階濾波器，并且低輸出阻抗，不存在帶負載能力問題，電路框圖詳見圖 3.4。

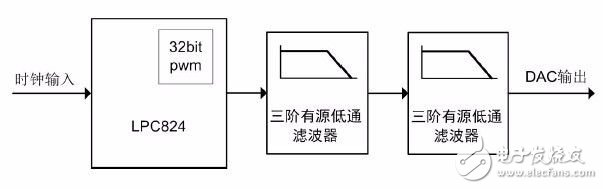
圖 3.4 PWM 實現DAC 電路框圖

該電路由兩個三階低通濾波器級聯形成六階低通濾波器，用于衰減LPC824 輸出PWM信號的高頻成分，實現12 位分辨率DAC。

>>> 3.2.1 DAC 分辨率

分辨率是DAC 的重要參數，存在兩個誤差源影響PWM 方式DAC 分辨率。首先，PWM信號的占空比只能表示有限的分辨率。在PWM 定時器最高時鐘固定的情況下，DAC 分辨率由PWM 信號載波頻率決定。例如，期望產生載波頻率100kHz 的PWM 信號，PWM 定時器時鐘為100MHz，這個時基在每個PWM 載波周期之中，最多提供1000 個計數值，通過指定PWM 定時器的比較值，最多提供1000 個PWM 占空比分辨率。

第二個誤差源是PWM 信號中不期望的諧波分量所產生的峰峰值紋波詳見圖 3.5，紋波峰值至少需小于1/2 個LSB，這兩個誤差源加在一起決定總的DAC 分辨率不確定性。

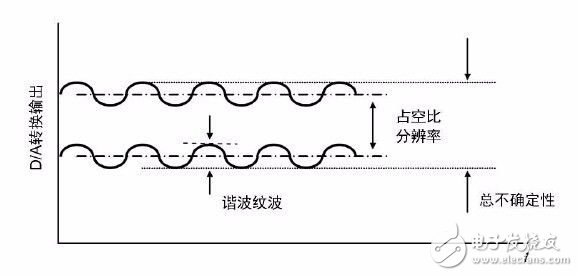
圖 3.5 影響PWM 方式DAC 分辨率的誤差源

改善第一個誤差源占空比分辨率，容易想到降低PWM 載波頻率。在前面例子中，將載波頻率由100kHz 降低至50kHz，對于100MHz 的時鐘，PWM 占空比分辨率增加至2000 個。然而，更低的載波頻率也降低了公式（6）中不期望諧波部分的基波頻率，一次諧波現在變為50kHz 而不是100kHz，如果硬件有源低通濾波器維持不變，其截止頻率不變，更多交流成分將穿過濾波器，諧波紋波峰值增加，會導致第二誤差源增加。

由此可見，根據確定的硬件濾波器來選擇PWM 載波頻率，在兩個誤差源PWM 占空比分辨率和諧波紋波之間存在矛盾。先確定載波頻率，再設計濾波器，是使得分辨率不確定性最小的方法。對于LPC824 的PWM 外設，設計12 位DAC 的計算步驟詳細介紹如下。

設定PWM 定時器時鐘。LPC824 運行時鐘高達30MHz，這里我們留出一些裕量，選擇10MHz 時鐘，周期為100ns。

設定PWM 信號載波頻率?？紤]將信號的周期設置為可以被4096 整除，這樣可以保證步進值為一個整數，保證轉換的準確性與簡便性。

因此PWM 的載波周期設定在409600ns，這樣在每次DAC 的數字代碼步進1 時，只需要將高電平持續時間加100ns，即步進一個計數值即可。我們可以輕松地算出PWM 的載波頻率為2.44KHz。

計算硬件低通濾波器所需的衰減倍數，PWM 信號的交流分量中，基波頻率最低，當占空比為50%時，基波的幅度最大，若這種情況下濾波器能將基波幅度衰減至1/2LSB 之下，則在所有占空比情況下，都可以將PWM 信號的交流分量衰減至1/2LSB 以下。因此可根據50%占空比時的基波幅度，計算所需的衰減倍數。

首先需要將n=1 代入公式（6），得到基波的幅度A_n=1：

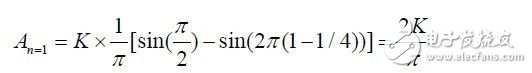
然后，計算使得基波幅度小于1/2LSB 的衰減倍數A_filter。

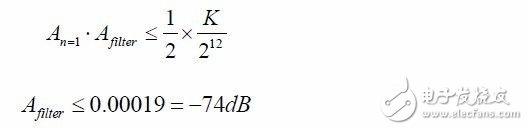
總結實現12 位DAC 分辨率的計算過程，LPC824 的PWM 時鐘設置為10MHz，載波頻率設置為2.44kHz，硬件低通濾波器需將2.44KHz 頻率分量衰減74dB 以上。

>>> 3.2.2 有源低通濾波器

在PWM 實現DAC 應用中，帶寬、阻帶滾降速率是兩個重要的濾波器性質。濾波器帶寬定義為幅頻響應等于0.707 倍時的頻率。濾波器帶寬直接揭示了最大信號帶寬，即PWM 方式DAC 能夠有效處理的最大信號頻率。阻帶滾降速率是高頻部分幅頻響應曲線的斜率。帶寬、滾降速率共同決定濾波器輸出端看到的諧波紋波幅度。

通常低通濾波器為-20dB 每十倍頻程每階濾波器，若低通濾波器帶寬設置為載波頻率的1/10 頻程，即0.244KHz，衰減-74dB 至少需4 階低通濾波器。綜合考慮帶寬、濾波器電路的復雜程度，低通濾波器帶寬設定在200Hz，使用兩級3 階巴特沃斯低通濾波器級聯形成6階濾波器，詳見圖 3.6。

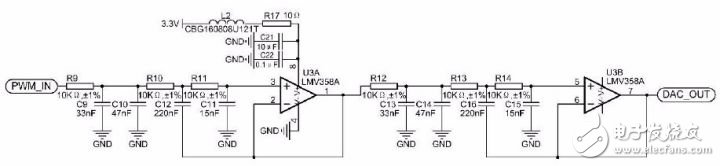
圖 3.6 6 階巴特沃斯有源低通濾波器電路

此濾波器電路的幅度曲線詳見圖 3.7，2.44kHz 頻率成分衰減比例為100dB 左右，具有足夠的裕量。如果只需用到10 位分辨率DAC，可只選擇使用第一級濾波器。

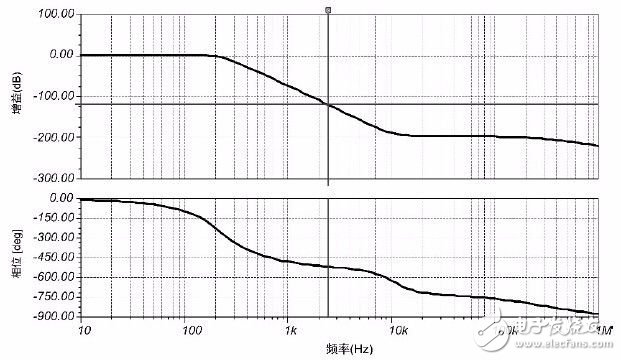
圖 3.7 6 階有源低通濾波器幅頻曲線

與LPC824 的ADC 信號輸入濾波器類似，這里再次使用單運放的三階濾波器電路拓撲，避免常規有源濾波器電路設計對運放的帶寬要求。常規配置需要運放增益帶寬積至少比輸入信號的最高頻率高5 到10 倍，否則當輸入信號的頻率成分高于增益帶寬時，高頻成分將直接饋通至輸出。根據PWM 信號的最小占空比100ns，主要高頻成分可達10MHz，需用到50M~100MHz 帶寬的精密運放。這類寬帶精密運放非常貴，有時相當于直接使用一個DAC芯片的成本。

而在圖 3.6 中，使用3peak 公司增益帶寬積僅為1MHz 的通用運放LMV358A 實現同樣功能，使得濾波器的成本可接受。

3.3 測試驗證

為驗證所實現12 位PWM DAC 的有效性，特制作了實際的電路板進行測試，主要測試數據為DNL、INL、建立時間。

>>> 3.3.1 DNL

DNL 差分非線性定義為任意兩個連續數字代碼所輸出步進電壓的實測值與理想值之差。理想DAC 的步進電壓為，每次嚴格步進一個LSB（DNL=0）。

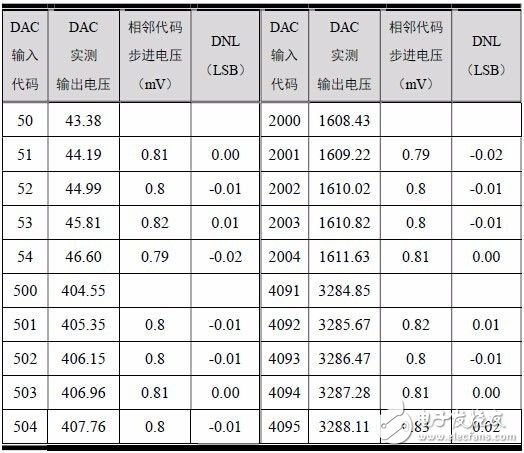
在DAC 輸入數字代碼范圍內，取若干點的DNL 測試驗證（1LSB=3.3V/2¹²=0.81mV），數據詳見表 3.1。可以看出，DNL 最大值為0.02 個LSB。

表 3.1 PWM DAC 的DNL 測試數據

>>> 3.3.2 INL

INL 積分非線性是表征DAC 精度的一個重要參數。在DAC 的全量程范圍內，設置輸入數字代碼從小至到大，依次等間距輸出一系列電壓值，可以線性擬合出一條最貼近這些電壓值的直線。理想情況下，DAC 是線性的，這些電壓值應該全部落在該直線上。實際輸出電壓值與擬合直線的偏離程度，則表征了DAC 的非線性。

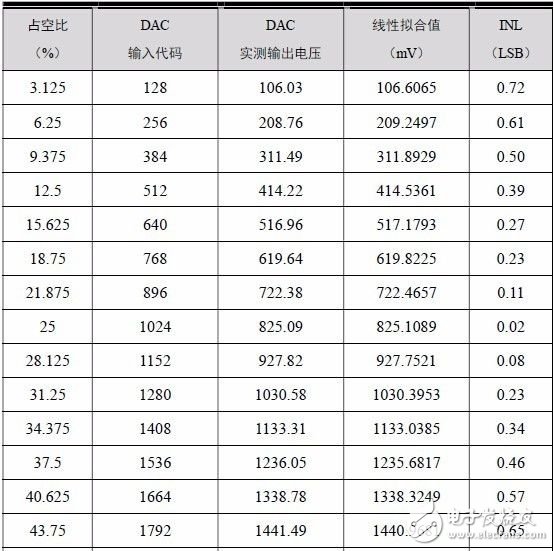
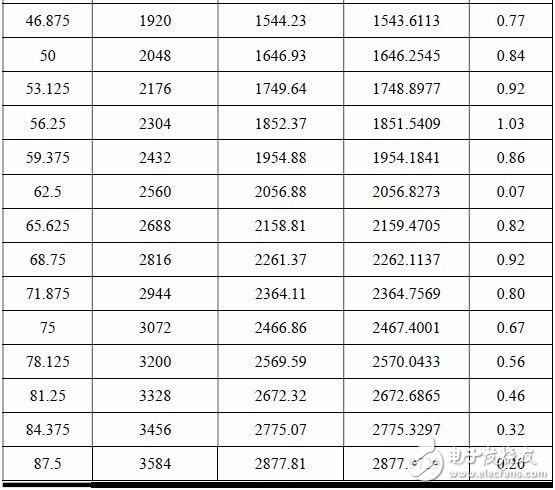
INL 測試數據詳見表 3.2，從表中數據可以看出，INL 最大值為1 個LSB。

表 3.2 PWM DAC 的INL 測試數據

>>> 3.3.3 建立時間

建立時間是指從發出更新輸出值的命令，到DAC 輸出電壓建立到最終值誤差范圍之內的時間間隔。建立時間受輸出有源低通濾波器的帶寬等參數影響，測試波形詳見圖 3.8。

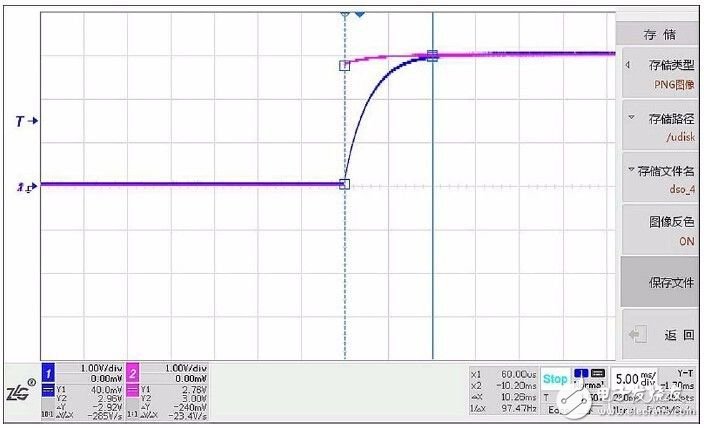
圖 3.8 PWM DAC 輸出建立時間測試

從上圖可以看出，建立時間ΔX 約為10ms。

3.4 參數總結

總結精度指標測試值詳見表 3.3，用作對比的AD5623 是常見的獨立12 位DAC 芯片。

表 3.3 PWM DAC 精度參數

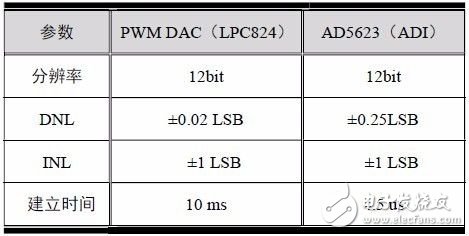
表中數據表明，LPC824 的PWM 外設結合本電路所實現DAC 有非常好的差分非線性（DNL）、線性度（INL），與獨立DAC 芯片基本一致。但建立時間慢，因此適合于輸出低頻、高精度的模擬信號。