最近我有一個同事老是問我“為什么我們用這么多激活函數？”，“為什么這個函數效果比那個好？”，“你怎么知道要用哪個函數？”，“這是很難的數學？”等等。所以我想，我何不給對神經網絡只有基本了解的人寫篇文章，介紹下激活函數和相應的數學呢？

注意：本文假設你對人工“神經元”有基本的了解。

激活函數

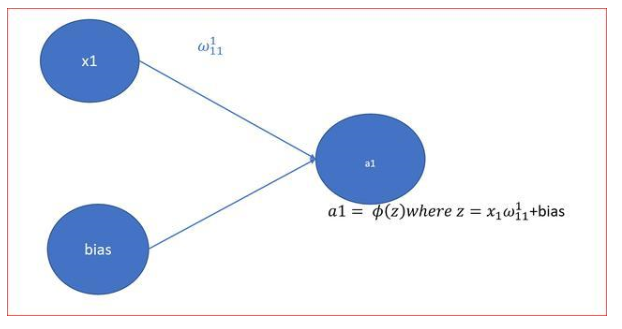
簡單來說，人工神經元計算輸入的“加權和”，加上偏置，接著決定是否需要“激活”（好吧，其實是激活函數決定是否激活，但是現在讓我們先這樣理解吧）。

考慮一個神經元。

上式中，Y的值可能是負無窮大到正無窮大之間的任意值。神經元并不知道值的界限。所以我們如何決定神經元是否需要激活呢？

為此，我們決定增加“激活函數”。

階躍函數

我們首先想到的是一個基于閾值的激活函數。如果Y的值大于一個特定值，就定義為“激活”。如果小于閾值，則不激活。

激活函數 A = “激活” if Y > 閾值 else not

或者，A = 1 if Y > 閾值, 否則 0

好吧，我們剛剛定義的是一個階躍函數（step function）。

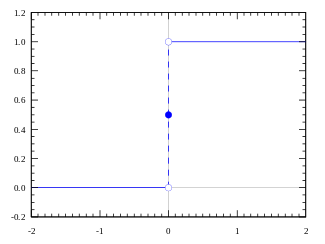
當值大于0（閾值）時，輸出為1（激活），否則輸出為0（不激活）。

很好。很清楚，這可以作為神經元的激活函數。然而，這個方法有一些特定的缺陷。

假設你正創建一個二元分類器，輸出“是”或“否”（激活或未激活）。一個階躍函數可以做到這一點。實際上這正是階躍函數做的事，輸出1或0。然后，想想如果你想要連接更多這樣的神經元來引入更多的分類，比如類一、類二、類三，等等。當不止一個神經元“激活”時會發生什么？所有的神經元將輸出1（基于階躍函數）。然后你如何決定最終結果屬于哪個分類呢？嗯，很難，很復雜。

你可能想要用當且僅當一個神經元輸出為1來表示分類結果。啊！這更難訓練了。更好的選擇是，激活函數不是二元的，可以表達“50%激活”、“20%激活”之類的概念。這樣，當不止一個神經元激活的時候，你可以找到“激活程度最高”的神經元（其實比max更優的選擇是softmax，不過目前我們就用max吧）。

當然，如果不止1個神經元表示“100%激活”了，問題仍然存在。不過，由于輸出存在中間值，因此學習過程將更平滑、更容易（較少波動），不止1個神經元100%激活的概率要比使用階躍函數訓練小很多（當然，這也取決于訓練的數據）。

好，所以我們希望輸出中間（模擬）激活值，而不是僅僅輸出“激活”或“不激活”（二元值）。

我們第一個想到的是線性函數。

線性函數

A = cx

以上是一個直線函數，激活與函數輸入（神經元的加權和）成比例。

所以這將給出一定范圍內的激活，而不是二元激活。我們當然可以連接若干神經元，如果不止一個神經元激活了，我們可以基于最大值（max或softmax）做決定。所以這很好。那么，這有什么問題呢？

如果你熟悉用于訓練的梯度下降，你會注意到這個函數的導數是一個常數。

A = cx對x的導數是c。這意味著梯度與x無關。這將是一個常數梯度。如果預測出現了錯誤，反向傳播進行的改動將是常數，而不依賴于輸入delta(x)！！！

這可不怎么好！（并非總是如此，但請容許我這么說。）此外，還有一個問題。想想連接起來的層。每個層由線性函數激活。這個激活接著作為下一層的輸入，下一層同樣基于線性函數激活，重復此過程，一直到最后一層。

不管我們有多少層，如果這些層的激活函數都是線性的，最后一層的最終激活函數將是第一層的輸入的線性函數！停頓一會，想想這個。

這意味著，這兩層（或N層）可以被一個單獨的層替換。啊！我們剛剛失去了堆疊網絡層的能力。不管我們堆疊多少層，整個網絡始終等價于帶線性激活的單層神經網絡（線性函數的線性組合仍然是一個線性函數）。

讓我們繼續吧。

sigmoid函數

好吧，這曲線看上去很平滑，有點像階躍函數。那這有什么好處呢？花點時間想一想。

首先，它是非線性的。這意味著該函數的組合也是非線性的。太棒了！我們可以堆疊網絡層了。至于非線性激活？是的，它是非線性激活！和階躍函數不同，它將給出模擬激活。同時，它也具備平滑的梯度。

不知道你注意到了沒有，當X位于-2和2之間時，Y的值非常陡峭。這意味著，此區間內X的任意微小變動都將導致Y顯著變動。這意味著，該函數趨向于將Y的值導向曲線的兩端。

看起來這個性質對分類器而言很有用？沒錯！確實是這樣。它趨向于將激活導向曲線的兩邊。這在預測上形成了清晰的差別。

另外一個優勢是，相對于線性函數(-inf, inf)的值域，該函數的值域為(0, 1)。因此我們的激活函數是有界的。

sigmoid函數是現在使用這廣泛的函數之一。那么，它有什么問題呢？

不知道你注意到了沒有，越是接近sigmoid的兩端，相對X的改變，Y就越趨向于作出非常小的反應。這意味著在該區域的梯度會很小。也就是“衰減的梯度”問題 。嗯，所以當激活函數接近曲線兩端的“鄰近地平線”部分時發生了什么？

梯度會很小，或者消失了（由于值極小，無法做出顯著的改變了）。網絡拒絕進一步學習，或者學習速度劇烈地變慢了（取決于具體案例，直到梯度/計算碰到了浮點值的限制）。不過，我們有一些變通措施，因此在分類問題中，sigmoid仍舊非常流行。

Tanh函數

另一個常用的激活函數是tanh函數。

嗯，這看起來和sigmoid很像嘛。實際上，這是一個經過拉升的sigmoid函數！

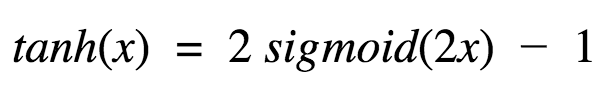
好，tanh的性質和我們之前討論的sigmoid類似。它是非線性的，因此我們可以堆疊網絡層。它是有界的(-1, 1)，所以不用擔心激活膨脹。值得一提的是，tanh的梯度比sigmoid更激烈（導數更陡峭）。因此，選擇sigmoid還是tanh將取決于你對梯度強度的需求。和sigmoid類似，tanh也存在梯度衰減問題。

tanh也是一個非常流行和廣泛使用的激活函數。

ReLu

接著，是ReLu函數，

A(x) = max(0, x)

ReLu函數如上所示。當x是正值時，它輸出x，否則輸出0。

乍看起來這和線性函數有一樣的問題，因為在正值處它是線性的。首先，RuLu是非線性的。ReLu的組合也是非線性的！（實際上它是一個很好的逼近子。ReLu的組合可以逼近任何函數。）很好，這意味著我們可以堆疊網絡層。不過，它并不是有界的。ReLu的值域是[0, inf)。這意味著它將膨脹激活函數。

我想指出的另一點是激活的稀疏性。想象一個具有很多神經元的大型神經網絡。使用sigmoid或tanh會導致幾乎所有神經元以模擬的方式激活（沒忘吧？）這意味著需要處理幾乎所有的激活以描述網絡的輸出。換句話說，激活是密集的。這樣成本很高。理想情況下，我們希望網絡中的一些神經元不激活，從而使激活變得稀疏和高效。

ReLu在這方面很有用。想象一個具備隨機初始權重（或歸一化的權重）的網絡，基于ReLu的特性（x的負值將輸出0），基本上50%的網絡將生成0。這意味著更少的神經元將被激活（稀疏激活），網絡也更輕量。哇，棒！ReLu看起來真不錯！是的，它確實不錯，但沒什么東西不存在缺陷……甚至是RuLu。

ReLu的水平線部分（X的負值）意味著梯度會趨向于0。當激活位于ReLu的水平區域時，梯度會是0，導致權重無法隨著梯度而調整。這意味著，陷入此狀態的神經元將停止對誤差/輸入作出反應（很簡單，因為梯度是0，沒有什么改變）。這被稱為死亡ReLu問題。這一問題會導致一些神經元直接死亡、失去響應，導致網絡的很大一部分進入被動狀態。有一些緩和這一問題的ReLu變體，將水平線轉為非水平部分，例如，當x<0時y = 0.01x，使圖像從水平線變為略微傾斜的直線。這就是弱修正ReLu（leaky ReLu）。還有其他一些變體。主要的想法是讓梯度不為零，這樣網絡可以逐漸從訓練中恢復。

相比tanh和sigmoid，ReLu在算力上更經濟，因為它使用的是比較簡單的數學運算。設計深度神經網絡的時候，這是需要考慮的一個重要因素。

好，該選哪個呢？

現在來考慮該用哪個激活函數的問題。我們是否應該總是使用ReLu呢？還是sigmoid或tanh？好，是也不是。當我們知道嘗試逼近的函數具有某些特定性質時，我們可以選擇能夠更快逼近函數的激活函數，從而加快訓練過程。例如，sigmoid對分類器而言很有效（看看sigmoid的圖像，是不是展示了一個理想的分類器的性質？），因為基于sigmoid的組合逼近的分類函數要比諸如ReLu之類的函數更容易。當然，你也可以使用自己定制的函數！如果你并不清楚試圖學習的函數的本質，那我會建議你從ReLu開始，然后再試其他。在大多數情況下，ReLu作為一個通用的逼近子效果很不錯。

在本文中，我嘗試描述了一些常用的激活函數。還有其他的激活函數，但基本的思想是一樣的。尋找更好的激活函數的研究仍在進行。希望你理解了激活函數背后的思想，為什么要使用激活函數，以及如何選用激活函數。