ADC 是什么？我們為什么需要 ADC？ADC 有哪些架構？他們的工作原理和特點是什么，分別適用于哪些場景？今天，就讓 MPS 的 ADC 資深工程師為您逐一解密！

文末匯總了 ADC 五大架構的速度、精度和應用場景對比，如此實用又貼心？火速收藏！

一、ADC 是什么？

ADC 的英文全拼是 Analog to Digital Converter，中文為模數轉換器，它可以將連續模擬輸入信號轉換為離散的數字信號，并以一序列 1 和 0 的形式進行傳送。這些輸入信號被量化為數字量后，再進行傳輸或進一步后續處理時，就不易受噪聲干擾。

模擬信號：連續變化的物理量所表達的信息，如溫度、濕度、壓力、長度、電流、電壓、光強、音色等。

數字信號：自變量和因變量都是離散的數據信息，通常容易被 MCU/DSP/CPU 進行后續處理的二進制數來表達。

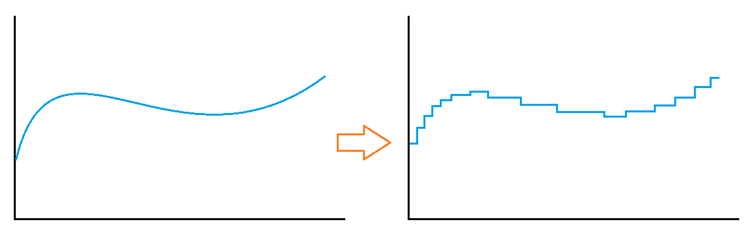
從模擬到數字的變換就像從真實世界進入到像素世界，我們日常生活中常講到的數碼相機、手機上的攝像頭模組內，就包含一個成像專用的 ADC，將圖像中每個像素單元的模擬光強度值轉換成數字量。

二、我們為什么需要 ADC？

現實世界中，我們被溫度、濕度、光、聲等物理量包圍，作為有著感知能力的生物體，我們能夠非常自然地獲取模擬信號，并與這些物理量達成默契，但是對于 CPU、MCU 等各類電子設備來說，這些信號卻很難被理解。

在數字化社會中，一切事物都被賦予了可量化的期待，對數據的讀取、處理、傳輸和存儲，成為了人類認識事物的基本邏輯。

因此，我們需要將現實世界中的模擬信號轉換為機器能夠理解的數字表達。現實世界和數字世界的“窗戶紙”將由模數轉換器（ADC）來捅破。

三、ADC 有哪些架構？工作原理是什么？

ADC 架構有：并行比較型（Flash），逐次逼近型（Successive Approximation Register），積分型（Integrating），增量型（Delta-Sigma），流水線型（Pipeline）等。

1 并行比較型（Flash）

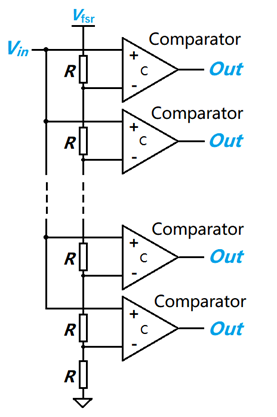
下圖是并行比較型 ADC 的拓撲原理圖，采樣輸入信號和設置好的比較電平直接比較得到輸出。

下圖中假設有 n 個比較器，最下面的是第 1 個，滿量程輸入電平是 Vfsr，作為參考電壓，由 n+1 個等值電阻將其均分為 n 個階梯，那么第 X 個比較器負向輸入電壓為 Vfsr·X/(n+1)，如果從第 m 個比較器開始以上的比較器輸出都是 0，以下的輸出都是 1，那么輸入信號電壓為：

Vin = Vfsr · m/(n+1)

2 逐次逼近型（SAR）

一個 n 位分辨率的 SAR 型 ADC，第一階段，輸入信號先和設定好的比較電平輸入比較器作比較，比較電平設置為 ADC 滿量程的一半 Vfsr·2-1，輸出第一位二進制結果 B1，將 B1 存入寄存器，第二階段，輸入比較器的比較電平根據第一次的比較結果設置為 Vfsr·2-1+(2·B1-1)Vfsr·2-2，此處的B1及后面公式中的B2,B3,Bn-1,Bn均作為十進制數參與計算，比較后輸出第二位結果 B2，同樣存入寄存器，進入第三階段，比較電平設置為 Vfsr·2-1+(2·B1-1)Vfsr·2-2+(2·B2-1)Vfsr·2-3，得到第三位結果 B3，直至第 n 階段，比較電平設置為 Vfsr·2-1+(2·B1-1)Vfsr·2-2+(2·B2-1)Vfsr·2-3+…+(2·Bn-1-1)Vfsr·2-n，得到最后一位結果 Bn，由最高位 B1 至最低位 Bn 組成的 n 位二進制數即為該 n 位 ADC 的輸出結果，轉化為 10 進制數 D，那輸入信號的電平測量值等于 Vfsr·D·2-n。

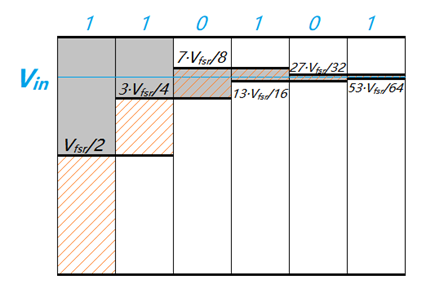
例如下圖是一個 6bit 的 SAR 型 ADC 的轉化流程，輸入信號先和 Vfsr/2 比較得到最高位 1，之后再和 Vfsr/2+Vfsr/4 比較得到第二位 1，繼續下去，得到二進制結果 110101，根據上文的公式 Vfsr·D·2-n 得出輸入電平為 53·Vfsr/64，理論誤差小于 Vfsr/64。

3積分型（Integrating）

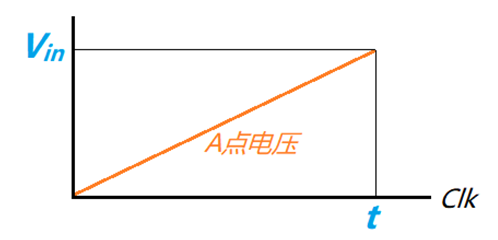
下圖是單斜率積分型 ADC 的拓撲原理圖，通過積分器從 0 電平積分到達采樣信號電平的時間計算得到采樣電平。

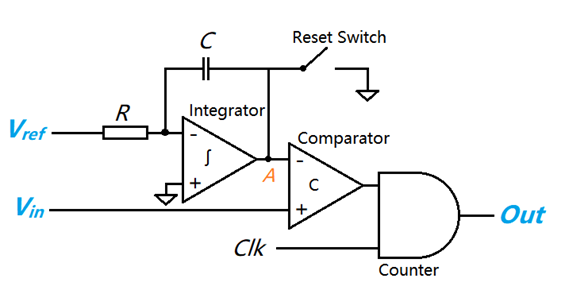
采樣開始時，積分器開始積分，同時計數器開始對輸入的時鐘信號 Clk 計數，假設該時鐘頻率為 f，積分電流為 Vref/R，經過時間 t 后 A 點電壓超過輸入信號的電壓值，比較器輸出從 1 跳變至 0，計數器停止計數，得到計數值 k，通過下方公式計算得到輸入電壓。

Vin = (Vref/R)·k/(C·f)

另外還有雙斜率積分型 ADC，分時將輸入電平和參考電平分別做正向和反向積分，可以更好的消除積分電路帶來的誤差，但是會增加一次積分時間，轉換速度會更慢。

4增量型（Delta-Sigma）

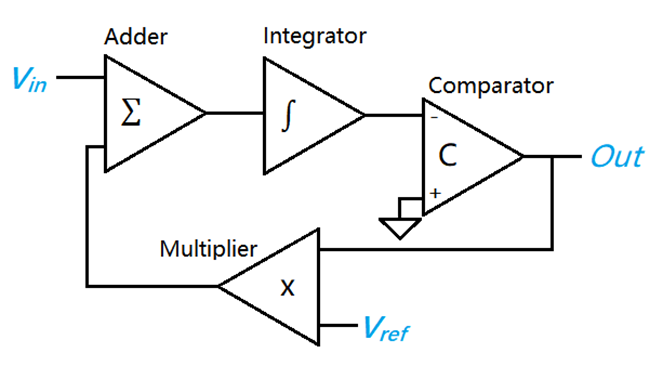
增量型 ADC 的拓撲原理圖如下，先看積分器，如果輸出小于 0，比較器輸出 1，否則輸出 -1，比較器輸出 1 時，乘法器輸出 Vref，否則輸出 -Vref，所以當積分器輸出大于 0 時，將有 Vin-Vref輸入到積分器中進行下一次比較，否則輸入 Vin+Vref，記錄每一次比較器的輸出，統計輸出 -1 的次數 X 和總比較次數 m，通過下方公式來計算輸入電平，總的比較次數越高，分辨率越高。

Vin = Vref·(2·X-m)/m

5流水線型（Pipeline）

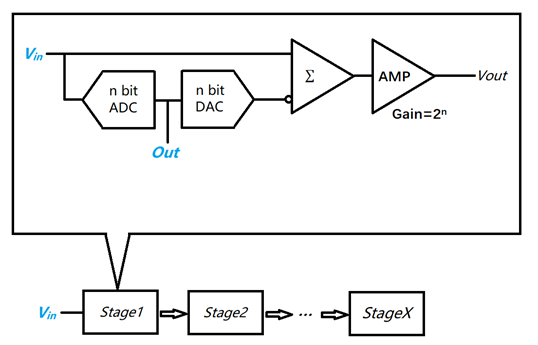
流水線型 ADC 通常由多個相同結構的子單元組成，每個子單元包含一個 ADC，一個反向DAC，一個減法器，一個固定增益的放大器構成，子單元中的 ADC 多為 Flash 型，也有 SAR 型。

如下圖，假如一個 X 階的理想化流水線 ADC，子單元中的 ADC 的精度為 n bit，該子單元滿量程為 Vfsr，假設該子單元 m 輸入信號 Vin 被該子單元內 ADC 量化的結果為 Am·Vfsr，那么該單元可輸出的結果最小值 Amin=0，最大值 Amax=(2-n-1)/2n，將 Vin 和該量化結果通過 DAC 轉化為模擬信號后送入減法器會得到一個小于等于 Vfsr·2--n 的差值 Vin-Am·Vfsr，該差值通過子單元內增益為 2n 的放大器放大后得到電平為 2n·(Vin-Am·Vfsr) 的模擬信號輸出該單元，再作為輸入進入下一級子單元 m+1，經過同樣的流程得到量化結果 Am+1·Vfsr，每一級將輸入信號和量化信號的差值放大后送至下一級再做量化，經過 X 階最終會產生一個 X·n 位精度的量化結果，由以下公式計算，

Vin= Vfsr·(A1+A2·2-n+A3·2-2n+…+AX·2-(X-1)n)

以上是理想狀態，而實際情況是前級 ADC 的失調誤差會導致輸入信號和 DAC 輸出的差值超出 0 到 Vfsr·2--n 的范圍，此時 2-n 的增益會導致輸入到下一級的信號超出量程范圍，為解決這個問題一般的做法是將放大器的增益降為 2-n-1，利用后一級的冗余測量范圍來校正上一級的誤差。

每一級在完成當前流程后新的信號便可以輸入進行新的量化，因此平均轉換時間僅相當于信號走完單個子單元的時間 t，所以平均轉換速度會很快，但是每個信號需要通過所有級才可以得到最終結果，因此當一個信號輸入到得到結果至少需要時間 Xt，因此流水線型 ADC 是一種轉換快，但是高精度的會有較高的延遲。

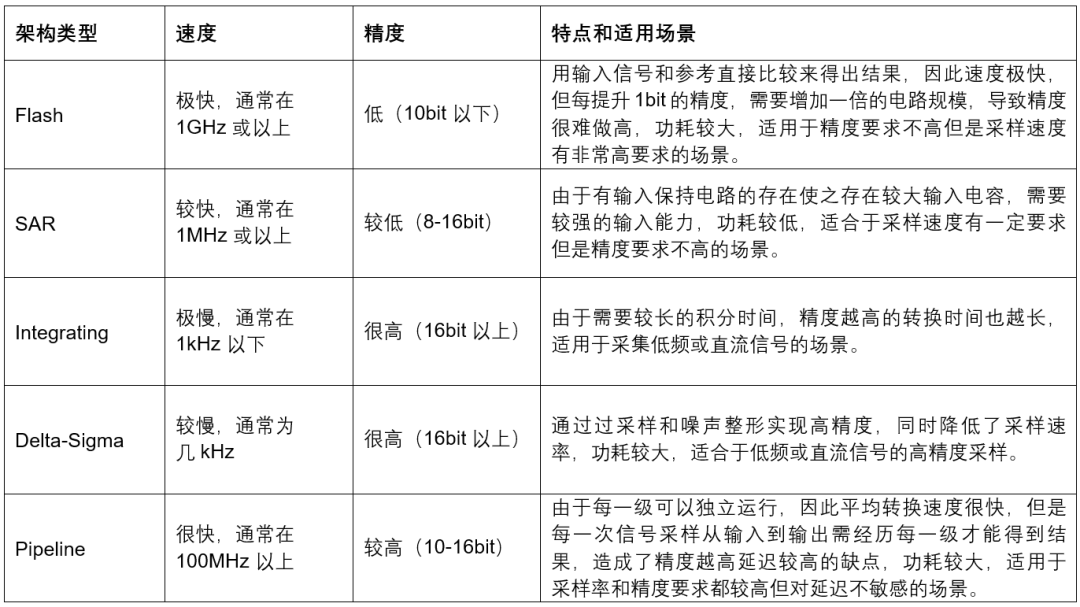
四、ADC 五大架構對比