“什么是 Vrms ？ 如何推導(dǎo)正弦波的 RMS 值？ ”

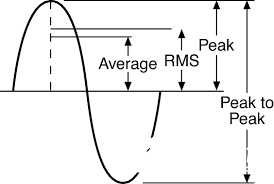
熟悉我的讀者都知道，在電子技術(shù)類文章中，我始終避免預(yù)設(shè)讀者具備微積分基礎(chǔ)。我始終認(rèn)為，即使在極客群體中，真正精通微積分的人也是鳳毛麟角。許多大學(xué)的微積分課程充斥著填鴨式教學(xué)——那些解釋不清的公式需要耗費(fèi)大量時(shí)間死記硬背，卻只需轉(zhuǎn)瞬就能忘得干干凈凈。雖然某些推導(dǎo)確實(shí)無(wú)法繞開(kāi)數(shù)學(xué)工具，但在絕大多數(shù)情況下，電氣工程類文章對(duì)微積分的依賴根本毫無(wú)必要。

今天，我要針對(duì)當(dāng)前谷歌搜索排名第一的均方根電壓（Vrms）公式推導(dǎo)方法提出尖銳批評(píng)。這個(gè)推導(dǎo)過(guò)程充斥著以下問(wèn)題：

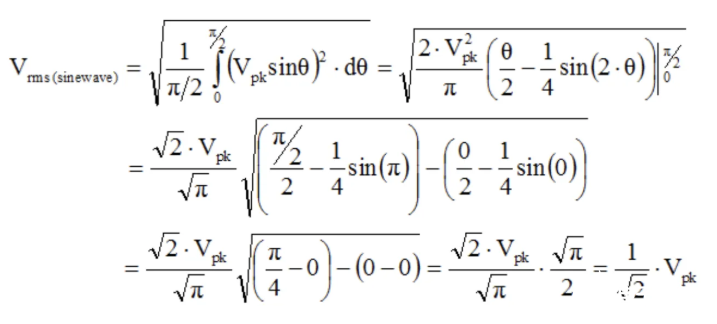? 到底什么是 Vrms? 在電路設(shè)計(jì)中，常需計(jì)算已知電阻上隨時(shí)間變化的電壓信號(hào)所消耗的功率。例如，設(shè)計(jì)驅(qū)動(dòng)音響的功放電路時(shí)，需確保功率不超過(guò)揚(yáng)聲器線圈的額定值（以瓦特為單位）。現(xiàn)代功放多以電壓信號(hào)驅(qū)動(dòng)，而揚(yáng)聲器阻抗固定，因此需建立電壓與功率的等效關(guān)系。

計(jì)算功率的公式為：

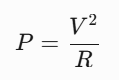
如果電壓是恒定的，這個(gè)公式?jīng)]有問(wèn)題，但如果信號(hào)隨時(shí)間變化呢？

為了回答該問(wèn)題，我們以一個(gè)10Ω負(fù)載和分三個(gè)離散階躍變化（1V、10V，再回到1V）的電源電壓構(gòu)成的簡(jiǎn)化示例進(jìn)行分析。在這種設(shè)置中，每個(gè)時(shí)間段本質(zhì)上都是獨(dú)立的‘穩(wěn)態(tài)’情景，因此可以相應(yīng)地拆分計(jì)算步驟：

這樣，我們就可以計(jì)算出一個(gè)簡(jiǎn)單的算術(shù)平均值，從而得到負(fù)載在一段時(shí)間內(nèi)的平均耗散功率：

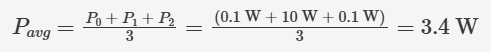
該結(jié)果雖然正確，但這種計(jì)算方式并不總是便捷。例如，當(dāng)涉及超過(guò)三個(gè)電壓等級(jí)時(shí)，針對(duì)不同音量旋鈕位置重新計(jì)算總和將十分繁瑣。若我們能找到一個(gè)等效直流電壓，使其在負(fù)載上消耗的功率與待研究的交流信號(hào)相同，便能以更直接的方式建模音量與功率的關(guān)系。

然而如何計(jì)算該等效電壓？是否僅對(duì)各時(shí)間段電壓取算術(shù)平均值？讓我們深入探究：

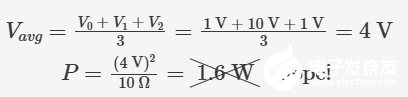? 結(jié)果并不一致。問(wèn)題出在功率方程中的 V2 項(xiàng)。為了找出正確的方法，我們可以用符號(hào)來(lái)求解示例中的功率方程。

組成方程為 P0 = V0 / R、P1 = V1 / R 和 P3 = V3 / R，因此：

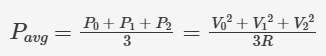
換一種描述方式：

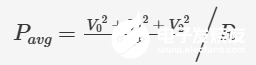
該表達(dá)式的前半部分正是電壓平方的算術(shù)平均值，恰好占據(jù)原恒壓公式中 V2 的位置！換言之，我們先將原始波形進(jìn)行平方運(yùn)算，然后計(jì)算其標(biāo)準(zhǔn)算術(shù)平均值。

無(wú)論如何，我們暫且將這個(gè)特殊平均值稱為x，并驗(yàn)證其數(shù)學(xué)合理性：

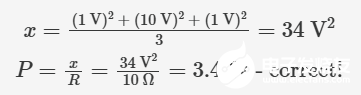
但從物理意義上說(shuō)，x 究竟代表什么？它并不能代替原始功率表達(dá)式中的電壓；請(qǐng)記住，它取代的是電壓的平方 (V2)。要得到我們說(shuō)過(guò)的功率等效電壓，我們需要計(jì)算這個(gè)值的平方根。

而這正是‘均方根電壓’（Vrms）的定義：它是波形平方（S）的算術(shù)平均值（M）的平方根（R）。本例中，Vrms = √34 ≈ 5.831 V。我們只需將 Vrms 除以二，即可模擬輸入信號(hào)振幅減半對(duì)耗散功率的影響。

方波在兩個(gè)電壓（Vlo和 Vhi）之間交替變化的情況與本節(jié)前面討論的方法類似，只是我們只需要計(jì)算兩個(gè)點(diǎn)的平均值，而不是三個(gè)點(diǎn)的平均值：

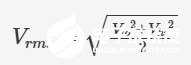
但對(duì)于連續(xù)變化的信號(hào)該如何處理？

正弦函數(shù)的 Vrms

在模擬電子領(lǐng)域，我們常需處理正弦信號(hào)--此時(shí)維基百科通常會(huì)引入微積分進(jìn)行推導(dǎo)。但我們能否避開(kāi)復(fù)雜的積分運(yùn)算？

答案是可以！回顧可知，計(jì)算任意波形的均方根值（RMS），需對(duì)波形進(jìn)行平方（S）、取算術(shù)平均（M）、再開(kāi)平方根（R）三步操作。

我們可以先將波形平方。給定峰值振幅 Vp 的正弦波信號(hào)的一般方程如下：

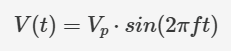
將右側(cè)平方后得到：

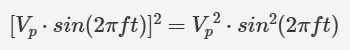
表達(dá)式中唯一隨時(shí)間變化的部分是 sin2(...) 函數(shù)。讓我們使用一個(gè)新符號(hào) Sm 來(lái)表示其平均值。這樣，我們就可以用下面的方式寫(xiě)出 Vrms 表達(dá)式：

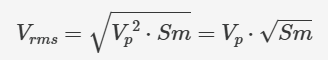
現(xiàn)在，我們要做的就是找出 Sm。要找到任何周期性波形的平均值，我們只需考慮一個(gè)周期；任何重復(fù)序列的平均值都與單個(gè)周期的平均值相同：

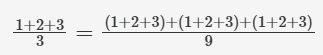
在計(jì)算sin2(...)的周期時(shí)，必須與平方前的正弦函數(shù)周期對(duì)齊，即參數(shù)范圍應(yīng)限定在0°至360°之間。但即便如此，我們?nèi)孕鑼?duì)無(wú)限個(gè)連續(xù)變化的值進(jìn)行平均運(yùn)算！

幸運(yùn)的是，三角函數(shù)提供了解決方案。讓我們拋開(kāi)具體的 Vrms 情景，考慮一個(gè)由常規(guī)三角函數(shù)描述的臨時(shí)構(gòu)建的直角三角形：

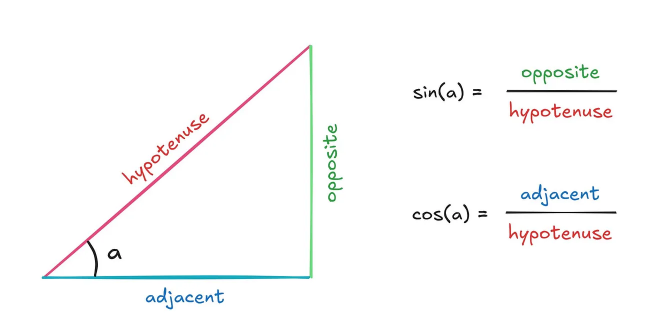
假設(shè)我們知道斜邊的長(zhǎng)度--稱之為 n--并知道角度 a。很明顯，垂直邊的高等于 sin(a) ×n，水平邊的長(zhǎng)度等于 cos(a) ×n。

這是一個(gè)直角三角形，我們還可以用勾股定理來(lái)描述它的邊之間的關(guān)系：斜邊的平方等于對(duì)邊的平方加鄰邊的平方。

我們已經(jīng)知道了這些邊的值，斜邊是 n，其他邊由角度 a 的三角函數(shù)給出：

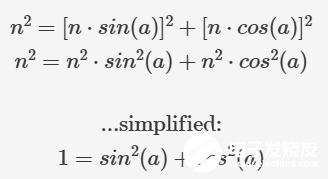
這一普適性法則揭示了正弦平方與余弦平方之間的奇妙關(guān)系，被稱為畢達(dá)哥拉斯恒等式。

現(xiàn)在，讓我們回到 RMS 的難題上。為了解釋下一步，想象一下你只在儲(chǔ)蓄罐里放 5 美元的鈔票，那么儲(chǔ)蓄罐里鈔票的平均值必然是 5 美元。同樣，如果存在這樣一個(gè)約束條件，即對(duì)于每個(gè)給定的 a，sin2(a) + cos 2(a)之和等于 1，那么在任何常見(jiàn)角度范圍內(nèi)，sin2(...)和 cos2(...) 的平均值之和必然具有相同的性質(zhì)。我們之前引入了 Sm 來(lái)表示 sin2(...) 的算術(shù)平均數(shù)；采用 Cm 來(lái)表示 cos2(...)，我們可以得到：

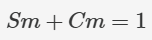
在從 0° 到 360° 的跨度內(nèi)，正弦函數(shù)和余弦函數(shù)都完成了一個(gè)周期；它們產(chǎn)生了兩個(gè)完全相同的波形，只是在時(shí)間上有所偏移。每當(dāng) sin(...) = 0.5 時(shí)，就會(huì)有一個(gè) cos(...) = 0.5 的對(duì)應(yīng)點(diǎn)：

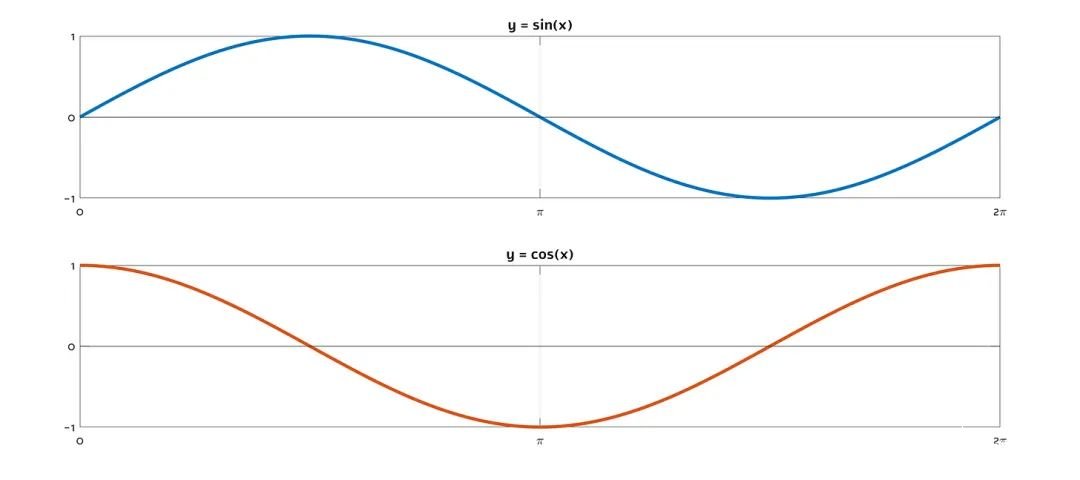
事實(shí)上，我們可以通過(guò)對(duì)余弦部分進(jìn)行一些處理來(lái)說(shuō)明這一點(diǎn)：

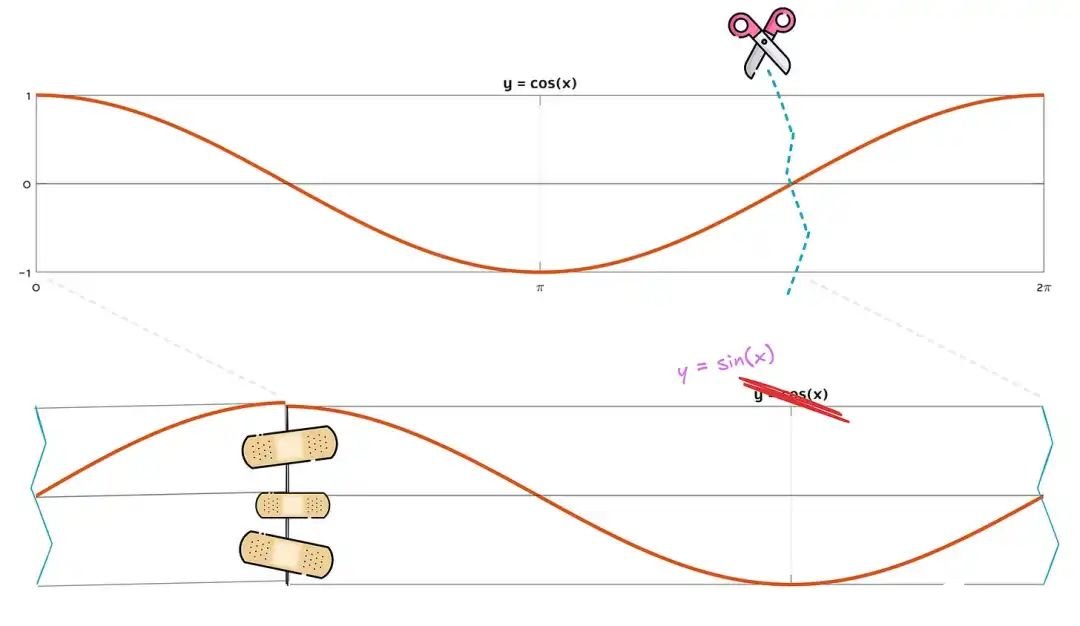
由于波形基本相同，sin(α) 的全周期平均值等于 cos(a) 的全周期平均值。將 sin(a) 和 cos(a) 的每個(gè)值平方并不會(huì)改變這種關(guān)系：我們最終會(huì)得到新的曲線，但它們?nèi)匀皇且粭l直線，而且每條曲線上的任意兩點(diǎn)之間仍然存在 1:1 的對(duì)應(yīng)關(guān)系。sin2(a) 的周期-均值一定與 cos2(a) 的周期-均值相同。根據(jù)這一觀察結(jié)果，我們終于可以算出 Sm 的值：

換句話說(shuō)，我們已經(jīng)確定 sin2(...) 波形在 0° 和 360° 之間的平均值為 ?。將其插入先前的 Vrms 公式，我們就得到了峰值振幅為 Vp 的 0 V 中心正弦波的通用公式：

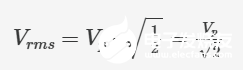
證明完畢，搞定！（小編注：其實(shí)還不如用微積分來(lái)得方便...）

本文轉(zhuǎn)載自（經(jīng)過(guò)編譯及校對(duì)）： https://lcamtuf.substack.com/p/whats-root-mean-square-voltage

注意：如果想第一時(shí)間收到 KiCad 內(nèi)容推送，請(qǐng)點(diǎn)擊下方的名片，按關(guān)注，再設(shè)為星標(biāo)。

常用合集匯總：

和 Dr Peter 一起學(xué) KiCad

KiCad 8 探秘合集

KiCad 使用經(jīng)驗(yàn)分享

KiCad 設(shè)計(jì)項(xiàng)目（Made with KiCad）

常見(jiàn)問(wèn)題與解決方法

KiCad 開(kāi)發(fā)筆記

插件應(yīng)用

發(fā)布記錄

審核編輯 黃宇