正弦波形的RMS或有效值提供與等效直流電源相同的加熱效果

在我們關(guān)于交流波形的教程中，我們簡(jiǎn)要介紹了RMS電壓正弦波形的值，并表示該RMS值與等效直流功率具有相同的加熱效果，在本教程中，我們將通過更詳細(xì)地查看RMS電壓和電流來進(jìn)一步擴(kuò)展該理論。

術(shù)語(yǔ)“RMS”代表“Root-Mean-Squared”。大多數(shù)書籍將此定義為“產(chǎn)生與等效直流電源相同的加熱效果的交流電量”，或者沿著這些線路類似的東西，但RMS值不僅僅是這個(gè)。 RMS值是瞬時(shí)值的平方函數(shù)的平均值（平均值）的平方根。用于定義RMS值的符號(hào)為 V RMS 或 I RMS 。

術(shù)語(yǔ)RMS，僅指時(shí)變正弦電壓，電流或復(fù)雜波形是波形隨時(shí)間變化的幅度，并且不用于直流電路分析或計(jì)算，其幅度始終是恒定的。當(dāng)用于比較交流正弦波形的等效RMS電壓值作為等效直流電路時(shí)，RMS值被稱為“有效值”，通常表示為： V eff 或 I eff 。

換句話說，有效值是等效的DC值，告訴你，在產(chǎn)生相同功率的能力方面，時(shí)變正弦波形等于多少伏特或安培的直流電壓。

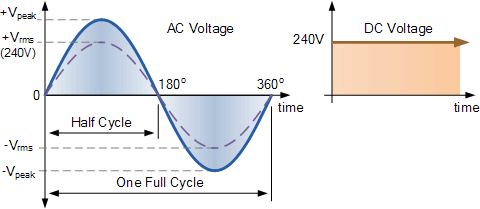
例如，英國(guó)的國(guó)內(nèi)主電源是240Vac 。假設(shè)該值表示“240伏特rms”的有效值。這意味著來自英國(guó)家庭墻壁插座的正弦均方根電壓能夠產(chǎn)生與240伏穩(wěn)定直流電壓相同的平均正電壓，如下所示。

RMS電壓等效值

那么我們?nèi)绾斡?jì)算正弦波形的RMS電壓。正弦波或復(fù)雜波形的RMS電壓可以通過兩種基本方法確定。

圖形方法 - 可以是用于通過在波形上繪制多個(gè)中點(diǎn)來找到任何非正弦時(shí)變波形的RMS值。

分析方法 -is使用微積分找出任何周期性電壓或電流的有效或RMS值的數(shù)學(xué)過程。

RMS電壓圖形方法

雖然計(jì)算方法相同兩個(gè)交流波形的一半，在這個(gè)例子中，我們只考慮正半周期。通過沿波形采用等間隔的瞬時(shí)值，可以以合理的精度找到波形的有效值或均方根值。

波形的正半部分為任意數(shù)量的“n”相等的部分或中間坐標(biāo)以及沿波形繪制的中間坐標(biāo)越多，最終結(jié)果就越準(zhǔn)確。因此，每個(gè)中坐標(biāo)的寬度將是 n o 度，每個(gè)中坐標(biāo)的高度將等于此時(shí)沿波形的波形的瞬時(shí)值。波形的x軸。

圖形方法

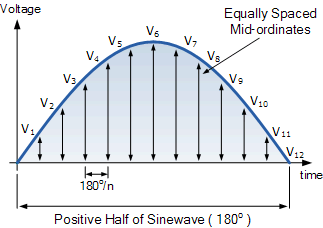
每個(gè)中間值波形（在這種情況下為電壓波形）乘以其自身（平方）并加到下一個(gè)波形。該方法為我們提供了RMS電壓表達(dá)式的“square”或Squared部分。接下來，這個(gè)平方值除以用于給出RMS電壓表達(dá)式的平均值部分的中間坐標(biāo)數(shù)，在上面的簡(jiǎn)單示例中，使用的中間坐標(biāo)數(shù)為12（12） ）。最后，發(fā)現(xiàn)前一個(gè)結(jié)果的平方根給出了RMS電壓的Root部分。

然后我們可以定義用于描述均方根電壓的術(shù)語(yǔ)（V RMS ）為“電壓中點(diǎn)平方 平均的平方根波形“并且這被給出為：

對(duì)于上面的簡(jiǎn)單示例，RMS電壓將計(jì)算為：

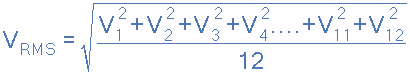
因此我們假設(shè)交流電壓的峰值電壓（ V pk ）為20伏特和取10個(gè)中間坐標(biāo)值發(fā)現(xiàn)變化超過半個(gè)周期如下：

RMS電壓因此計(jì)算如下：

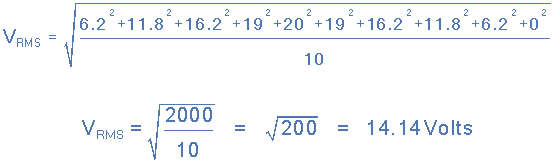
然后使用圖形方法的RMS電壓值如下： 14.14 Volts 。

RMS電壓分析方法

上面的圖形方法是一種非常好的方法找到本質(zhì)上不對(duì)稱或正弦的交替波形的有效或RMS電壓（或電流）。換句話說，波形形狀類似于復(fù)雜波形。然而，當(dāng)處理純正弦波形時(shí)，我們可以通過使用分析或數(shù)學(xué)方法找到RMS值，使我們自己的生活更輕松。

周期性正弦電壓是常數(shù)，可以定義為 V （t） = V max * cos（ωt），周期為 T 。然后我們可以計(jì)算出正弦電壓（V （t））的均方根（rms）值：

通過從0到360 o 或“T”的限制進(jìn)行整合，期間給出：

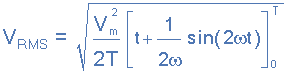
其中： Vm 是波形的峰值或最大值。進(jìn)一步劃分為ω=2π/ T ，上面的復(fù)雜方程最終也會(huì)減少：

RMS電壓方程

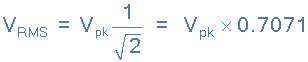
然后RMS電壓（ V RMS ）通過將峰值電壓值乘以0.7071來確定正弦波形，這與將其除以2的平方根（ 1 /√ 2 ）。 RMS電壓（也可稱為有效值）取決于波形的大小，并不是波形頻率或相位角的函數(shù)。

從上面的圖形示例中，波形的峰值電壓（ V pk ）為20伏特。通過使用剛剛定義的分析方法，我們可以將RMS電壓計(jì)算為：

V RMS = V pk * 0.7071 = 20x0。 7071 = 14.14V

請(qǐng)注意， 14.14伏的值與上一個(gè)圖形方法的值相同。然后我們可以使用中坐標(biāo)的圖形方法或計(jì)算的分析方法來找出正弦波形的RMS電壓或電流值。

注意將峰值或最大值乘以常數(shù) 0.7071 ，ONLY適用于正弦波形。對(duì)于非正弦波形，必須使用圖形方法。

但是，除了使用正弦曲線的峰值或最大值，我們還可以使用峰峰值（V PP ）值或平均值（V AVG ）值，以查找正弦曲線等效均方根值，如下所示：

正弦RMS值

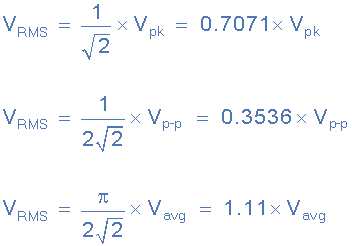
RMS電壓匯總

然后總結(jié)一下。當(dāng)處理交流電壓（或電流）時(shí)，我們面臨著如何表示電壓或信號(hào)幅度的問題。一種簡(jiǎn)單的方法是使用波形的峰值。另一種常用的方法是使用有效值，這也是其更常見的均方根表達(dá)式或簡(jiǎn)稱為RMS值。

均方根，RMS值正弦曲線與所有瞬時(shí)值的平均值不同。電壓的RMS值與電壓的最大值之比與電流的RMS值與電流的最大值之比相同。

大多數(shù)萬(wàn)用表，電壓表或電流表，假設(shè)純正弦波形測(cè)量RMS值。為了找到非正弦波形的RMS值，需要“真有效值萬(wàn)用表”。

正弦波形的RMS值與相同值的直流電流具有相同的加熱效果。也就是說，如果直流電流 I 通過 R ohms 的電阻，則電阻器消耗的直流功率因此將 I 2 R 瓦特。然后，如果交流電流 i max *sinθ流過相同的電阻，則轉(zhuǎn)換為熱量的交流電將為： I 2 rms * R 瓦特。

然后在處理交流電壓和電流時(shí)，除非另有說明，否則應(yīng)將它們視為RMS值。因此，10安培的交流電流將具有與10安培的直流電流相同的加熱效果，最大值為14.14安培。

現(xiàn)已確定交流電壓（或電流）波形的RMS值在下一個(gè)教程中，我們將研究計(jì)算交流電壓的平均值， V AVG ，最后比較兩者。