前一段時間做了一個數(shù)字識別的小系統(tǒng)，基于BP神經(jīng)網(wǎng)絡(luò)算法的，用MFC做的交互。在實現(xiàn)過程中也試著去找一些源碼，總體上來講，這些源碼的可移植性都不好，多數(shù)將交互部分和核心算法代碼雜糅在一起，這樣不僅代碼閱讀困難，而且重要的是核心算法不具備可移植性。設(shè)計模式，設(shè)計模式的重要性啊！于是自己將BP神經(jīng)網(wǎng)絡(luò)的核心算法用標(biāo)準(zhǔn)C++實現(xiàn)，這樣可移植性就有保證的，然后在核心算法上實現(xiàn)基于不同GUI庫的交互（MFC，QT）是能很快的搭建好系統(tǒng)的。下面邊介紹BP算法的原理（請看《數(shù)字圖像處理與機器視覺》非常適合做工程的伙伴），邊給出代碼的實現(xiàn)，最后給出基于核心算法構(gòu)建交互的例子。

人工神經(jīng)網(wǎng)絡(luò)的理論基礎(chǔ)

1.感知器

感知器是一種具有簡單的兩種輸出的人工神經(jīng)元，如下圖所示。

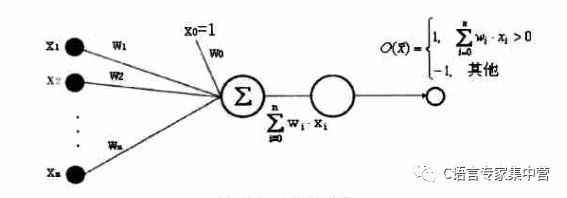
2.線性單元

只有1和-1兩種輸出的感知器實際上限制了其處理和分類的能力，下圖是一種簡單的推廣，即不帶閾值的感知器。

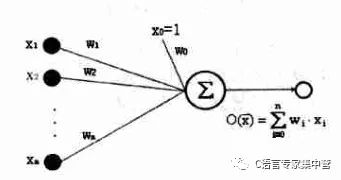
3.誤差準(zhǔn)則

使用的是一個常用的誤差度量標(biāo)準(zhǔn)，平方誤差準(zhǔn)則。公式如下。

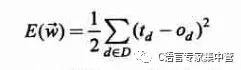
其中D為訓(xùn)練樣本，td為訓(xùn)練觀測值d的訓(xùn)練輸出，ot為觀測值d的實際觀測值。如果是個凸函數(shù)就好了（搞數(shù)學(xué)的，一聽到凸函數(shù)就很高興，呵呵！），但還是可以用梯度下降的方法求其參數(shù)w。

4.梯度下降推導(dǎo)

在高等數(shù)學(xué)中梯度的概念實際上就是一個方向向量，也就是方向?qū)?shù)最大的方向，也就是說沿著這個方向，函數(shù)值的變化速度最快。我們這里是做梯度下降，那么就是沿著梯度的負(fù)方向更新參數(shù)w的值來快速達(dá)到E函數(shù)值的最小了。這樣梯度下降算法的步驟基本如下：

1）初始化參數(shù)w（隨機，或其它方法）。

2）求梯度。

3）沿梯度方向更新參數(shù)w，可以添加一個學(xué)習(xí)率，也就是按多大的步子下降。

4）重復(fù)1），2），3）直到達(dá)到設(shè)置的條件（迭代次數(shù)，或者E的減小量小于某個閾值）。

梯度的表達(dá)式如下：

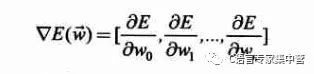
那么如何求梯度呢？就是復(fù)合函數(shù)求導(dǎo)的過程，如下：

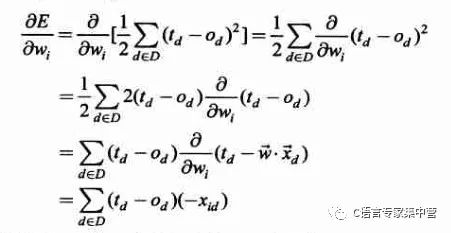
其中xid為樣本中第d個觀測值對應(yīng)的一個輸入分量xi。這樣，訓(xùn)練過程中參數(shù)w的更新表達(dá)式如下（其中添加了一個學(xué)習(xí)率，也就是下降的步長）：

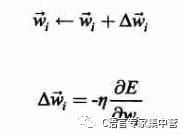
于是參數(shù)wi的更新增量為：

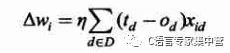
對于學(xué)習(xí)率選擇的問題，一般較小是能夠保證收斂的，看下圖吧。

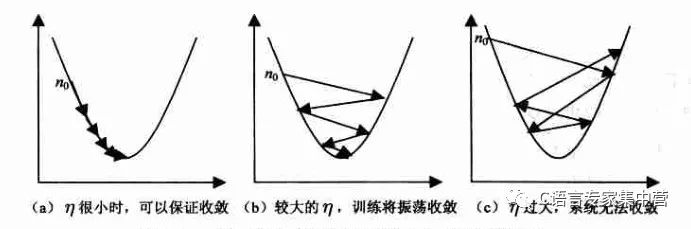
5.增量梯度下降

對于4中的梯度下降算法，其缺點是有時收斂速度慢，如果在誤差曲面上存在多個局部極小值，算法不能保證能夠找到全局極小值。為了改善這些缺點，提出了增量梯度下降算法。增量梯度下降，與4中的梯度下降的不同之處在于，4中對參數(shù)w的更新是根據(jù)整個樣本中的觀測值的誤差來計算的，而增量梯度下降算法是根據(jù)樣本中單個觀測值的誤差來計算w的更新。

6.梯度檢驗

這是一個比較實用的內(nèi)容，如何確定自己的代碼就一定沒有錯呢？因為在求梯度的時候是很容易犯錯誤的，我就犯過了，嗨，調(diào)了兩天才找出來，一個數(shù)組下表寫錯了，要是早一點看看斯坦福大學(xué)的深度學(xué)習(xí)基礎(chǔ)教程就好了，這里只是截圖一部分，有時間去仔細(xì)看看吧。

多層神經(jīng)網(wǎng)絡(luò)

好了有了前面的基礎(chǔ)，我們現(xiàn)在就可以進(jìn)行實戰(zhàn)了，構(gòu)造多層神經(jīng)網(wǎng)絡(luò)。

1.Sigmoid神經(jīng)元

Sigmoid神經(jīng)元可由下圖表示：

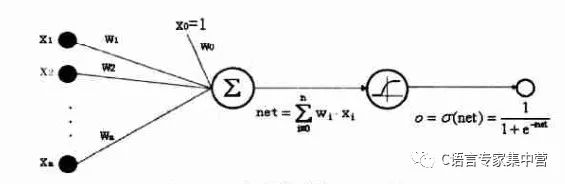
2.神經(jīng)網(wǎng)絡(luò)層

一個三層的BP神經(jīng)網(wǎng)絡(luò)可由下圖表示：

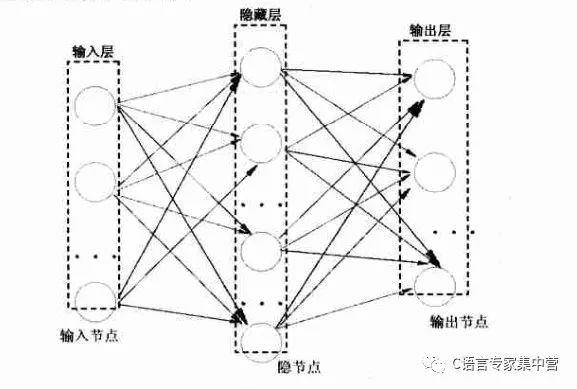
3.神經(jīng)元和神經(jīng)網(wǎng)絡(luò)層的標(biāo)準(zhǔn)C++定義

由2中的三層BP神經(jīng)網(wǎng)絡(luò)的示意圖中可以看出，隱藏層和輸出層是具有類似的結(jié)構(gòu)的。神經(jīng)元和神經(jīng)網(wǎng)絡(luò)層的定義如下：