相關函數:外衣不神秘,先剝開看看
信號啊信號,多想將你蹂躪,事實上,卻反被蹂躪至死 …
信號到底是個什么東西,千百年來為何無數先人前赴后繼,說白了就是電磁波;深了點就是電磁波的形狀包含了信息;再深了點就是電磁波的形狀被編了碼或加了密;歸根究底,就是電磁波嘛,只不過像是雕刻藝術一樣搞得富含”深意”,或圓潤,或線條錯亂,或姿態妖嬈…【shape請自行腦補】
【對不起,好像扯遠了,那么重點來了,快劃!】
相關函數是干嘛滴!誰搞出來滴!搞出來干嘛滴!這都是需要好好想一想滴!
舉個例子先:為什么序列的自相關函數可以體現出隨機性?一串由+1,-1組成的序列完全隨機,另外一個序列也完全隨機一一OK, 相乘的結果肯定有一半是-1,一半是+1,全部加起來肯定是0。一個完全隨機的序列,他進行N拍延遲后得到的一定是另外一個完全隨機的序列。如果你同意上一段話,那么后面不需要我解釋了吧。如果序列的隨機性不夠,則一一相乘得到的+1和-1個數不相等,全部加起來的結果就不是0,隨機性越差,結果之絕對值就越大。
所以我們看到了什么:信號的相關函數透露了一個秘密,現在的我和N年之后的我有多相似。
互相關函數
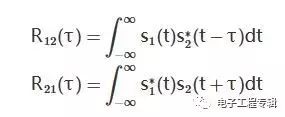
自相關函數
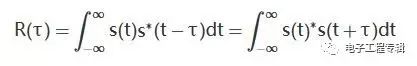
通俗的講,所謂相關函數的性質,差不多就是一個人有哪些特點的意思了
共軛對稱R(τ)=R?(?τ);
自相關原點值equal to信號能量R(τ=0)=∫∞?∞s(t)s?(t?0)dt;
相關函數的面積equal to信號面積模的平方;【這個畫圖才行】
F[R(τ)]為實數
若兩信號頻域上能量譜相同,時域波形不同,則兩信號相關函數相同
信號卷積:與相關函數傻傻混淆
前面相關函數已作說明,那么卷積又是什么呢,有那么麻煩嗎? 不推薦用“反轉/翻轉/反褶/對稱”等解釋卷積。好好的信號為什么要翻轉?導致學生難以理解卷積的物理意義。
這個其實非常簡單的概念,國內的大多數教材卻沒有講透。
直接看圖,不信看不懂。以離散信號為例,連續信號同理。
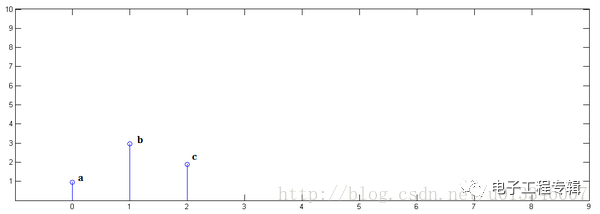
已知x[0]=a,x[1]=b,x[2]=c:
已知y[0]=i,y[1]=j,y[2]=k:
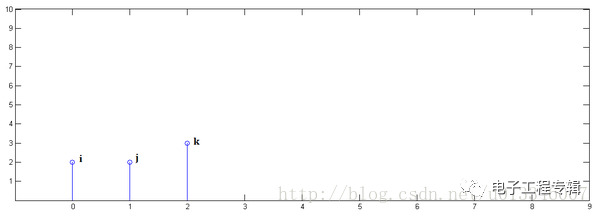
下面通過演示求x[n] * y[n]的過程,揭示卷積的物理意義。
第一步,x[n]乘以y[0]并平移到位置0:
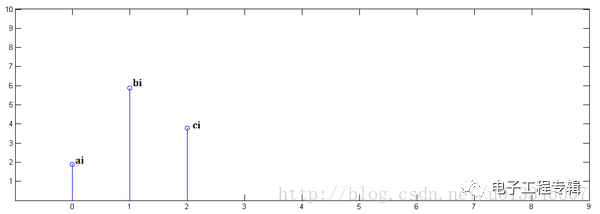
第二步,x[n]乘以y[1]并平移到位置1:
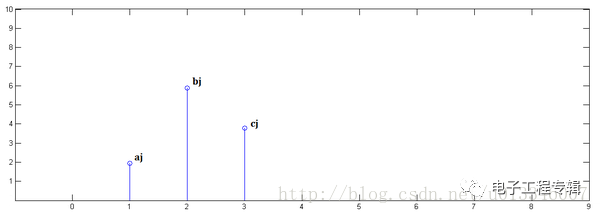
第三步,x[n]乘以y[2]并平移到位置2:
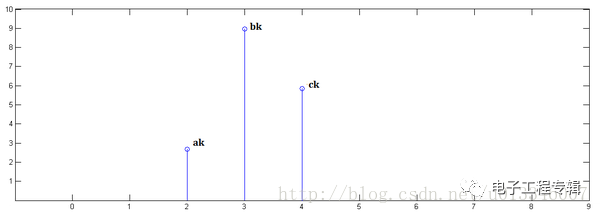
最后,把上面三個圖疊加,就得到了x[n] * y[n]:
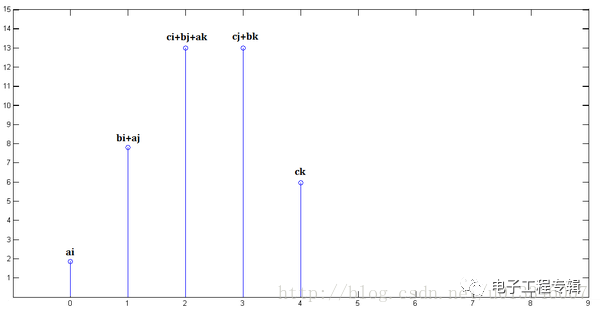
所以呢,卷積就是加權求和,通俗的說: 在輸入信號的每個位置,疊加一個單位響應,就得到了輸出信號。 這正是單位響應是如此重要的原因。
下面搬搬搬,知乎大神實在太厲害,不得不佩服:復利的例子來理解卷積可能更好理解一些:
小明存入100元錢,年利率是5%,按復利計算(即將每一年所獲利息加入本金,以計算下一年的利息),那么在五年之后他能拿到的錢數是,如下表所示: 
將這筆錢存入銀行的一年之后,小明又往銀行中存入了100元錢,年利率仍為5%,那么這筆錢按復利計算,到了第五年,將收回的錢數是100(1+5\%)^4,我們將這一結果作為新的一行加入上面的表格中:

以此類推,如果小明每年都往銀行中存入新的100元錢,那么這個收益表格將是這樣的:
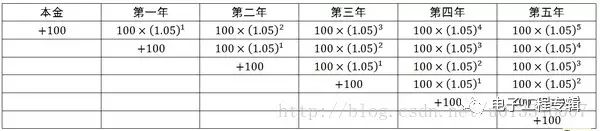
可見,最終小明拿到的錢將等于他各年存入的錢分別計算復利之后得到的錢數的總和,即:

用求和符號來簡化這個公式,可以得到: 
在上式中,為小明的存錢函數,而為存入銀行的每一筆錢的復利計算函數。在這里,小明最終得到的錢就是他的存錢函數和復利計算函數的卷積。
為了更清晰地看到這一點,我們將這個公式推廣到連續的情況,也就是說,小明在從到的這一段時間內,每時每刻都往銀行里存錢,他的存錢函數為,而銀行也對他存入的每一筆錢按復利公式計算收益,則小明到時間將得到的總錢數為:
這也就是卷積的表達式了,上式可以記為。 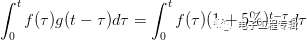 相信通過上面這個例子,大家應該能夠很清晰地記住卷積公式了。
相信通過上面這個例子,大家應該能夠很清晰地記住卷積公式了。
下面我們再展開說兩句: 如果我們將小明的存款函數視為一個信號發生(也就是輸入/激勵)的過程,而將復利函數視為一個系統對信號的響應函數(也就是反饋/響應),那么二者的卷積就可以看做是在時刻對系統進行觀察,得到的觀察結果(也就是輸出)將是過去產生的所有信號經過系統的「處理/響應」后得到的結果的疊加,這也就是卷積的物理意義了。
此處請注意卷積公式,對比相關函數公式,你會發現有意思的事情
輸入信號:s1(t) ,沖激響應:s2(t)
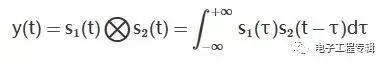
此處放上相關函數公式,方便對比:
互相關函數
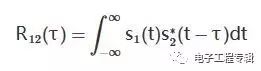
是不是可以發現點interesting的地方,get 一下點:
神奇的公式:R12(τ)=s1(τ)?s?2(?τ)
卷積的性質,脾氣怎么y
可交換/可結合/可分配,記住這個就行
相關與卷積的區別
相關公式和卷積公式很像,相關能利用卷積表示,所以有人覺得兩個概念有關系,其實二者從概念上沒有聯系。
相關運算中被積函數沒有時間反褶的過程,而卷積運算中有。
相關函數不滿足交換,而卷積可以。
Matlab中的函數
Cross-correlation(互相關)
兩個離散時間序列的互相關【圖片沒太搞明白。。。】

Convolution(卷積)
兩個向量u,v的卷積輸出【圖片還是沒太搞明白。。。再( ╯□╰ )】

仿真分析
仿真結果
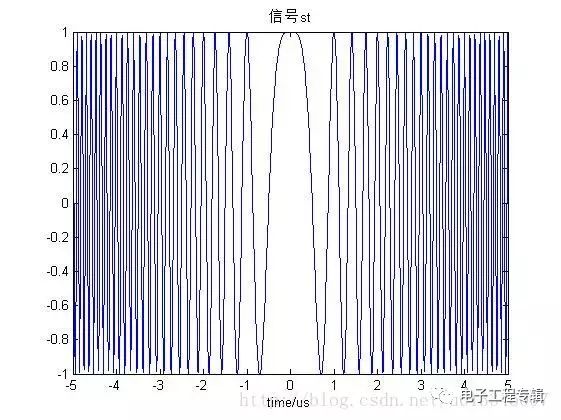
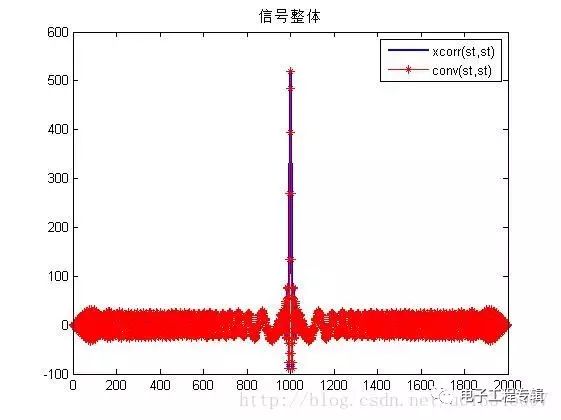
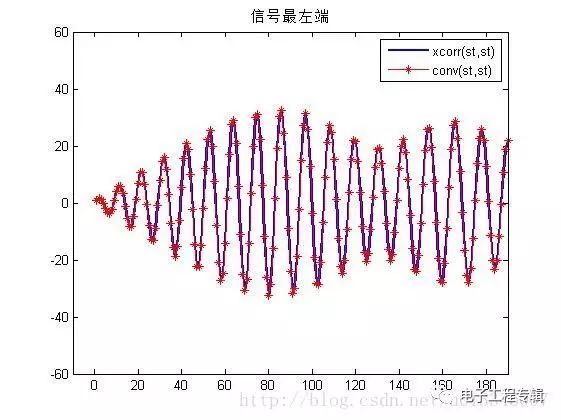
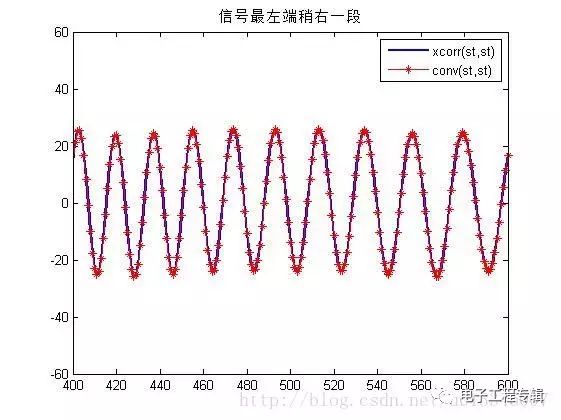
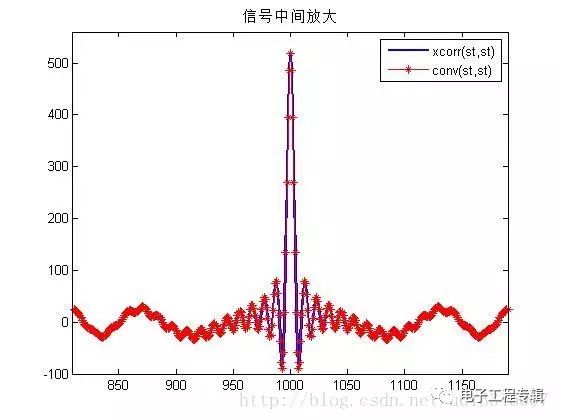
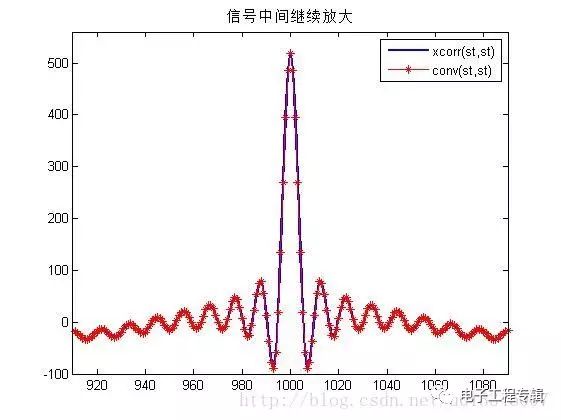
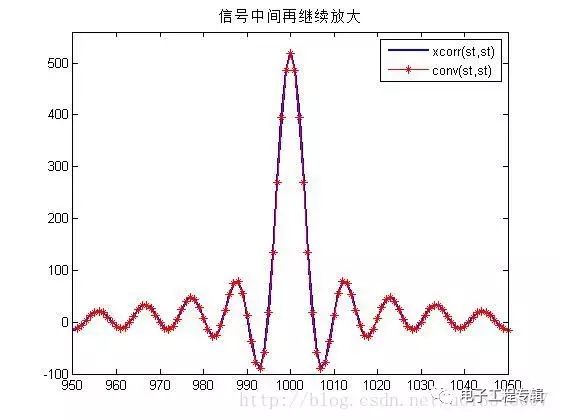
在上面的仿真中,自相關函數等于其與自身的卷積!!發現沒有!!!符合get的點!!!!哈哈哈 R12(τ)=s1(τ)?s?2(?τ)
-
信號
+關注
關注
11文章
2847瀏覽量
78029 -
電磁波
+關注
關注
21文章
1479瀏覽量
54527 -
函數
+關注
關注
3文章
4375瀏覽量
64480
原文標題:信號處理繞不過去的坎:相關與卷積
文章出處:【微信號:eet-china,微信公眾號:電子工程專輯】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
使用TLV320AIC3254EVM-K評估AIC3254,如何測試才能體現出ENC模塊的作用?
STM32F10xx 芯片由絲印所體現出的共同點和區別
什么是自相關?如何將它應用到Python中的一個簡單數據集
ESP32-S2 TRM(V1.0) 217頁中的中斷源表并沒有在 IDF 相關文件中體現出來?只有ESP32的中斷源表?
二元推導隨機性檢測的優化實現
基于FPGA嵌入式的多比特自相關器設計

面向HC256,RC4利用NOST進行系統隨機性檢測
“隨機性電源即插即用關鍵技術研究及應用”通過驗收
為什么區塊鏈可信隨機性如此重要
以太坊區塊鏈是如何產生隨機性的
AI的“隨機性”挑戰:它們比人類更“不隨機”?






 為什么序列的自相關函數可以體現出隨機性?
為什么序列的自相關函數可以體現出隨機性?












評論