來(lái)源:OpenFPGA;作者:碎碎思
在創(chuàng)建 RTL 示例時(shí),經(jīng)常使用 VHDL 2008 附帶的 VHDL 包。它提供了出色的功能,可以高效地處理定點(diǎn)數(shù),當(dāng)然,它們也是可綜合的。該包的一些優(yōu)點(diǎn)包括:
有符號(hào)和無(wú)符號(hào)(后綴和后綴)定點(diǎn)向量。
輕松將定點(diǎn)數(shù)表示并量化為定點(diǎn)向量。
小數(shù)點(diǎn)位于向量元素 0 和 -1 之間。這樣就無(wú)需在運(yùn)算過(guò)程中跟蹤小數(shù)點(diǎn)以進(jìn)行對(duì)齊(大量運(yùn)算這點(diǎn)很難把握)。
運(yùn)算的溢出、舍入和范圍管理有明確的定義。
算術(shù)和比較運(yùn)算符。
因此,當(dāng)需要實(shí)現(xiàn)算法時(shí),我會(huì)使用這個(gè)包。但是實(shí)際應(yīng)用時(shí),還會(huì)有很多浮點(diǎn)運(yùn)算。
自然而然地,一個(gè)問(wèn)題出現(xiàn)了:用定點(diǎn)和浮點(diǎn)實(shí)現(xiàn)同一個(gè)方程時(shí),資源有什么區(qū)別?
我們將要看的例子是如何利用多項(xiàng)式近似地將ADC讀數(shù)轉(zhuǎn)換為溫度值。這在工業(yè)應(yīng)用中很常見(jiàn)(使用鉑電阻溫度計(jì)時(shí))。
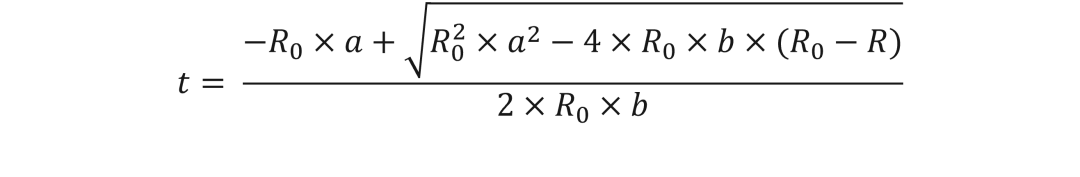
要實(shí)現(xiàn)的具體方程是 y = 2E-09x4 - 4E-07x3 + 0.011x2 + 2.403x - 251.26,該方程是從繪制方程式中提取出來(lái)的。雖然我們可以直接實(shí)現(xiàn)該方程,但這會(huì)非常浪費(fèi)資源,還會(huì)增加開(kāi)發(fā)的復(fù)雜性和風(fēng)險(xiǎn)。
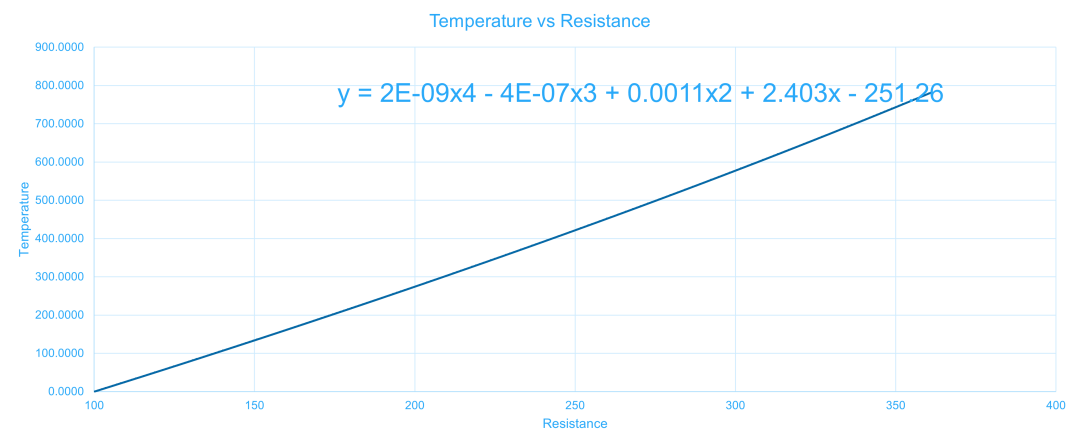
使用定點(diǎn)數(shù)系統(tǒng),我們需要做一些量化來(lái)保持精度和準(zhǔn)確度。
代碼和一個(gè)簡(jiǎn)單的仿真如下。
library IEEE; use IEEE.STD_LOGIC_1164.ALL; use ieee.fixed_pkg.all; entity complex_example is port( clk :instd_logic; ip :instd_logic_vector(7 downto 0); op : out std_logic_vector(8 downto 0)); end complex_example; architecture Behavioral of complex_example is signal power_a : sfixed(8 downto -32):=(others=>'0'); signal power_b : sfixed(8 downto -32):=(others=>'0'); signal power_c : sfixed(8 downto -32):=(others=>'0'); signal calc : sfixed(8 downto -32) :=(others=>'0'); signal store : sfixed(8 downto 0) := (others =>'0'); constant a : sfixed(8 downto -32):= to_sfixed( 2.00E-09, 8,-32 ); constant b : sfixed(8 downto -32):= to_sfixed( 4.00E-07, 8,-32 ); constant c : sfixed(8 downto -32):= to_sfixed( 0.0011, 8,-32 ); constant d : sfixed(8 downto -32):= to_sfixed( 2.403, 8,-32 ); constant e : sfixed(8 downto -32):= to_sfixed( 251.26, 8,-32 ); typereg_array is array (9 downto 0) of sfixed(8 downto -32); signal pipeline_reg : reg_array; begin cvd : process(clk) begin ifrising_edge(clk)then store <= to_sfixed('0'&ip,store); ? ? power_a <= resize (arg => power_b * store * a, size_res => power_a); power_b <= resize (arg => power_c * store * b, size_res => power_b); power_c <= resize (arg => store * store * c, size_res => power_c); calc <= resize (arg => power_a - power_b + power_c + (store * d) - e, size_res => calc); pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) & calc; ? ? ?? ?op <= to_slv(pipeline_reg(pipeline_reg'high)(8 downto 0)); ? end?if; end process; end Behavioral;
對(duì)于 109 Ω的電阻輸入,溫度應(yīng)報(bào)告為 23.7°C。我們可以在下面的定點(diǎn)仿真中看到,結(jié)果符合預(yù)期,精度在可接受的范圍內(nèi)。
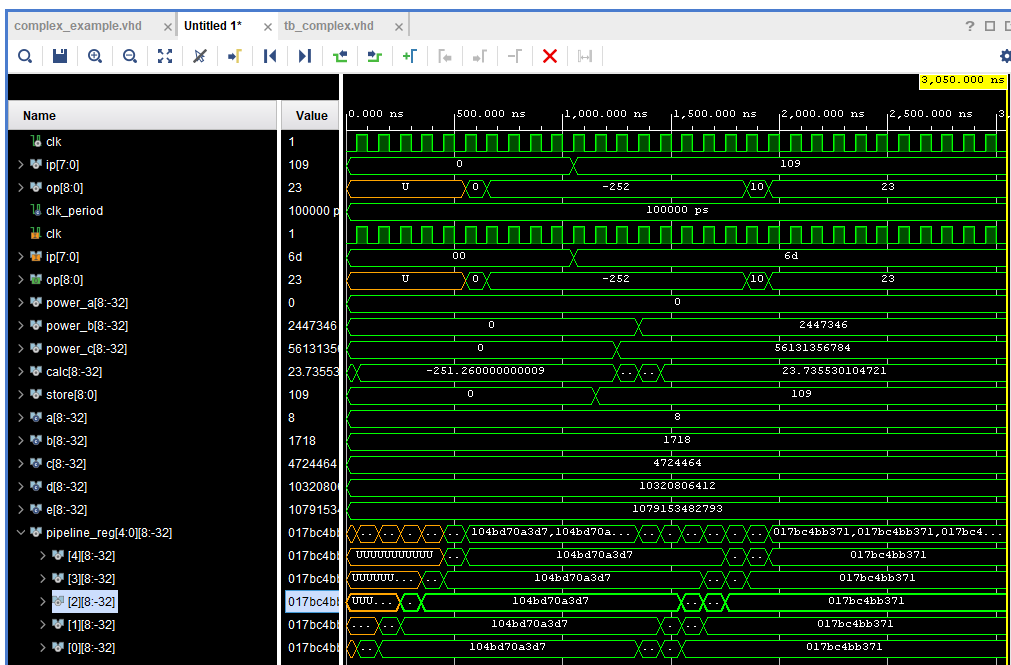
使用浮點(diǎn)包實(shí)現(xiàn)相同的功能,以類似的方式實(shí)現(xiàn)
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.FLOAT_pkg.ALL; -- Use the floating-point package
entity FloatingPointPolynomial is
Port (
clk :inSTD_LOGIC;
x :infloat32; -- Input x as a 32-bit floating-point number
y : out float32 -- Output y as a 32-bit floating-point number );
end FloatingPointPolynomial;
architecture Behavioral of FloatingPointPolynomial is
-- Define constantsforthe polynomial coefficients
constant a4 : float32 := TO_float(2.00E-09);
constant a3 : float32 := TO_float(-4.00E-07);
constant a2 : float32 := TO_float(0.011);
constant a1 : float32 := TO_float(2.403);
constant a0 : float32 := TO_float(-251.26);
signal x2, x3, x4 : float32; -- Intermediate powers of x
signal term4, term3, term2, term1 : float32; -- Polynomial terms
signal res : float32;
typereg_array is array (9 downto 0) of float32;
signal pipeline_reg : reg_array;
begin
process(clk)
begin
ifrising_edge(clk)then
-- Calculate powers of x
x2 <= x * x;
? ? ? ? ? ? x3 <= x2 * x;
? ? ? ? ? ? x4 <= x3 * x;
? ? ? ? ? ? -- Calculate each term?in?the polynomial
? ? ? ? ? ? term4 <= a4 * x4;
? ? ? ? ? ? term3 <= a3 * x3;
? ? ? ? ? ? term2 <= a2 * x2;
? ? ? ? ? ? term1 <= a1 * x;
? ? ? ? ? ? -- Calculate final result
? ? ? ? ? ? res <= term4 + term3 + term2 + term1 + a0;
? ? ? ? ? ? pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) &?
? ? ? ?res;
? ? ? ? ? ? y <= (pipeline_reg(pipeline_reg'high));
? ? ? ? end?if;
? ? end process;
end Behavioral;
仿真再次顯示了預(yù)期的結(jié)果,作為浮點(diǎn)結(jié)果,我們得到的結(jié)果也包括分?jǐn)?shù)元素。
因此,定點(diǎn)和浮點(diǎn)都能夠?qū)崿F(xiàn)定義的算法。
為了了解利用所需的資源,決定將這兩種算數(shù)實(shí)現(xiàn)都以 K26 SoM 為目標(biāo)進(jìn)行綜合。
運(yùn)行綜合將識(shí)別每個(gè)模塊所需的資源。
正如預(yù)期的那樣,定點(diǎn)實(shí)現(xiàn)所需的邏輯占用空間比浮點(diǎn)實(shí)現(xiàn)所需的小得多。
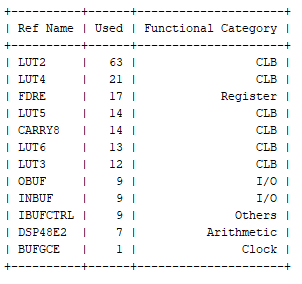
定點(diǎn)實(shí)現(xiàn)
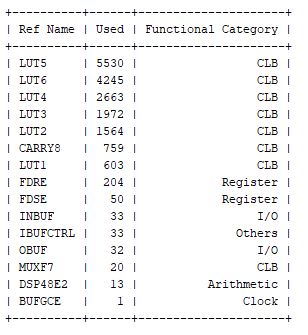
浮點(diǎn)實(shí)現(xiàn)
我們不僅需要考慮邏輯占用空間,還需要考慮時(shí)序性能。考慮到這一點(diǎn),將兩個(gè)設(shè)計(jì)都設(shè)置為 200 MHz 運(yùn)行,并從一開(kāi)始就實(shí)現(xiàn)了基準(zhǔn)時(shí)序收斂。
實(shí)現(xiàn)時(shí)序收斂比定點(diǎn)收斂更重要,這在浮點(diǎn)實(shí)現(xiàn)中是可以預(yù)料到的。不得不重新審視設(shè)計(jì),并在幾個(gè)關(guān)鍵階段實(shí)現(xiàn)流水線,因?yàn)樽畛醯拇a只是為了確定占用空間的差異。
值得注意的是,Versal 系列中的 DSP58 支持浮點(diǎn)運(yùn)算,但它不能直接從 float32 映射到 DSP。為了利用此功能,我們需要實(shí)例化配置為 FP32 操作的 DSP58,或者利用 Vivado IP 集成器提供的浮點(diǎn) IP。
總結(jié)這篇博客,正如預(yù)期的那樣,在使用 VHDL 中的浮點(diǎn)庫(kù)時(shí),邏輯占用空間存在很大差異。
建議在必要時(shí)利用定點(diǎn),并在絕對(duì)必要時(shí)限制浮點(diǎn)。
-
仿真
+關(guān)注
關(guān)注
51文章
4251瀏覽量
135463 -
RTL
+關(guān)注
關(guān)注
1文章
389瀏覽量
60818 -
運(yùn)算符
+關(guān)注
關(guān)注
0文章
173瀏覽量
11393
原文標(biāo)題:FPGA定點(diǎn)和浮點(diǎn)數(shù)學(xué)運(yùn)算-實(shí)例對(duì)比
文章出處:【微信號(hào):FPGA研究院,微信公眾號(hào):FPGA研究院】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
浮點(diǎn)數(shù)與定點(diǎn)數(shù)
【安富萊——DSP教程】第7章 DSP定點(diǎn)數(shù)和浮點(diǎn)數(shù)(重要)
第7章 DSP定點(diǎn)數(shù)和浮點(diǎn)數(shù)
CPU執(zhí)行一個(gè)需要浮點(diǎn)數(shù)運(yùn)算的程序時(shí)有三種方式
定點(diǎn)數(shù)和浮點(diǎn)數(shù)的區(qū)別是什么
如何在GCC中為具有FPU的Cortex M4啟用硬件浮點(diǎn)數(shù)學(xué)運(yùn)算呢?
擴(kuò)充浮點(diǎn)運(yùn)算集是否需要自己在FPGA板子上設(shè)置一個(gè)定點(diǎn)數(shù)轉(zhuǎn)為浮點(diǎn)數(shù)的部分?
在FPGA里浮點(diǎn)數(shù)與定點(diǎn)數(shù)表示法原理展示

單片機(jī)浮點(diǎn)數(shù)運(yùn)算的源碼設(shè)計(jì)

FPGA中浮點(diǎn)運(yùn)算定標(biāo)實(shí)現(xiàn)方法
定點(diǎn)數(shù)和浮點(diǎn)數(shù)在STM32單片機(jī)中使用傅里葉(FFT)變換的理解

如何在FPGA中正確處理浮點(diǎn)數(shù)運(yùn)算
FPGA浮點(diǎn)數(shù)轉(zhuǎn)化為定點(diǎn)數(shù)方法
FPGA浮點(diǎn)數(shù)表示及計(jì)算機(jī)數(shù)值表示規(guī)則
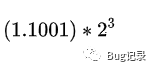
定點(diǎn)數(shù)和浮點(diǎn)數(shù)的概念 浮點(diǎn)數(shù)二進(jìn)制序列與指數(shù)表達(dá)式之間的轉(zhuǎn)化
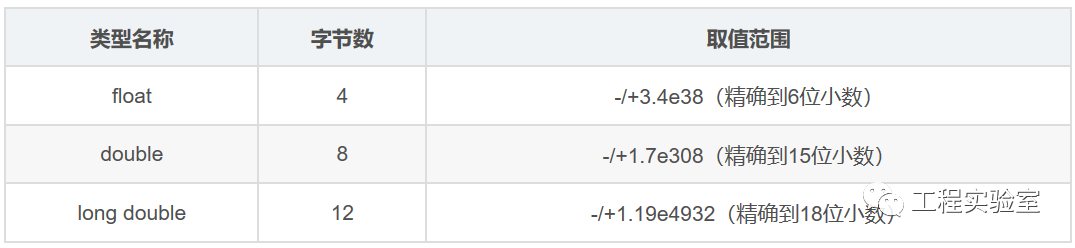





 FPGA定點(diǎn)和浮點(diǎn)數(shù)學(xué)運(yùn)算實(shí)例對(duì)比
FPGA定點(diǎn)和浮點(diǎn)數(shù)學(xué)運(yùn)算實(shí)例對(duì)比










評(píng)論