相對熵，又稱為KL散度（Kullback-Leibler divergence），是兩個概率分布P和Q差別的非對稱性的度量。近日，CMU的助理教授Simon DeDeo就在推特上表示：“用到KL散度的領域十分廣泛，包括心理學、認知學（epistemic）、熱力學、統計學、計算、幾何學等等。關于這個話題我能開一場研討會。”

于是，Simon Dedeo就在他的推特上列出了KL散度在各領域不同的使用情況，并附上相關文章。論智整理編譯如下：

心理學

在心理學領域，KL散度可以作為預測注意力指向哪里的優秀預測器。在美國南加州大學2005年發表的一篇論文中，研究人員用數據流和新穎的數學方法探究了人們在驚訝情況下大腦的反應。他們認為，驚訝是一種一般的、理論上的概念，它可以由第一原理生成，并還可以通過時空尺寸、感覺形態和數據類型及數據來源形成。

利用貝葉斯框架理論，研究人員捕捉到實驗對象的先驗概率分布，然后將背景信息表示為：

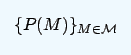
其中模型或假設為M。有了先驗分布，新數據帶來的基本影響D將先驗分布轉換為后驗分布{P(M|D)}，表示為：

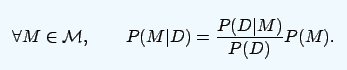
在這個框架中，如果實驗對象的情緒未受影響，那么D就不含有驚訝情緒，即后驗和先驗是一樣的。反之，如果研究對象產生驚訝的情緒，那么后驗和先驗就會產生距離。于是研究人員通過測量后驗和先驗之間的距離，間接地測出是否有驚訝知情。這就用到了KL散度，表示為：

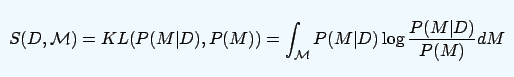
論文地址：ilab.usc.edu/surprise/

認知學

KL散度可以作為決定實驗方向的測量標準（讓模型產生的效果最大化）。通常，T-optimality是用來獲得最優設計，以分辨具有正態分布的同方差模型。該功能經過拓展，還用于研究文學中異方差情況和二元響應模型。在2007年的一篇論文中，來自西班牙和意大利的研究人員提出了一種基于KL距離的新標準，用于區分相應的不具有動態分布的模型。

統計學

KL散度在統計學中的應用可就太多了，但是作者重點討論了它作為測量近似求解法失敗的工具。 在作者曾經寫的博客中有這樣一個例子：假設我們是太空科學家，到了一座遙遠的陌生星球，我們想研究星球上一種蟲子，這種蟲子有10顆牙齒，但是長期生活過后，蟲子的牙齒會脫落一部分，收集了一部分樣本后，我們得到了以下牙齒數量分布：

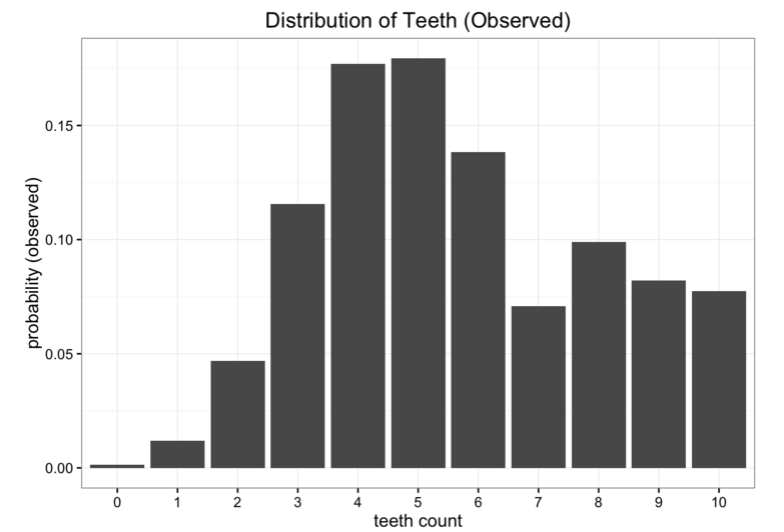
雖然數據很好，但是有一點問題。我們離地球太遠了，傳輸數據回去的成本太高。我們現在想將數據簡化成簡單模型，只保留一兩個參數。其中一種方法是用一種均勻分布的方式表示蟲子的牙齒數量。我們知道一共存在11種可能的情況：

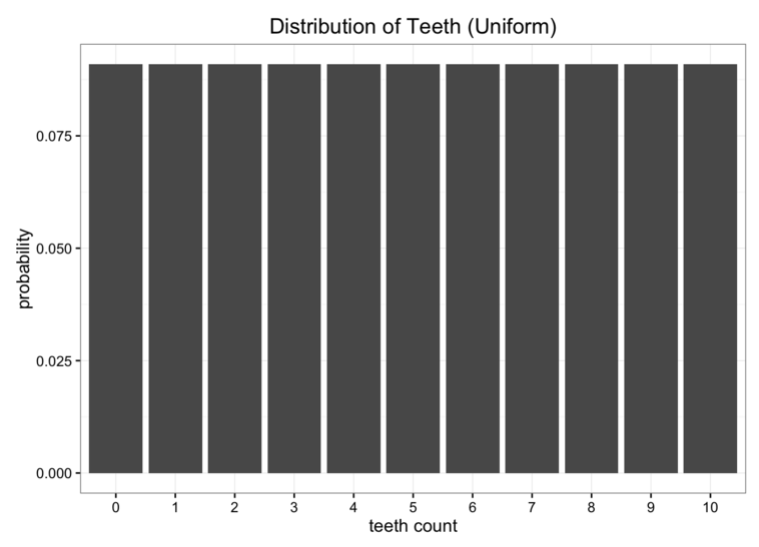
很顯然，我們的數據并不是均勻分布的，但是它看起來也不像我們通常所見的某種分布形態。另一種方法是我們可以試著用二項分布對數據建模。在這個案例中，我們需要做的就是估計二項分布中概率參數。我們知道，假設試驗次數為n，概率為p，那么期望值就是E[x]=n?p。在這個案例中，n=10，期望值就是我們數據的平均數，假設是5.7吧。所以我們對p的最佳估計就是0.57.得到的二項分布如下：

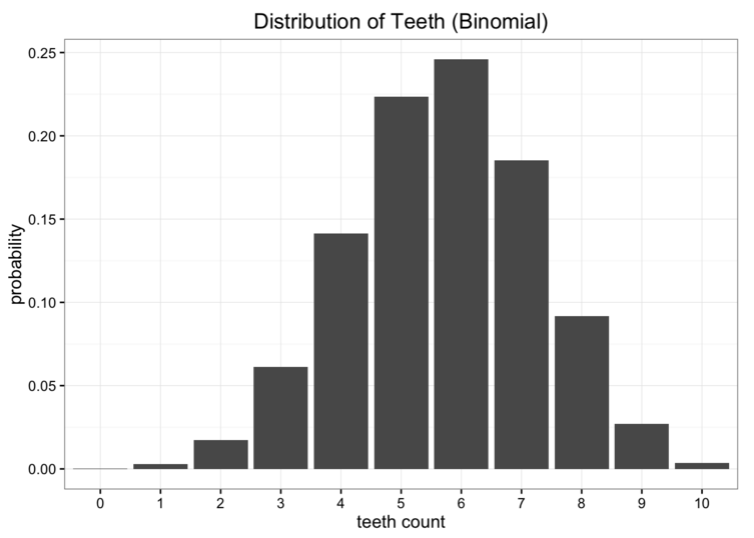
將這些模型與原始數據對比，沒有一個能完美契合的，但是哪個更好呢？

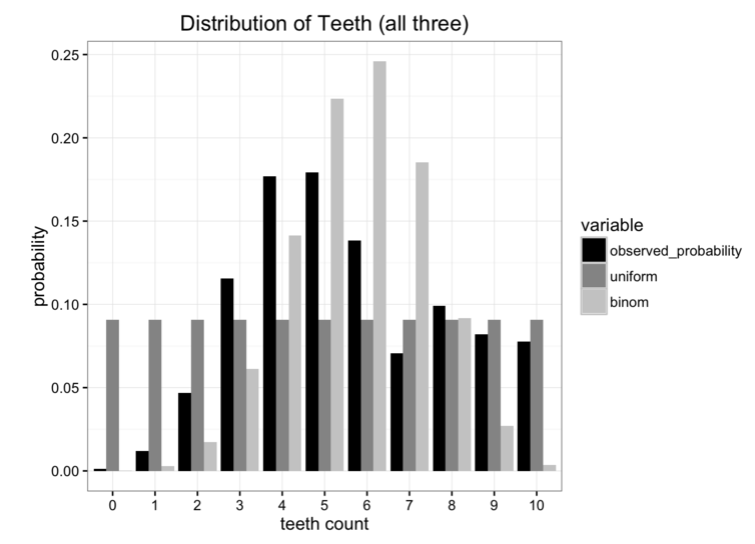
其中雖然存在一些錯誤的指標，但我們最初的目的是盡量減少發送的信息。所以，想要知道那種模型保留了原始數據最多的信息，最好的方法就是用KL散度。

計算（機器學習）

KL散度可以作為檢測模型是否有效的工具，即可以顯示模型留有多少的無用信息。在Still等人2012年發表的一篇論文中，他們為了測試模型的質量，利用KL散度。

另一個機器學習的應用：將KL散度（通常在這種情況下被稱為“交叉熵”）當做自動編碼器、深度學習等的基本損失函數。

另外，還可用作算法公平性（algorithmic fairness）。如何以最佳方式限制一個預測算法，同時還要保證公平。本文作者與2016年發表論文，研究了大數據中的變量問題。

作者認為，當我們用機器學習處理公共政策時，我們發現很多有用的變量與其他一些有問題的變量結合在了一起。這一現象在大數據時代更加嚴重，有些預測根本沒有強有力的理論支撐。如果高質量算法無法提供有力的證明，那么隨意做出決策是非常危險的。為了保證預測的準確性，作者用KL散度對兩種決策進行比較。

論文地址：arxiv.org/abs/1412.4643

計算（壓縮）

當為一種系統設計的壓縮算法無法應用到另一種系統上時，就需要用KL散度進行計算。

文化發展

我們認為KL散度還可以作為研究個人發展與創新人物的測量標準。在2016年的一篇論文中，研究人員認為，在一個不確定資源分布的陌生環境中進行研究，總會在新舊發現中搖擺不定，二者要進行權衡。在查找信息的過程中也是如此，求知若渴的人總會猶豫，是在已知領域深究，還是開發新領域的研究呢？為了研究這一決策過程，他們以達爾文為例，找出了他的閱讀筆記中出現的所有書，并用KL散度生成了一個模型，量化了他的讀書選擇。

論文地址：www.sciencedirect.com/science/article/pii/S0010027716302840

同時，KL散度還能用來研究競爭與合作的創造以及想法的分享。在前不久發表的論文中，美國研究人員就利用KL散度研究在法國大革命期間，人們是如何做出民主決策的。

論文地址：www.pnas.org/content/115/18/4607.short

量子理論

劍橋大學的學生Felix Leditzky寫了一本關于相對熵的介紹及其在量子理論中的應用的博士論文，其中包括KL散度是如何在互換算子的情況下生成量子的。論文共200頁，感興趣的同學可以拜讀一下。

論文地址：pdfs.semanticscholar.org/30a7/6a44a4f0f882c58bd0b636d6393956258c3f.pdf

用戶@postquantum補充：“如果你有一些受限的操作類別，那么KL散度會告訴你你需要多少原材料（研究成果、量子糾纏、信息），這種測量是獨一無二的。”具體可參考論文：arxiv.org/abs/quant-ph/0207177

另外如果你想使用廣義熵和超統計學（即耦合系統），這是Rényi熵的特殊情況。

論文地址：www.pnas.org/content/108/16/6390

數字人文學科

KL散度與TFIDF相關，但是當它涉及粗粒化時，KL散度的性能更好。（特征最明顯的單詞在梳理文件時部分KL較高；停止詞的KL值最低）。具體可查看相關論文。

論文地址：www.mdpi.com/1099-4300/15/6/2246

經濟學

另外，KL散度在經濟學中也有出現，推特用戶@itsaguytalking就發表論文，用KL散度研究不同國家之間的貿易情況，論文研究的目的是如何測量不同意見之間的距離。

論文地址：www.columbia.edu/~ez2197/HowToMeasureDisagreement.pdf

生物學

在2015年的一篇論文中，研究者Nihat Ay認為，隨機交互單元的相互依賴型通常由靜態聯合概率分布的KL散度量化得來的，而概率分布來自對應的參數集合上。本文中的設置由靜態擴展為動態版本，利用馬爾科夫鏈信息幾何來捕捉暫時的相互依賴關系。

論文地址：www.mdpi.com/1099-4300/17/4/2432

幾何學

將微分幾何擴展到概率單純形時，KL散度作為非測量連接。

熱力學

一項可以從不平衡的系統中提取的測量方法，使其達到平衡。

結語

由此可見，KL散度作為概率的概念之一，在多個領域都得到了應用。除了上述所介紹的領域外，KL散度最常用的領域還是統計學。除了上文所說的用處，在模型選擇上，它還是赤池信息量準則的基礎標準。