本文來自加州大學(xué)洛杉磯分校計(jì)算機(jī)科學(xué)專業(yè)的本科生OneRaynyDay，他喜歡用清晰易懂且不失幽默的方式講述機(jī)器學(xué)習(xí)概念，尤其是其中的數(shù)學(xué)概念。相比作者這個(gè)“數(shù)學(xué)怪胎”，小編能力有限，只能盡力去計(jì)算驗(yàn)證和補(bǔ)齊文中未介紹的概念。如果內(nèi)容有誤，歡迎在留言中指出。

蒙特卡洛是座賭城

目錄

簡介

蒙特卡洛動作值

初識蒙特卡洛

蒙特卡洛控制

Monte Carlo ES On-Policy：? -Greedy Policies Off-policy：重要性抽樣

Python里的On-Policy Model

在強(qiáng)化學(xué)習(xí)問題中，我們可以用馬爾可夫決策過程（MDP）和相關(guān)算法找出最優(yōu)行動值函數(shù) q?(s,a)和v?(s)，它通過策略迭代和值迭代找出最佳策略。

這是個(gè)好方法，可以解決強(qiáng)化學(xué)習(xí)中隨機(jī)動態(tài)系統(tǒng)中的許多問題，但它還有很多限制。比如，現(xiàn)實(shí)世界中是否真的存在那么多明確知道狀態(tài)轉(zhuǎn)移概率的問題？我們可以隨時(shí)隨地用MDP嗎？

那么，有沒有一種方法既能對一些復(fù)雜度過高的計(jì)算進(jìn)行近似求解，又能處理動態(tài)系統(tǒng)中的所有問題？

這就是我們今天要介紹的內(nèi)容——蒙特卡洛方法。

簡介

蒙特卡洛是摩納哥大公國的一座知名賭城，里面遍布輪盤賭、擲骰子和老虎機(jī)等游戲，類似的，蒙特卡洛方法的建模機(jī)制也基于隨機(jī)數(shù)和統(tǒng)計(jì)概率。

和一般動態(tài)規(guī)劃算法不同，蒙特卡洛方法（MC）以一個(gè)全新的視角來看待問題。簡而言之，它關(guān)注的是：我需要從環(huán)境中進(jìn)行多少次采樣，才能從不良策略中辨別出最優(yōu)策略？

論智注：關(guān)于動態(tài)規(guī)劃算法和MC的視角差異，我們可以舉這兩個(gè)例子：

問：1+1+1+1+1+1+1+1 =？ 答：（掰手指）8。 問：在上式后再+1呢？ 答：9！ 問：怎么這么快？ 答：因?yàn)?+1=9。 ——?jiǎng)討B(tài)規(guī)劃：記住求過的解來節(jié)省時(shí)間！

問：我有一個(gè)半徑為R的圓和一把豆子，怎么計(jì)算圓周率？ 答：在圓外套一個(gè)邊長為2R的正方形，往里面隨機(jī)扔豆子。 問：此話怎講？ 答：如果扔了N顆豆，落入圓里的豆子有n顆。N越大，n/N就越接近πR2/4R2。 ——MC：手工算完全比不過祖沖之，我好氣！

為了從數(shù)學(xué)角度解釋MC，這里我們先引入強(qiáng)化學(xué)習(xí)中的“return”（R），也就是“回報(bào)”概念，計(jì)算agent的長期預(yù)期收益（G）：

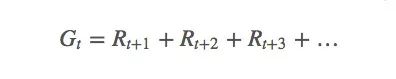
有時(shí)候，當(dāng)前策略的狀態(tài)概率在這個(gè)episode內(nèi)是非零的，它在之后連續(xù)多個(gè)episode里也是非零的，我們就要綜合考慮當(dāng)前回報(bào)和未來回報(bào)的重要程度。

這不難理解，強(qiáng)化學(xué)習(xí)的回報(bào)往往有一定滯后性。比如下圍棋時(shí)，當(dāng)前下的子可能目前看來沒有多大用處，但它在之后的局勢中可能會顯示出巨大的優(yōu)勢或劣勢，因此我們的圍棋agent需要考量長期回報(bào)。這個(gè)衡量標(biāo)準(zhǔn)就是折扣因子γ：

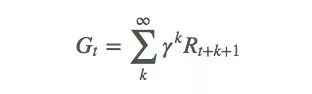
γ一般在[0,1]之間。當(dāng)γ=0時(shí)，只考慮當(dāng)前回報(bào)；當(dāng)γ=1時(shí)，均衡看待當(dāng)前回報(bào)和未來回報(bào)。

有了收益Gt和概率At，我們就能計(jì)算當(dāng)前策略下，狀態(tài)s的函數(shù)值V(s)：

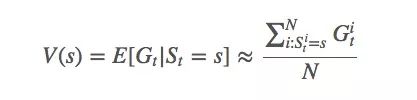
根據(jù)大數(shù)定律，當(dāng)N逼近∞時(shí)，我們可以得到確切的函數(shù)期望值。我們對第i次模擬進(jìn)行索引。可以發(fā)現(xiàn)，如果使用的是MDP（可以解決99%的強(qiáng)化學(xué)習(xí)問題），由于它有很強(qiáng)的馬爾可夫性，即確信系統(tǒng)下個(gè)狀態(tài)只與當(dāng)前狀態(tài)有關(guān)，與之前的信息無關(guān)：

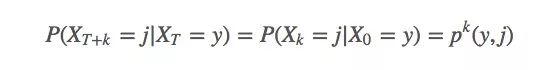
我們可以推導(dǎo)出這樣一個(gè)事實(shí)：t和期望值完全沒有關(guān)系。所以我們可以直接用Gs來表示從某個(gè)狀態(tài)開始的期望回報(bào)（將狀態(tài)前移到t = 0時(shí)）。

初識蒙特卡洛

計(jì)算值函數(shù)最經(jīng)典的方法是對狀態(tài)s的每個(gè)first visit進(jìn)行采樣，然后計(jì)算平均值，也就是first-visit MC prediction。下面是找到最優(yōu)V的算法：

pi = init_pi()

returns = defaultdict(list)

for i in range(NUM_ITER):

episode = generate_episode(pi) # (1)

G = np.zeros(|S|)

prev_reward = 0

for (state, reward) in reversed(episode):

reward += GAMMA * prev_reward

# backing up replaces s eventually,

# so we get first-visit reward.

G[s] = reward

prev_reward = reward

for state in STATES:

returns[state].append(state)

V = { state : np.mean(ret) for state, ret in returns.items() }

另一種方法則是every-visit MC prediction，即計(jì)算s的所有visit的平均值。雖然兩者有輕微不同，但同樣的，如果visit次數(shù)夠大，它們最后會收斂到相似值。

蒙特卡洛動作值

如果我們有一個(gè)完整的模型，我們只需知道當(dāng)前狀態(tài)值，就能選擇一個(gè)可以獲得最高回報(bào)的動作。但如果不知道模型信息呢？蒙特卡洛的特色是無需知道完整的環(huán)境知識，只需經(jīng)驗(yàn)就能學(xué)習(xí)。因此當(dāng)我們不知道什么動作會導(dǎo)致什么狀態(tài)，或者環(huán)境內(nèi)部會存在什么互動性時(shí)，我們用的是動作值q*，而不是MDP中的狀態(tài)值。

這就意味著我們估計(jì)的是qπ(s,a)，而不是vπ(s)，回報(bào)G[s]也應(yīng)該是G[s,a]。如果原來G的空間維數(shù)是S，現(xiàn)在就成了S×A，這是個(gè)很大的空間，但我們還是得繼續(xù)對其抽樣，以找出每個(gè)狀態(tài)動作元組（state?action pair）的預(yù)期回報(bào)。

正如上一節(jié)提到的，蒙特卡洛計(jì)算值函數(shù)的方法有兩種：first-visit MC和every-visit MC。因?yàn)樗阉骺臻g過大，如果策略過于貪婪，我們就無法遍歷每個(gè)state?action pair，做不到兼顧exploration和exploitation。關(guān)于這個(gè)問題的解決方法，我們會在下一節(jié)具體講述。

蒙特卡洛控制

我們先來回顧一下MDP的策略迭代方式：

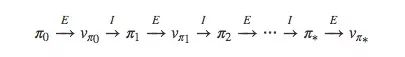
對于蒙特卡洛方法，它的迭代方式并沒有我們想象中的不同，也是先從π開始，然后是qπ0，再是π′……

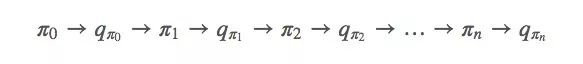
論智注：從π到q的過程代表的是一個(gè)完整的策略評估過程，而從q到π則代表一個(gè)完整的策略過程。其中策略評估過程會產(chǎn)生很多episode，得到很多接近真實(shí)函數(shù)的action-value函數(shù)。和vπ0一樣，雖然這里我們估計(jì)出的每個(gè)動作值都是一個(gè)近似值，但通過用值函數(shù)的近似值進(jìn)行迭代，經(jīng)過多輪迭代后，我們還是可以收斂到最優(yōu)策略。

既然qπ0和vπ0并沒有那么不同，MDP可以用動態(tài)規(guī)劃法求解，那么我們也可以繼續(xù)套用貝爾曼最優(yōu)性方程（Bellman optimality equation），即：

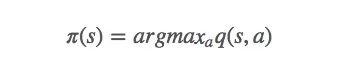
如果不理解，這里有一份中文介紹：增強(qiáng)學(xué)習(xí)（三）——MDP的動態(tài)規(guī)劃解法。

下面就是exploration vs. exploitation。

Monte Carlo ES

面對這么大一個(gè)搜索空間，一個(gè)補(bǔ)救方法是假定我們每個(gè)episode都會從一個(gè)特定的狀態(tài)開始，并采取特定的行動，也就是exploring start，然后從所有可能回報(bào)中抽樣。它背后的思想是認(rèn)定我們能從任意狀態(tài)開始，并在每個(gè)episode之初采取所有動作，同時(shí)策略評估過程可以利用無限個(gè)episode完成。這在很多情況下是不合常理的，但在環(huán)境未知問題中卻有奇效。

在實(shí)際操作中，我們只需在之前的代碼塊里添加如下內(nèi)容：

# Before (Start at some arbitrary s_0, a_0)

episode = generate_episode(pi)

# After (Start at some specific s, a)

episode = generate_episode(pi, s, a) # loop through s, a at every iteration.

On-Policy：? -Greedy策略

那么，如果我們不能假設(shè)自己能從任意的狀態(tài)開始并采取任意的動作呢？不再貪婪，不再存在無限個(gè)episode，我們是否還能擬合最優(yōu)策略？

這就是On-Policy的思想。所謂On-Policy，指的是評估、優(yōu)化現(xiàn)在正在做決策的那個(gè)策略；而off-policy改進(jìn)的則是和現(xiàn)在正在做決策的那個(gè)策略不同的策略。

因?yàn)槲覀円安辉儇澙贰保詈唵蔚姆椒ň褪怯忙?greedy：對于任何時(shí)刻t的執(zhí)行“探索”小概率ε<1，我們會有ε的概率會進(jìn)行exploration，有1-ε的概率會進(jìn)行exploitation。相比貪婪策略，?-Greedy隨機(jī)選擇策略（不貪婪）的概率是ε/|A(s)|。

現(xiàn)在的問題是，這是否會收斂到蒙特卡洛方法的最優(yōu)策略π*？——答案是會，但只是個(gè)近似值。

?-Greedy收斂

讓我們從q和一個(gè)?-greedy策略π′(s)開始：

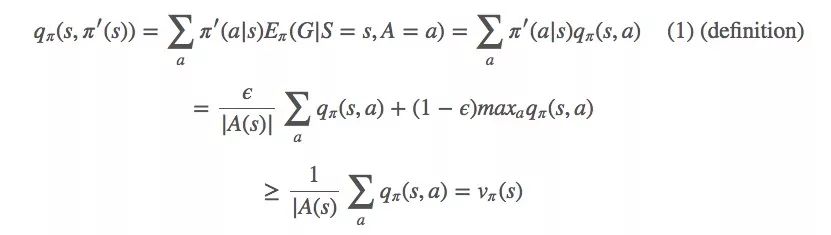
?-greedy策略像貪婪策略一樣對vπ做單調(diào)改進(jìn)。如果回到每一步細(xì)看，就是：

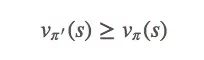
（1）

這是我們的收斂目標(biāo)。

這只是理論上的結(jié)果，它真的能擬合嗎？顯然不行，因?yàn)樽顑?yōu)策略是固定的，而我們選擇的策略是被迫隨機(jī)的，所以它不能保證收斂到π*——我們來重構(gòu)我們的問題：

假設(shè)我們不用概率ε在隨機(jī)選擇策略，而是無視規(guī)則，真正做到了完全隨機(jī)選擇策略，那么我們就能保證得到至少一個(gè)最優(yōu)策略。即，如果（1）里的等式成立，那么我們就有π=π'，因此vπ=vπ'，受環(huán)境約束，這時(shí)我們獲得的策略是隨機(jī)情況下最優(yōu)的。

Off-policy：重要性抽樣

Off-policy注釋

我們先來看一些定義：

π：目標(biāo)策略，我們希望能優(yōu)化這些策略已獲得最高回報(bào)；

b：動作策略，我們正在用b生成π之后會用到的各種數(shù)據(jù)；

π(a|s)>0?b(a|s)>0?a∈A：整體概念。

Off-policy策略通常涉及多個(gè)agent，其中一個(gè)agent一直在生成另一個(gè)agent試圖優(yōu)化的數(shù)據(jù)，我們分別稱它們?yōu)樾袨椴呗院湍繕?biāo)策略。就像神經(jīng)網(wǎng)絡(luò)比線性模型更“有趣”，同樣的，Off-policy策略一般也比On-Policy策略更好玩，也更強(qiáng)大。當(dāng)然，它也更容易出現(xiàn)高方差，更難收斂。

重要性采樣則是統(tǒng)計(jì)學(xué)中估計(jì)某一分布性質(zhì)時(shí)使用的一種方法。它在這里充當(dāng)?shù)慕巧腔卮稹敖o定Eb[G]，Eπ[G]是什么”？換句話說，就是我們?nèi)绾问褂脧腷抽樣得到的信息來確定π的預(yù)期回報(bào)？

直觀來看，如果b選了很多a，π也選了很多a，那b在π中應(yīng)該發(fā)揮著重要作用；相反地，如果b選了很多a，π并不總是跟著b選a，那b因a產(chǎn)生的狀態(tài)不會對π因a產(chǎn)生的狀態(tài)產(chǎn)生過大影響。

以上就是重要性采樣的基礎(chǔ)思想。給定從t到T的策略迭代軌跡(Si,Ai)Ti=t，策略π擬合這個(gè)軌跡的可能性是：

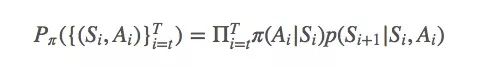
簡單地說，π和b之間的比率就是：

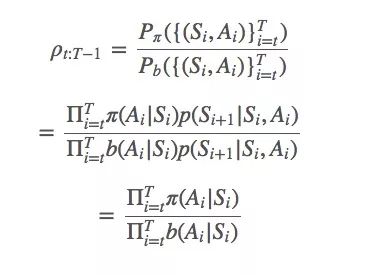
一般重要性采樣

現(xiàn)在我們有很多方法可以用ρt:T?1計(jì)算Eπ[G]的最優(yōu)解，比如一般重要性采樣（ordinary importance sampling）。設(shè)我們采樣了N個(gè)episode：

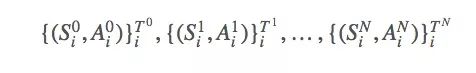
s的首次出現(xiàn)時(shí)間是：

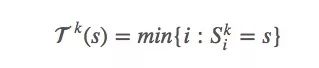
因?yàn)橐烙?jì)vπ(s)，所以我們可以用之前提到的first-visit方法計(jì)算均值來估計(jì)值函數(shù)。

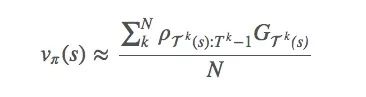
這里用first-visit只是為了簡便，我們也可以把它擴(kuò)展到every-visit。事實(shí)上，我們應(yīng)該結(jié)合不同方法來衡量每個(gè)episode的回報(bào)，因?yàn)槿绻心軘M合最優(yōu)策略的軌跡，我們應(yīng)該給它更多權(quán)重。

這種重要性抽樣方法是一種無偏差估計(jì)，它可能存在嚴(yán)重的方差問題。想想那個(gè)重要性比率，如果在第k輪的某個(gè)episode之中，ρT(s):Tk?1=1000，這就太大了，但它完全有可能存在。那這個(gè)1000會造成多大影響？如果我們只有一個(gè)episode，它的影響可想而知，但因?yàn)閺?qiáng)化學(xué)習(xí)任務(wù)往往很長，再加上里面有很多乘法計(jì)算，這個(gè)比例會存在爆炸和消失兩種結(jié)果。

加權(quán)重要性采樣

為了降低方差，一種可行的方法是加入權(quán)重來計(jì)算總和：

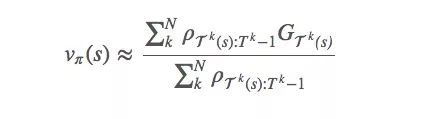
這被稱為加權(quán)重要性采樣（weighted importance sampling）。它是一個(gè)有偏差的估計(jì)（偏差趨于0），但與此同時(shí)方差降低了。如果是實(shí)踐，強(qiáng)烈建議加權(quán)！

增量式實(shí)現(xiàn)

蒙特卡洛預(yù)測方法也可以采用增量式的實(shí)現(xiàn)方式，假設(shè)我們使用上節(jié)中的加權(quán)重要性采樣，那么我們可以得到如下形式的一些抽樣算法：

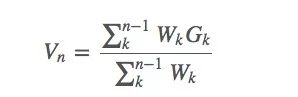
其中Wk是我們的權(quán)重。

假設(shè)我們有了估計(jì)值Vn和當(dāng)前獲得的回報(bào)Gn，要利用Vn與Gn來估計(jì) Vn+1，同時(shí)，我們用∑nkWk表示前幾輪回報(bào)的權(quán)重之和Cn。那么這個(gè)等式就是：

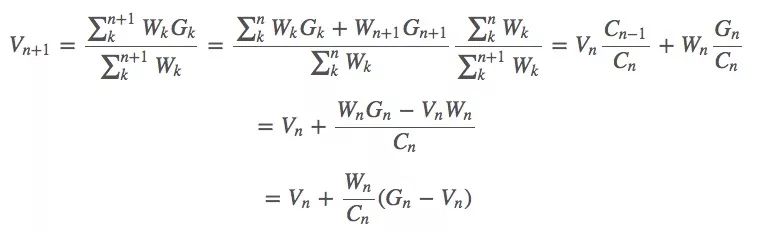
權(quán)重：Cn+1=Cn+Wn+1

現(xiàn)在，這個(gè)Vn就是我們的值函數(shù)，同樣的方法也適用于求動作值函數(shù)Qn。

在我們更新價(jià)函數(shù)的同時(shí)，我們也可以更新我們的策略π—— argmaxaQπ(s,a)。

注：這里涉及很多數(shù)學(xué)知識，但已經(jīng)很基礎(chǔ)了，確切地說，最前沿的也和這個(gè)非常接近。

下面還有針對折扣因子、獎(jiǎng)勵(lì)的抽樣簡介，具體請看原文，小編動不了了。

Python里的On-Policy Model

由于蒙特卡洛方法的代碼通常具有相似的結(jié)構(gòu)，作者已經(jīng)在python中創(chuàng)建了一個(gè)可以直接使用的蒙特卡洛模型類，感興趣的讀者可以在Github上找到代碼。

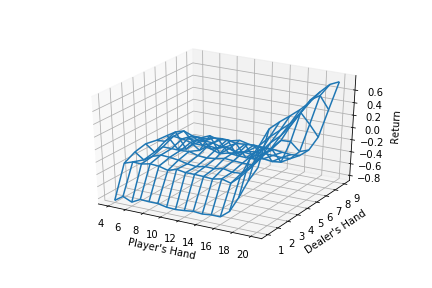
他還在原文中做了示例：用? -greedy policy解決Blackjack問題。

總而言之，蒙特卡洛方法利用episode的采樣學(xué)習(xí)最佳值函數(shù)和最佳策略，它無需建立對環(huán)境的充分認(rèn)知，在不符合馬爾可夫性時(shí)性能穩(wěn)定，是一種值得嘗試的好方法，也是新人接觸強(qiáng)化學(xué)習(xí)的一塊良好基石。

本文參考閱讀：

[1]增強(qiáng)學(xué)習(xí)（二）——馬爾可夫決策過程MDP：https://www.cnblogs.com/jinxulin/p/3517377.html

[2]增強(qiáng)學(xué)習(xí)（四）——蒙特卡羅方法(Monte Carlo Methods)：http://www.cnblogs.com/jinxulin/p/3560737.html

[3]算法-動態(tài)規(guī)劃 Dynamic Programming--從菜鳥到老鳥：https://blog.csdn.net/u013309870/article/details/75193592

[4]蒙特卡羅用于計(jì)算圓周率pi：http://gohom.win/2015/10/05/mc-forPI/

[5]蒙特卡洛方法 （Monte Carlo Method）：https://blog.csdn.net/coffee_cream/article/details/66972281