筆記1中我們利用 numpy 搭建了神經網絡最簡單的結構單元:感知機。筆記2將繼續學習如何手動搭建神經網絡。我們將學習如何利用 numpy 搭建一個含單隱層的神經網絡。單隱層顧名思義,即僅含一個隱藏層的神經網絡,抑或是成為兩層網絡。
繼續回顧一下搭建一個神經網絡的基本思路和步驟:
定義網絡結構(指定輸出層、隱藏層、輸出層的大小)
初始化模型參數
循環操作:執行前向傳播/計算損失/執行后向傳播/權值更新
定義網絡結構
假設 X 為神經網絡的輸入特征矩陣,y 為標簽向量。則含單隱層的神經網絡的結構如下所示:
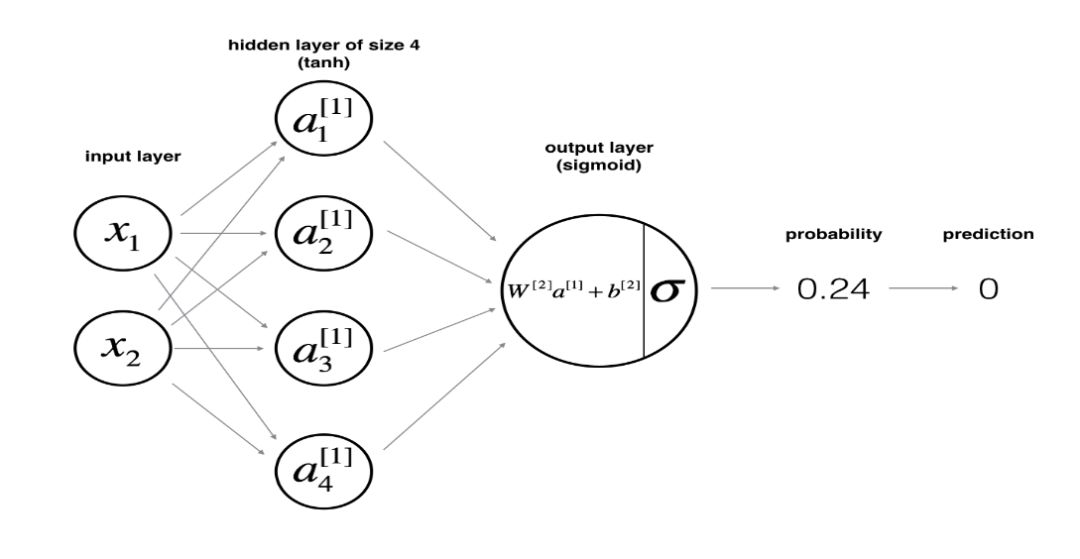
網絡結構的函數定義如下:
def layer_sizes(X, Y): n_x = X.shape[0] # size of input layer n_h = 4 # size of hidden layer n_y = Y.shape[0] # size of output layer return (n_x, n_h, n_y)
其中輸入層和輸出層的大小分別與 X 和 y 的 shape 有關。而隱層的大小可由我們手動指定。這里我們指定隱層的大小為4。
初始化模型參數
假設 W1 為輸入層到隱層的權重數組、b1 為輸入層到隱層的偏置數組;W2 為隱層到輸出層的權重數組,b2 為隱層到輸出層的偏置數組。于是我們定義參數初始化函數如下:
def initialize_parameters(n_x, n_h, n_y): W1 = np.random.randn(n_h, n_x)*0.01 b1 = np.zeros((n_h, 1)) W2 = np.random.randn(n_y, n_h)*0.01 b2 = np.zeros((n_y, 1)) assert (W1.shape == (n_h, n_x)) assert (b1.shape == (n_h, 1)) assert (W2.shape == (n_y, n_h)) assert (b2.shape == (n_y, 1)) parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2} return parameters
其中對權值的初始化我們利用了 numpy 中的生成隨機數的模塊 np.random.randn ,偏置的初始化則使用了 np.zero 模塊。通過設置一個字典進行封裝并返回包含初始化參數之后的結果。
前向傳播
在定義好網絡結構并初始化參數完成之后,就要開始執行神經網絡的訓練過程了。而訓練的第一步則是執行前向傳播計算。假設隱層的激活函數為 tanh 函數, 輸出層的激活函數為 sigmoid 函數。則前向傳播計算表示為:
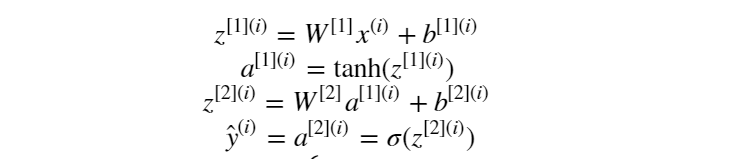
定義前向傳播計算函數為:
def forward_propagation(X, parameters): # Retrieve each parameter from the dictionary "parameters" W1 = parameters['W1'] b1 = parameters['b1'] W2 = parameters['W2'] b2 = parameters['b2'] # Implement Forward Propagation to calculate A2 (probabilities) Z1 = np.dot(W1, X) + b1 A1 = np.tanh(Z1) Z2 = np.dot(W2, Z1) + b2 A2 = sigmoid(Z2) assert(A2.shape == (1, X.shape[1])) cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2} return A2, cache
從參數初始化結果字典里取到各自的參數,然后執行一次前向傳播計算,將前向傳播計算的結果保存到 cache 這個字典中, 其中 A2 為經過 sigmoid 激活函數激活后的輸出層的結果。
計算當前訓練損失
前向傳播計算完成后我們需要確定以當前參數執行計算后的的輸出與標簽值之間的損失大小。與筆記1一樣,損失函數同樣選擇為交叉熵損失:
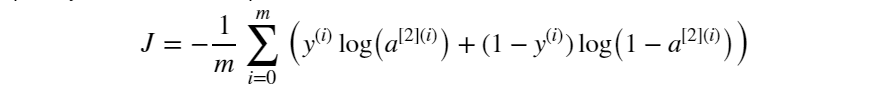
定義計算損失函數為:
def compute_cost(A2, Y, parameters): m = Y.shape[1] # number of example # Compute the cross-entropy cost logprobs = np.multiply(np.log(A2),Y) + np.multiply(np.log(1-A2), 1-Y) cost = -1/m * np.sum(logprobs) cost = np.squeeze(cost) # makes sure cost is the dimension we expect. assert(isinstance(cost, float)) return cost
執行反向傳播
當前向傳播和當前損失確定之后,就需要繼續執行反向傳播過程來調整權值了。中間涉及到各個參數的梯度計算,具體如下圖所示:

根據上述梯度計算公式定義反向傳播函數:
def backward_propagation(parameters, cache, X, Y): m = X.shape[1] # First, retrieve W1 and W2 from the dictionary "parameters". W1 = parameters['W1'] W2 = parameters['W2'] # Retrieve also A1 and A2 from dictionary "cache". A1 = cache['A1'] A2 = cache['A2'] # Backward propagation: calculate dW1, db1, dW2, db2. dZ2 = A2-Y dW2 = 1/m * np.dot(dZ2, A1.T) db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True) dZ1 = np.dot(W2.T, dZ2)*(1-np.power(A1, 2)) dW1 = 1/m * np.dot(dZ1, X.T) db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True) grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2} return grads
將各參數的求導計算結果放入字典 grad 進行返回。
這里需要提一下的是涉及到的關于數值優化方面的知識。在機器學習中,當所學問題有了具體的形式之后,機器學習就會形式化為一個求優化的問題。不論是梯度下降法、隨機梯度下降、牛頓法、擬牛頓法,抑或是 Adam 之類的高級的優化算法,這些都需要花時間掌握去掌握其數學原理。
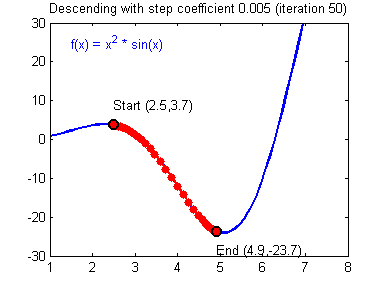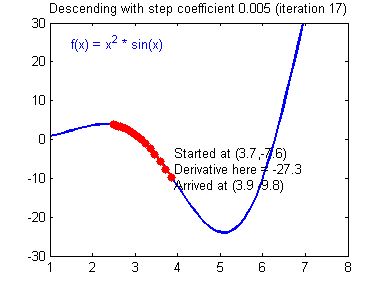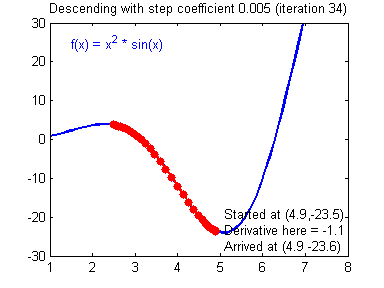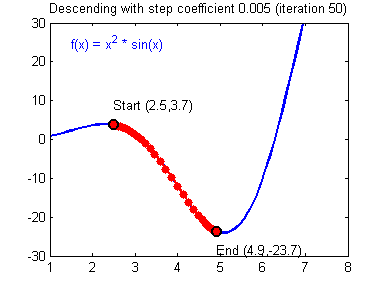
權值更新
迭代計算的最后一步就是根據反向傳播的結果來更新權值了,更新公式如下:

由該公式可以定義權值更新函數為:
def update_parameters(parameters, grads, learning_rate = 1.2): # Retrieve each parameter from the dictionary "parameters" W1 = parameters['W1'] b1 = parameters['b1'] W2 = parameters['W2'] b2 = parameters['b2'] # Retrieve each gradient from the dictionary "grads" dW1 = grads['dW1'] db1 = grads['db1'] dW2 = grads['dW2'] db2 = grads['db2'] # Update rule for each parameter W1 -= dW1 * learning_rate b1 -= db1 * learning_rate W2 -= dW2 * learning_rate b2 -= db2 * learning_rate parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2} return parameters
這樣,前向傳播-計算損失-反向傳播-權值更新的神經網絡訓練過程就算部署完成了。當前了,跟筆記1一樣,為了更加 pythonic 一點,我們也將各個模塊組合起來,定義一個神經網絡模型:
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False): np.random.seed(3) n_x = layer_sizes(X, Y)[0] n_y = layer_sizes(X, Y)[2] # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters". parameters = initialize_parameters(n_x, n_h, n_y) W1 = parameters['W1'] b1 = parameters['b1'] W2 = parameters['W2'] b2 = parameters['b2'] # Loop (gradient descent) for i in range(0, num_iterations): # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache". A2, cache = forward_propagation(X, parameters) # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost". cost = compute_cost(A2, Y, parameters) # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads". grads = backward_propagation(parameters, cache, X, Y) # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters". parameters = update_parameters(parameters, grads, learning_rate=1.2) # Print the cost every 1000 iterations if print_cost and i % 1000 == 0: print ("Cost after iteration %i: %f" %(i, cost)) return parameters
以上便是本節的主要內容,利用 numpy 手動搭建一個含單隱層的神經網路。從零開始寫起,打牢基礎,待到結構熟練,原理吃透,再去接觸一些主流的深度學習框架才是學習深度學習的最佳途徑。
-
神經網絡
+關注
關注
42文章
4812瀏覽量
103179 -
函數
+關注
關注
3文章
4376瀏覽量
64523
原文標題:深度學習筆記2:手寫一個單隱層的神經網絡
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
基于FPGA搭建神經網絡的步驟解析
【PYNQ-Z2試用體驗】基于PYNQ的神經網絡自動駕駛小車 - 項目規劃
【案例分享】ART神經網絡與SOM神經網絡
如何移植一個CNN神經網絡到FPGA中?
如何構建神經網絡?
如何使用Keras框架搭建一個小型的神經網絡多層感知器
輕量化神經網絡的相關資料下載
圖像預處理和改進神經網絡推理的簡要介紹
神經網絡移植到STM32的方法
如何使用numpy搭建一個卷積神經網絡詳細方法和程序概述
用Python從頭實現一個神經網絡來理解神經網絡的原理3






 搭建一個神經網絡的基本思路和步驟
搭建一個神經網絡的基本思路和步驟











評論