本文主要是回答激活函數的使用
我們認識的激活函數中sigmoid、ReLU等,今天就是要講解一下這些函數的一些性質
激活函數通常有一些性質:
非線性:當激活函數是線性的時候,一個兩層的神經網絡就可以基本逼近所有的函數,但是,如果激活函數是恒等激活函數的時候,就不滿足這個性質了,而且如果MLP使用的是恒等激活函數,那么其實整個網絡跟單層神經網絡是等價的
可微性:當優化方法是基于梯度的時候,這個性質是必須的
單調性:當激活函數是單調的時候,這個性質是必須的
f(x)≈x:當激活函數滿足這個性質的時候,如果參數的初始化是random的很小的值,那么神經網絡的訓練將會很高效;如果不滿足這個性質,那么就需要很用心的去設置初始值
輸出值的范圍:當激活函數輸出值是有限的時候,基于梯度的優化方法會更加穩定,因為特征的表示,當激活函數的輸出是無限的時候,模型訓練會更加的高效,不過在這種情況很小,一般需要一個更小的學習率
Sigmoid函數
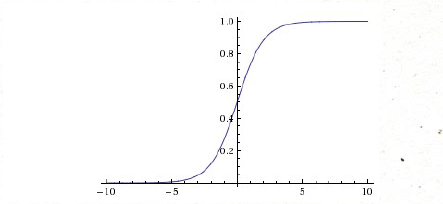
Sigmoid是常用的激活函數,它的數學形式是這樣,
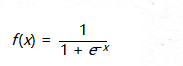
當如果是非常大的負數或者正數的時候,梯度非常小,接近為0,如果你的初始值是很大的話,大部分神經元都出在飽和的情況,會導致很難學習
還有就是Sigmoid的輸出,不是均值為0為的平均數,如果數據進入神經元的時候是正的(e.g.x>0elementwise inf=wTx+b),那么w計算出的梯度也會始終都是正的。
當然了,如果你是按batch去訓練,那么那個batch可能得到不同的信號,所以這個問題還是可以緩解一下的。因此,非0均值這個問題雖然會產生一些不好的影響
tanh
和Sigmoid函數很像,不同的是均值為0,實際上是Sigmoid的變形
數學形式
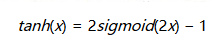
與Sigmoid不同的是,tanh是均值為0
ReLU
今年來,ReLU貌似用的很多
數學形式
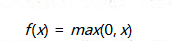
ReLU的優點
相比較其他的,ReLU的收斂速度會比其他的方法收斂速度快的多
ReLU只需要一個閾值就可以得到激活值,而不用去算一大堆復雜的運算
也有一個很不好的缺點:就是當非常大的梯度流過一個 ReLU 神經元,更新過參數之后,這個神經元再也不會對任何數據有激活現象了,所以我們在訓練的時候都需要設置一個比較合適的較小的學習率
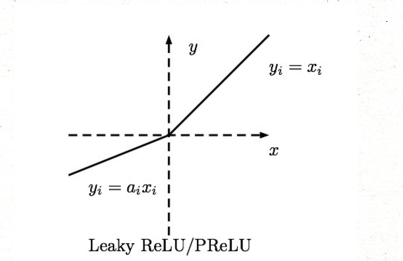
Leaky-ReLU、P-ReLU、R-ReLU
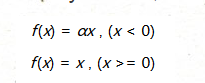
數學形式
f(x)=x,(x>=0)
這里的α是一個很小的常數。這樣,即修正了數據分布,又保留了一些負軸的值,使得負軸信息不會全部丟失
自己在寫神經網絡算法的時候還沒嘗試過這個激活函數,有興趣的同學可以試試效果
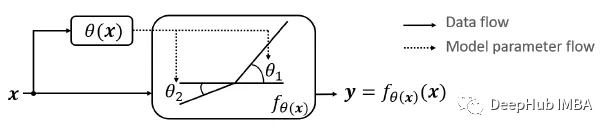
對于 Leaky ReLU 中的α,通常都是通過先驗知識人工賦值的。
然而可以觀察到,損失函數對α的導數我們是可以求得的,可不可以將它作為一個參數進行訓練呢?
不僅可以訓練,而且效果更好。
如何去選擇
目前業界人都比較流行ReLU,
-
神經網絡
+關注
關注
42文章
4811瀏覽量
103100 -
函數
+關注
關注
3文章
4374瀏覽量
64448
原文標題:BP神經網絡常用激活函數
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
多輸出Plateaued函數的密碼學性質
ReLU到Sinc的26種神經網絡激活函數可視化大盤點

13種神經網絡激活函數
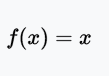





 激活函數中sigmoid、ReLU等函數的一些性質
激活函數中sigmoid、ReLU等函數的一些性質

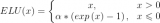










評論