IMM（交互式多模型）方法是Blom H．A．P．于1984年提出的。多模型方法主要用于特性隨時問變化系統(tǒng)的狀態(tài)估計，所以它特別適用于機動目標(biāo)的跟蹤。一種典型的例子就是對進行機動飛行的飛機的跟蹤。在IMM方法中，假定有有限多個目標(biāo)模型存在，每個模型對應(yīng)于不同機動輸入水平。在計算出各模型為正確的后驗概率之后，就可以通過對各模型正確的狀態(tài)估計加權(quán)求和來給出最終的目標(biāo)狀態(tài)估計，加權(quán)因子為模型正確的后驗概率。IMM估計器是已知最好的單次掃描狀態(tài)估計器，被廣泛應(yīng)用于各個領(lǐng)域，但還沒有應(yīng)用在機載警戒雷達的目標(biāo)跟蹤中。本文選取某警戒雷達產(chǎn)品的某幾條航跡用IMM方法進行濾波，把其濾波結(jié)果與目前實際工程中正在使用的．Kalman（Singer模型）濾波進行精度比較，實現(xiàn)模型的優(yōu)選。

1 算法流程

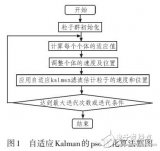
本次仿真過程主要分為數(shù)據(jù)的讀人、多模型濾波、數(shù)據(jù)的輸出3個部分。數(shù)據(jù)的讀入過程包括航跡同放后機體系數(shù)據(jù)讀人、航跡對應(yīng)的GPS數(shù)據(jù)的讀入以及把讀入的待處理數(shù)據(jù)進行坐標(biāo)系的轉(zhuǎn)換。多模型濾波過程即把上步中讀入并轉(zhuǎn)換成慣性系的數(shù)據(jù)分別在x、y、z軸進行多模型濾波。數(shù)據(jù)的輸出過程包括把多模型濾波后的軌跡輸出，并把此軌跡與實測的GPS（全球定位系統(tǒng)）軌跡以及用Kalman（Singer模型）濾波的軌跡進行比較，統(tǒng)計兩者的誤差大小。具體流程圖見圖l。

2 仿真輸人數(shù)據(jù)

本仿真隨機選取了某雷達實錄的兩條航跡，采用不同的模型組合對其進行濾波，分析對應(yīng)于不同的機動性采用哪兩種模型組合呵以最大限度地提高濾波的精度，并且以GPS測量數(shù)據(jù)為基準(zhǔn)，把其濾波結(jié)果與目前常用的Kalman（Singer模型）濾波精度進行比較，得出有參考價值的結(jié)論。

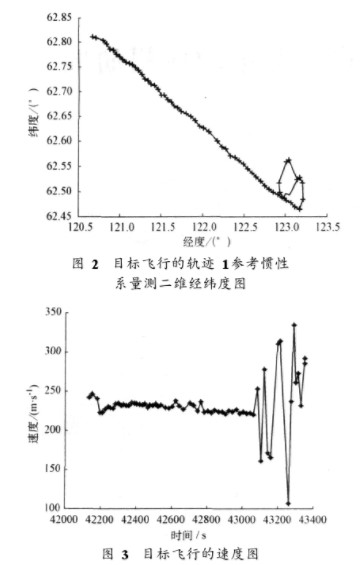
目標(biāo)軌跡l大致為：在時間42 138 s目標(biāo)從經(jīng)度120．667。、緯度40．250°勻速飛行到經(jīng)度123．172°、緯度62．465°，然后目標(biāo)在時間43 065 s處360。大轉(zhuǎn)彎，終點為經(jīng)度123．118°、緯度62．521°。目標(biāo)飛行的軌跡1參考慣性系量測二維經(jīng)緯度圖如圖2所示，目標(biāo)飛行的速度圖如圖3所示。

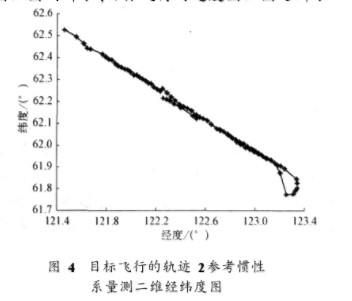
目標(biāo)軌跡2大致為：在時間39 163 s目標(biāo)在經(jīng)度121．456°、緯度65．525°處勻速飛行到經(jīng)度123．24l°、緯度61．89l°轉(zhuǎn)彎機動飛行到經(jīng)度l 22．25 l°、緯度62．215°。目標(biāo)飛行的軌跡2參考慣性系量測二維經(jīng)緯度圖如圖4所示，目標(biāo)飛行的速度圖如圖5所示。

3仿真輸出數(shù)據(jù)

3．1 航跡1

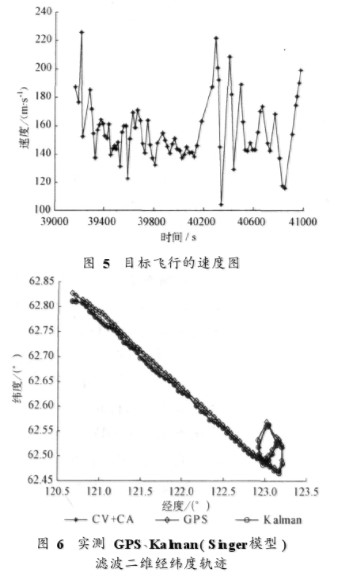
對航跡1分別采用CV模型與CA模型交互、CV模型與Singer‘模型交互、CV模型與“當(dāng)前”統(tǒng)計模型交互、Singer’模型與“當(dāng)前”統(tǒng)計模型交互，得到一組仿真圖和一組仿真數(shù)據(jù)。其中CV模型和cA模型組合仿真結(jié)果如下：CV模型交互CA模型濾波、實測GPs、Kalman（Singer模型）濾波二維經(jīng)緯度軌跡如圖6所示，CV模型交互CA模型濾波和Kalman（Singer模型）濾波的距離誤差如圖7所示，經(jīng)度誤差如圖8所示，緯度誤差如圖9所示。4種模型兩兩交互，共有6種有效模型組合。航跡1的6種模型組合濾波的距離誤差統(tǒng)計如表l所示，經(jīng)度誤差統(tǒng)計如表2所示，距離誤差統(tǒng)計如表3所示。航跡1用Kalman（Singer模型）濾波的距離誤差為64．453 8 m，經(jīng)度誤差為0．002 2°，緯度誤差為0．011 l°。

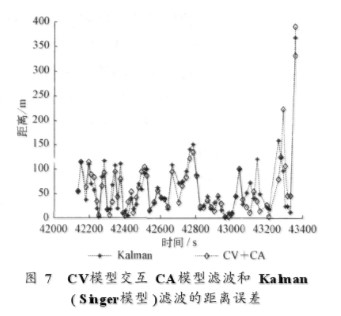
分析航跡l的仿真圖表可以看出，CV模型與CA模型交互、CV模型與Singer模型交互、CV模型與“當(dāng)前”統(tǒng)計模型交互濾波的距離誤差達到62．4 m，距離誤差比目前常用的Kalman（Singer模型）濾波的距離誤差小2 m左右。cA模型與Singer模型交互、CA模型與“當(dāng)前”統(tǒng)計模型交互的距離誤差都比Kalman（Singer模型）濾波的距離誤差大l m左右。Singer模型與“當(dāng)前”統(tǒng)計模型交互距離誤差比Kalman（Singer模型）濾波的距離誤差小l m左右。經(jīng)度和緯度的量綱很大，交互模型中包含CV模型的組合經(jīng)度可以提高0．000 l°，緯度可以提高0．000 9°。Singer模型與“當(dāng)前”統(tǒng)計模型交互的緯度提高O．000 2°，經(jīng)度精度沒有提高。由此可見，對于此條航跡，即目標(biāo)作了927 s的勻速運動后轉(zhuǎn)彎，CV模型與其余3種模型兩兩組合以及Singer模型與“當(dāng)前”統(tǒng)計模型的組合都提高了濾波的精度，其中以cV模型和“當(dāng)前”統(tǒng)計模型交互濾波提高的精度最高。

3．2 航跡2

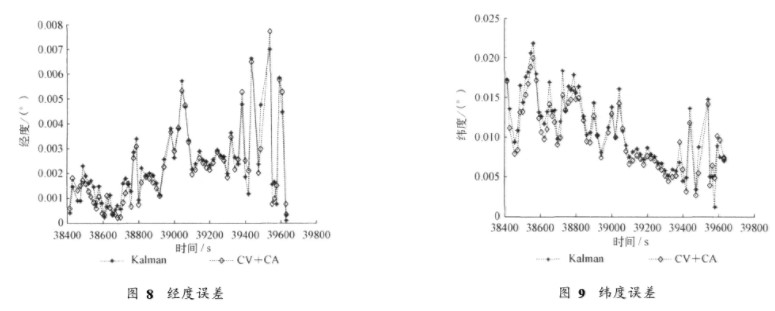
對航跡2也可分別采用cV模型與CA模型交互、CV模型與Singer模型交互、CV模型與“當(dāng)前”統(tǒng)計模型交互、Singer模型與“當(dāng)前”統(tǒng)計模型交互，得到一組仿真圖和一組仿真數(shù)據(jù)。其中，cA模型與“當(dāng)前”統(tǒng)計模型組合仿真結(jié)果如下：cA模型交互“當(dāng)前”統(tǒng)計模型濾波、實測GPS、Kalman（Singer模型）濾波二維經(jīng)緯度軌跡如圖10所示，CA模型交互“當(dāng)前”統(tǒng)計模型濾波和Kalman（Singer模型）濾波的距離誤差如圖l l所示，經(jīng)度誤差如圖12所示，緯度誤差如圖13所示。4種模型兩兩交互，共有6種有效模型組合。

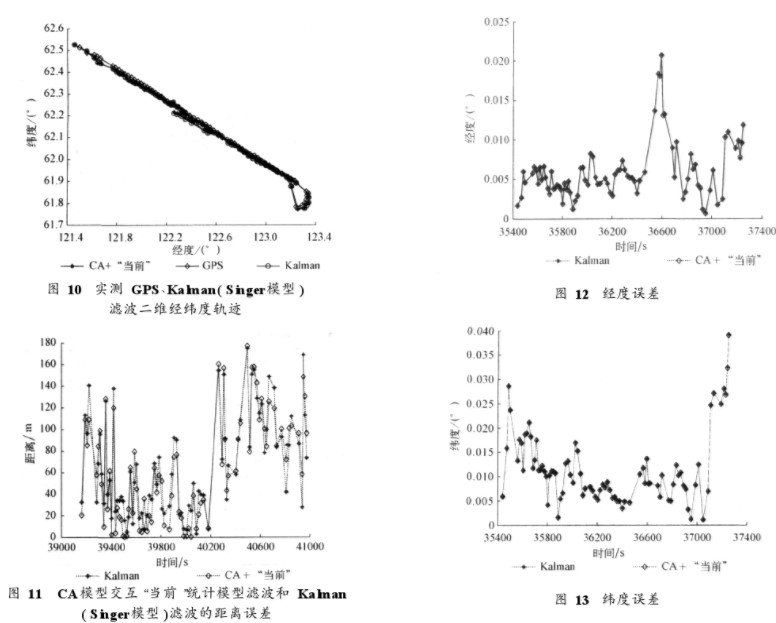
航跡2的6種模型組合濾波的距離誤差統(tǒng)計如表4所示，經(jīng)度誤差統(tǒng)計如表5所示，距離誤差統(tǒng)計如表6所示。航跡2用Kalman（Singer模型）濾波的距離誤差為103．600 3 m，經(jīng)度誤差為0．006 4°，緯度誤差為0．011 6°。

分析航跡2的仿真圖表可以看出，cV模型與CA模型交互、CV模型與Singer模型交互、CV模型與“當(dāng)前”統(tǒng)計模型交互濾波的距離誤差達到106．7 m，距離誤差比目前工程上使用的Kalman（Singer模型）濾波的距離誤差大3 m左右。CA模型和Singer模型交互距離誤差比Kalman（Singer模型）濾波的距離誤差小3 m左右，CA模型與“當(dāng)前”統(tǒng)計模型交互的距離誤差比Kalman（Singer模型）濾波的距離誤差小4 m左右。Singer模型與“當(dāng)前”統(tǒng)計模型交互距離誤差比Kal．

man（Singer模型）濾波的距離誤差小2 m左右。經(jīng)度和緯度的量綱很大，cA模型與“當(dāng)前”統(tǒng)計模型交互的經(jīng)度誤差和緯度誤差都減小了0．000 1°。由此可見，對于此條航跡，即目標(biāo)做了約l 037 s的勻速運動后做了約800 s的機動，CA模型與Singer模型組合、cA模型與“當(dāng)前”統(tǒng)計模型組合、Singer與“當(dāng)前”統(tǒng)計模型組合都提高r濾波的精度。包含CA模型的組合提高的精度較為明顯，其中以CA模型與“當(dāng)前”統(tǒng)計‘模型交互濾波提高的精度最高。

4 結(jié)論

本文用cV模型、cA模型、Singel’模型以及“當(dāng)前”統(tǒng)計模型兩兩交互的多模型算法來處理某警戒類雷達某天試飛的兩條航跡，把其仿真得出的一系列結(jié)果與目前工程中用來處理航跡濾波的Kalman（Singer模型）算法進行比較，得出了如下結(jié)淪：

a）Kalman（Singer模型）跟蹤簡單、計算方便，實時性強，在目標(biāo)跟蹤濾波中具有一定的意義。

b）在飛機做非機動運動或者做小機動運動時，用Kalman（Singer模型）來處理航跡可以達到較好的效果，但精度要比包含CV模型交互算法的精度低。

c）在飛機作高機動時，用多模型濾波算法進行跟蹤是有其優(yōu)越性的，可以在一定程度上提高濾波的精度。

d）多模型算法提高濾波精度的前提是目標(biāo)運動模型必須包含在多模型所設(shè)定的先驗?zāi)Ｐ图?，并且其假設(shè)的自相關(guān)時問常數(shù)要與機動運動自相關(guān)時間常數(shù)接近，這樣可以最大限度提高濾波的精度。

e）多模型算法中用Singer模型與“當(dāng)前”統(tǒng)計模型交互的適用范圍比較廣。Singer模型實質(zhì)是一種全局統(tǒng)計模型，而“當(dāng)前”統(tǒng)計模型是一種即時統(tǒng)計模型。因此，對應(yīng)于不同的機動情況，此兩種模型組合的濾波精度一定會比單模型的濾波精度高，但其精度比目標(biāo)運動模型包含在多模型所設(shè)定的先驗?zāi)Ｐ图袨V波的精度低。

5 結(jié)束語

IMM濾波算法是自適應(yīng)濾波算法，它的跟蹤效果比較平穩(wěn)，在目標(biāo)發(fā)生機動時不會出現(xiàn)較大的誤差。但多模型算法實質(zhì)上是一種折中的算法，它通常需要對目標(biāo)的機動特性做出合理的機動假設(shè)，選擇正確的先驗?zāi)Ｐ蛯Υ怂惴ǖ臑V波結(jié)果有比較大的影響。因此，模型的優(yōu)選問題還需要進一步研究，把交互式多模型算法運用在實際工程中還需要一定的時間。