編者按：Databricks數據科學主管Sean Owen討論了三種數據提供有歧義的結果的情況，以及因果關系如何幫助澄清數據的解讀。

相關和因果

相關性不等于因果。僅僅因為冰淇淋和美黑霜銷量同時上升或下降并不意味著兩者之間有什么因果關系。然而，人類的思考方式傾向于因果關系。你大概已經意識到這兩種商品的銷量均取決于夏季炎熱的天氣。那么，因果關系是一個什么樣的角色？

新入行的數據科學家可能有一個印象，因果關系是一個大家避而不談的話題。這是一個錯誤印象。我們使用數據決定“哪則廣告將導致更多點擊？”這樣的事情。已經有一個易用、開放工具的生態系統，可供我們基于數據建立模型，我們覺得這些模型可以回答關于成因和效果的問題。什么時候它們確實做到了這一點，什么時候我們誤以為它們做到了？

數據告訴我們什么，和我們認為數據告訴我們什么，這兩者之間存在著微妙的空隙，這正是困惑和錯誤的源泉。新入行的數據科學家，盡管配備了強大的建模工具，仍可能成為“未知的未知”的犧牲品，即使是在簡單的分析中也是如此。

本文將演示三種看起來簡單的情況，這些情況會產生驚人的歧義結果。劇透：在所有情形下，因果關系是澄清數據解讀必不可少的成分。包括概率圖模型和do-calculus在內的激動人心的工具，能夠讓我們基于數據和因果關系進行推理，得出強有力的結論。

兩條“最佳擬合”直線

考慮R內置的cars數據集。這個簡單的小數據集提供了不同車速的制動距離。假設低速情況下，兩者的關系是線性的。

再沒什么能比線性回歸更簡單了吧？距離是速度的函數：

同樣，速度也是距離的函數：

盡管看起來是同一件事，兩種說法，這兩種回歸會給出不同的最佳擬合直線。這兩條線不可能都是最佳的，那么哪一條才是最佳擬合直線，為什么？

如果你想親自驗證，可以查看、運行創建上面兩個圖形的代碼：https://trial.dominodatalab.com/u/srowen/causation/view/main.R

兩個最佳療法

下面的數據集可能看起來很熟悉。它顯示了腎結石的兩種療法的治愈率。

你也許注意到了上表的奇怪之處。總體而言，B療法的治愈率更高。然而，A療法在小結石上有著更高的治愈率，在小結石以外的情形（大結石）上也有著更高的治愈率。這怎么可能？你可以自己算一下。

許多人會馬上意識到這是辛普森悖論的一個典型例子。（這個例子取自辛普森悖論的維基頁面。）意識到這一點很重要。然而，意識到這一點并不能回答真正的問題：哪種療法更好？

這里，A療法更好。較大的腎結石更難治療，總體而言治愈率更低。在這些比較困難的情形下，更常應用A療法。雖然A療法實際上更好，但因為更常應用在困難情形下，總體治愈率被拉低了。結石大小是一個混淆變量，表格的橫行控制了結石大小。所以，控制所有像這樣的變量以避免出現悖論總不會錯吧？

考慮下面的數據：

這次是根據治療后病人的血酸分組。基于這些數據，哪種療法更好？為什么？

虛幻的相關性

最后，考慮R內置的mtcars數據集。它提供了20世界70年代的一些車型的統計數據，例如引擎汽缸容量、燃油效率、氣缸數量，等等。考慮drat（后輪軸減速比）和carb（化油器數量——現在的車不使用化油器，改用電子噴射系統）的相關性。

幾乎沒有相關性（r = -0.09）。這是有道理的，畢竟變速設計和引擎設計實際上是正交的。（我承認這不是一個最直觀的例子，但這是R語言內置的簡易數據集中最易懂的例子。）

然而，如果我們只考慮6缸或8缸引擎的車型：

有很清楚的正相關性（r = 0.52）。那么其他車型呢？

竟也有較小的正相關性（r = 0.22）。兩個變量在部分數據上相關，在剩余數據上也相關，但是在整體數據上卻不相關，怎么可能會這樣？

答案在因果關系之中

當然，這些問題都有答案。在第一個例子中，兩條不同的直線源自兩組不同的假定。距離 ~ 速度回歸意味著距離是速度的線性函數，加上高斯噪聲，直線最小化實際距離和預測距離的均方誤差。另一條直線最小化實際速度和預測速度的均方誤差。前者對應的假定是速度的不同導致了制動距離的不同，很有道理；后者暗示距離的不同導致了速度的不同，沒有意義。所以源自距離 ~ 速度的直線是正確的最佳擬合直線。不過，判定這一點需要數據以外的信息。

速度不同導致制動距離不同這一想法可以用一個（非常簡單的）有向圖表示：

類似地，在辛普森悖論的第二個例子中，血酸不再是混淆變量，而是中介變量。它并不導致選取哪種療法，反而是選取哪種療法導致了不同的血酸水平。將它作為控制變量等于移除了療法的主要效果。在這一情形下，B療法看起來要好一點，因為它導向更低的血酸，從而導向更好的結果（盡管A療法確實看起來有一些正面的次級效應）。

因此，辛普森悖論的原場景為：

而第二個場景為：

同樣，這里的“悖論”是可以解決的。關于因果關系的外部信息解決了“悖論”——兩個場景的解決方式不同！

第三個例子是伯克森悖論的一個例子。假定后輪軸減速比和化油器數目都影響汽缸數目（這里不展開討論，假定引擎設計上這一點成立），那么后輪軸減速比和化油器數量沒有相關性這一結論是正確的。控制汽缸數目創造了不存在的相關性，因為汽缸數目是同時和后輪軸減速比與化油器數量相關的“碰撞”變量。

同樣，數據沒有告訴我們這點；具備變量之間因果關系的知識才能得出這一結論。

概率圖模型和do-Calculus

我們上面繪制概率圖模型（PGM）有其目的。這些圖表達了成因-結果關系中的條件概率依賴的類型。盡管上述情形的概率圖很是微不足道，它們很容易變得很復雜。然而，不管簡單還是復雜，我們都可以通過分析概率圖檢測正確分析數據所需的變量之間的關系。

PGM是一個有趣的主題。（Coursera上有Daphne Koller開的課程。）理解因果關系的重要性，以及如何分析因果關系以正確解讀數據是數據科學家之旅必經的一步。

這類分析導向了一種可能更加激動人心的能力。假如一個變量取了不同的值，會發生什么？做出這方面的推理是有可能的。這一想法聽起來像是條件概率：給定今天的冰淇淋銷量很高（IC）這一條件，美黑霜的銷量很高（ST）的概率是多少？也就是，P(ST|IC)是多少？基于數據集，這很容易回答。如果兩者是正相關的，我們可以進一步期望P(IC|ST) > P(IC)——也就是說，當美黑霜的銷量很高的時候，冰淇淋的銷量很高的概率更大。

然而，如果我們提高了美黑霜的銷量（也許可以記作do(ST)），那么冰淇淋的銷量會增長嗎？很清楚，P(IC|do(ST))和P(IC|ST)不是一回事，因為我們不期望這兩者之間有什么因果聯系。

數據只提供了簡單的條件概率嗎？我們有可能演算數據中未曾發生的反事實概率，從而評判這些有關行動的論斷嗎？

令人驚喜的答案，是的，在因果模型和Judea Pearl提出的“do-calculus”的幫助下，這是有可能的。do-calculus是Pearl的新書The Book of Why的主題。這本書總結了因果思考的歷史，貝葉斯網絡，圖模型和Pearl自己對這一領域的顯著貢獻，在此高度推薦。

也許do-calculus最引人入勝的演示是這本書對吸煙致癌相關研究的回溯分析。據Pearl所述，吸煙致癌到底是通過肺部煙焦油囤積，還是因為未知的基因因素同時導致了喜歡吸煙和易得肺癌，對此人們曾有疑問。不幸的是，這一基因因素無法觀測，也不可能控制。畫出其中暗含的因果模型，就很容易做出推理。

即使在不能確定基因因素是否存在的情況下，還有可能回答“吸煙致癌”這樣的問題嗎？P(癌|do(吸煙)) > P(癌)嗎？

通過應用do-calculus的三條基本規則，這是有可能做到的，具體細節這里就不展開了（請看論文和書）。應用do-calculus規則之后，只涉及吸煙、煙焦油、癌癥的條件概率，這些都可以從現實數據集中得出：

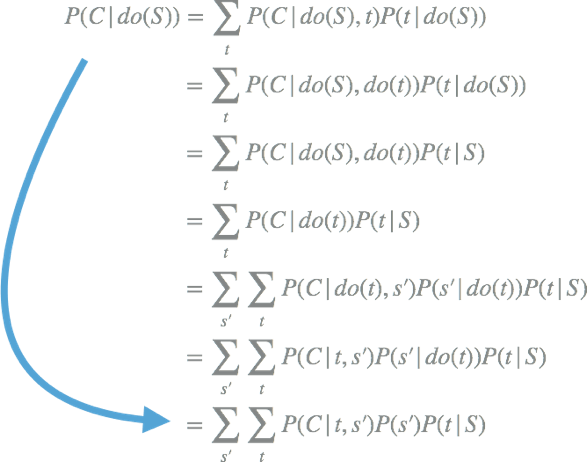
僅僅通過數據中的條件概率，即使在不知道是否存在未知混淆變量的情況下，就有可能知道是否吸煙導致患癌風險增加，

結語

有經驗的數據科學家不僅知道如何將工具作為黑箱使用，還知道模型和數據的正確解讀常常具有歧義，甚至違背直覺。避免常見誤區是資深從業者的標志。

幸運的是，許多這樣的悖論有著常見的來源，通過基于成因-效果網絡的推理，可以分析這些來源，從而解決這些悖論。概率圖模型和統計方法一樣重要。

再加上do-calculus，我們可以基于數據做出一些解讀和分析，對那些習慣相信無法僅僅從數據中得到因果或反事實結論的人來說，這些解讀和分析十分驚人！