對自動駕駛車輛的整體安全性和魯棒性來說,在穩(wěn)定操控范圍外的操縱能力相當重要。因此,本文提出了一種用于復(fù)雜軌跡自動漂移的控制器架構(gòu)。在不假設(shè)車輛工作在平衡點附近的情況下,設(shè)計了針對非特定路徑的控制器。提出了物理上有深刻意義的控制律:采用車輛航向角速度跟蹤路徑,橫擺角加速度用于鎮(zhèn)定質(zhì)心側(cè)偏角。通過非線性模型反演與下層輪速控制相結(jié)合,在大范圍工況下精確地實現(xiàn)所需求的狀態(tài)微分。在全尺寸車輛上進行的實車試驗表明,在不同曲率、速度和質(zhì)心側(cè)偏角下可以很好地跟蹤軌跡。
傳統(tǒng)車輛控制架構(gòu)中通常采用獨立的側(cè)向/縱向控制,并且假定車輛處于側(cè)滑動力學(xué)穩(wěn)定范圍內(nèi)。然而,超出車輛的操控極限時會產(chǎn)生強輸入耦合和橫擺/側(cè)滑不穩(wěn)定性,導(dǎo)致這種簡化方法失效。專業(yè)駕駛員在漂移中可以同時實現(xiàn)對車輛側(cè)滑和行駛路徑兩者的精確控制,盡管是完全在車輛穩(wěn)定性極限范圍外操縱的。自動駕駛漂移控制算法可以將車輛可用狀態(tài)空間擴展到極限范圍外,從而確保自動駕駛車輛最廣泛的機動范圍。
早期文獻中,Velenis[9]和Hindiyeh等人[4]分別通過仿真和實驗,研究了車輛狀態(tài)在漂移平衡點下的鎮(zhèn)定。因為在標準輸入下(轉(zhuǎn)角和驅(qū)動力矩)系統(tǒng)是欠驅(qū)動的,所以同時跟蹤路徑和鎮(zhèn)定質(zhì)心側(cè)偏角并不簡單。
最近的一些研究已經(jīng)在簡單的定圓試驗中證明了這一點。Werling等人[11]提出的控制器同時考慮了質(zhì)心側(cè)偏角鎮(zhèn)定和路徑跟蹤,而Goh等人[3]的策略則是明確的跟蹤路徑。但是由于在車輛建模和控制器設(shè)計時的進行了嚴格假設(shè),這些方法不能輕易地擴展到更復(fù)雜的軌跡。
已有文獻中,關(guān)于漂移的研究都使用了在大范圍內(nèi)精確的車輛模型。Ono[6]和Voser等人[10]使用了雙狀態(tài)單軌模型研究漂移的不穩(wěn)定動力學(xué)。也有學(xué)者將力作為直接輸入[3] [4]并且對轉(zhuǎn)向和油門延遲進行精確建模[11]的三狀態(tài)單軌模型用于試驗驗證控制器的設(shè)計。Velenis等人[9]基于線性化后的具有穩(wěn)態(tài)載荷轉(zhuǎn)移和車輪動力學(xué)的雙軌車輛模型,設(shè)計了線性二次型調(diào)節(jié)器。在運動方程的模型精度和可控性之間取得平衡,仍需進一步研究。
與這些方法相比,本文設(shè)計了一種用于處理復(fù)雜軌跡工況的自動漂移控制器。以道路曲線坐標系下的質(zhì)心側(cè)偏角誤差和側(cè)向位移誤差作為控制目標。首先在不需要假設(shè)特定的車輛模型或車輛狀態(tài)處于平衡點附近的情況下,推導(dǎo)出控制器設(shè)計所需的動力學(xué)模型。由此得到的控制律,用車輛狀態(tài)微分來表示,十分簡單直觀。利用漂移時產(chǎn)生的側(cè)偏和橫擺動力學(xué)解耦:直接采用車輛航向角速度跟蹤路徑,通過控制車輛橫擺角速度相對于航向角速度的快慢,可以同時鎮(zhèn)定質(zhì)心側(cè)偏角。
為了實現(xiàn)這一控制律,需要車輛模型將這些期望的狀態(tài)微分映射到輸入。通過非線性模型反演與下層的輪速控制相結(jié)合,實現(xiàn)復(fù)雜軌跡下大范圍工況的良好準確度,而不是依靠過于簡化的假設(shè)。在全尺寸測試車輛MARTY(圖1)上的試驗驗證了算法在曲率在1/7到1/20m間變化和速度在25km/h到45km/h間變化的軌跡以及-40°的質(zhì)心側(cè)偏角工況下的有效性。
圖1 自動漂移測試中的MARTY車輛
2試驗車輛與車輛模型
本節(jié)首先介紹了在曲線坐標系下的基于力輸入的單軌模型的運動方程,然后介紹了輪胎力模型。
2.1運動方程
2.1.1 路徑跟蹤狀態(tài)和動力學(xué)
車輛模型如圖2所示,有三個狀態(tài)變量:橫擺角速度r、速度V和質(zhì)心側(cè)偏角β。考慮路徑跟蹤后,引入了其他幾個狀態(tài)變量。車輛航向角是車輛速度矢量在給定的慣性坐標系的方向,的動力學(xué)方程:

圖2 參考路徑曲線坐標系下的三狀態(tài)單軌模型
利用曲線坐標系使車輛跟蹤參考軌跡,側(cè)向位移誤差e是車輛質(zhì)心到參考軌跡的最近點的距離,s是沿路徑到這個點的距離。參考航向角是s處路徑相對于慣性坐標系的正切角,航向角誤差 ,是車輛航向角與參考航向角之差。e的動力學(xué)方程表示為:
,是車輛航向角與參考航向角之差。e的動力學(xué)方程表示為:

進行一些簡化假設(shè):
 和
和 ,由于閉環(huán)控制中
,由于閉環(huán)控制中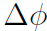 逐漸變小,因此假設(shè)合理。
逐漸變小,因此假設(shè)合理。
最后,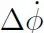 的動力學(xué)方程為
的動力學(xué)方程為

其中 是參考軌跡在s處的曲率。
是參考軌跡在s處的曲率。
2.1.2 車輛狀態(tài)和動力學(xué)
基于如圖2所示的單軌自行車模型進行非線性車輛模型反演,其中作用于車輛的力包括前軸側(cè)向力Fyf,后軸側(cè)向力Fyr和后軸縱向力Fxr,運動方程為:

其中δ為轉(zhuǎn)向角,a,b分別是前后軸到質(zhì)心的距離,m是車輛質(zhì)量。
2.2前軸輪胎力建模
前軸側(cè)向力Fyf采用Fiala刷子輪胎模型[2]表示,文獻[3] [4]中的漂移控制器中也采用了該模型。

其中Fz是輪胎垂向載荷,Cα是側(cè)偏剛度,α是側(cè)偏角,μ是輪胎附著系數(shù)。
2.3 后軸輪胎力建模
漂移時,整個后輪輪胎接地面處于完全滑動的狀態(tài)。假設(shè)各向同性摩擦系數(shù),側(cè)向力和縱向力受摩擦圓關(guān)系約束:

文獻[3] [4]控制算法設(shè)計時通過摩擦圓建立期望的后軸側(cè)向力Fyf與后軸縱向力Fxr映射關(guān)系,直接將后軸縱向力作為系統(tǒng)輸入并乘以輪胎半徑得到后軸轉(zhuǎn)矩需求。
該方法忽略了車輪動力學(xué),但當考慮更復(fù)雜軌跡工況時車輪動力學(xué)是相當重要的;Fxr不是真正的輸入,而是輪胎與路面滑移的結(jié)果。對于完全飽和的輪胎,力和滑移的關(guān)系可以以一種既簡單又有物理意義的方法進行建模:力大小為μFz,其方向與滑移速度矢量Vslip方向相反。定義這個方向為推力角γ,如圖3所示,改變Rω矢量的長度可以直接改變γ。幾何關(guān)系為:

其中R是輪胎半徑,ω是輪速,Vtravelx和Vtravely分別是車輛在輪胎處速度的縱向和側(cè)向分量。
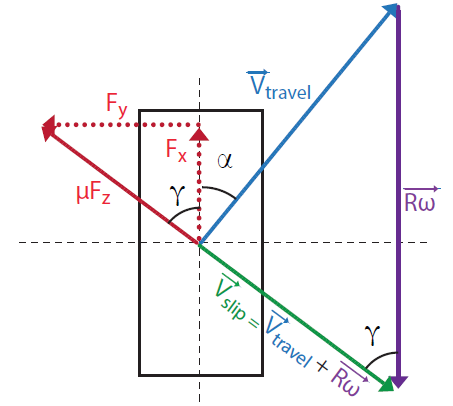
圖3 滑移輪胎的速度和力矢量
值得注意的是在完全飽和狀態(tài)下,這個關(guān)系同刷子輪胎模型[7]和簡化魔術(shù)公式輪胎模型[1]表達是一致的。系統(tǒng)的控制輸入,在車輪動力學(xué)ω中表達為:

其中Iω是車輪-輪胎-傳動系統(tǒng)的轉(zhuǎn)動慣量,τ為實際轉(zhuǎn)矩。
3控制器設(shè)計
3.1概述
控制器的任務(wù)是利用轉(zhuǎn)向角和后軸驅(qū)動力矩跟蹤給定路徑和期望質(zhì)心側(cè)偏角。因此選擇了側(cè)向位移誤差e和質(zhì)心側(cè)偏角β作為控制變量。
控制器的總體結(jié)構(gòu)如圖4所示,在第一部分,基于e和β的期望穩(wěn)定動力學(xué),得到期望的航向角速度 和綜合橫擺角速度rsyn,對rsyn閉環(huán)得到期望的橫擺角加速度
和綜合橫擺角速度rsyn,對rsyn閉環(huán)得到期望的橫擺角加速度 。
。
第二部分,通過非線性車輛動力學(xué)模型反演將 和
和 轉(zhuǎn)化為轉(zhuǎn)向角δ和期望的推力角γdes。然后將推力角映射到期望的輪速ωdes。最終,對ωdes閉環(huán)得到驅(qū)動力矩τ。
轉(zhuǎn)化為轉(zhuǎn)向角δ和期望的推力角γdes。然后將推力角映射到期望的輪速ωdes。最終,對ωdes閉環(huán)得到驅(qū)動力矩τ。

圖4控制器架構(gòu)框圖
3.2 誤差動力學(xué)
3.2.1 路徑跟蹤
航向角速度 直接用于跟蹤路徑。側(cè)向位移誤差e的期望二階動力學(xué)方程為:
直接用于跟蹤路徑。側(cè)向位移誤差e的期望二階動力學(xué)方程為:
 得到期望的
得到期望的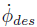 :
:

3.2.2 鎮(zhèn)定質(zhì)心側(cè)偏角
然后,與 相關(guān)的車輛橫擺角速度,用于鎮(zhèn)定質(zhì)心側(cè)偏角。質(zhì)心側(cè)偏角跟蹤誤差
相關(guān)的車輛橫擺角速度,用于鎮(zhèn)定質(zhì)心側(cè)偏角。質(zhì)心側(cè)偏角跟蹤誤差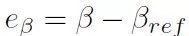 的期望一階動力學(xué)方程:
的期望一階動力學(xué)方程:

與文獻[3] [4]中方法類似,基于綜合輸入橫擺角速度rsyn計算得到期望的 ,這些方法進行了
,這些方法進行了 的穩(wěn)態(tài)近似,然后,由于對航向角速度
的穩(wěn)態(tài)近似,然后,由于對航向角速度 有明確的控制,使用期望的航向角速度
有明確的控制,使用期望的航向角速度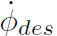 替代。
替代。

對橫擺角速度跟蹤誤差 的一階求導(dǎo),得到期望的橫擺角加速度
的一階求導(dǎo),得到期望的橫擺角加速度 。
。

其中 是綜合橫擺角速度的微分,可以近似表達為:
是綜合橫擺角速度的微分,可以近似表達為:

其中 是參考軌跡的橫擺角加速度。
是參考軌跡的橫擺角加速度。
3.3 非線性模型反演
通過公式(5)中非線性單軌車輛模型反演,將期望 變換為轉(zhuǎn)向角和后軸縱向力/推力角。
變換為轉(zhuǎn)向角和后軸縱向力/推力角。
圖5中是一組比較有代表性的狀態(tài)微分間曲面關(guān)系。投影到 平面(圖6),可以看到曲面發(fā)生折疊即部分區(qū)域?qū)τ诮o定組合有兩個解。這樣把曲面分成較大的“上”表面和較小的“下”表面;分界線如圖5、6、7中紅線所示。
平面(圖6),可以看到曲面發(fā)生折疊即部分區(qū)域?qū)τ诮o定組合有兩個解。這樣把曲面分成較大的“上”表面和較小的“下”表面;分界線如圖5、6、7中紅線所示。
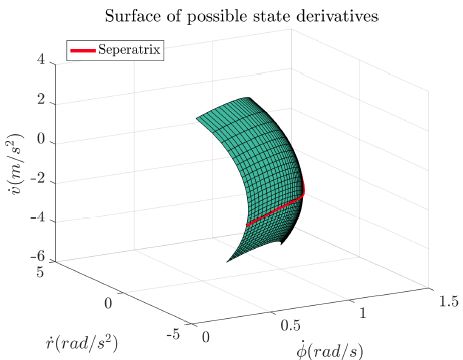
圖5橫擺角速度為53.9°/s,車速為9.35m/s,質(zhì)心側(cè)偏角為-40°時車輛狀態(tài)微分間三維圖

圖6沿車速微分等高線的橫擺角加速度vs航向角速度

圖7沿橫擺角加速度等高線的航向角速度vs車速微分
通常來講,僅有小部分 空間是位于下表面的,因此模型反演可以在上表面約束下得到1對1的映射關(guān)系,并以簡單的方式確保執(zhí)行器指令的連續(xù)性。另外值得注意的是,上表面通常包括狀態(tài)組合
空間是位于下表面的,因此模型反演可以在上表面約束下得到1對1的映射關(guān)系,并以簡單的方式確保執(zhí)行器指令的連續(xù)性。另外值得注意的是,上表面通常包括狀態(tài)組合 ,如圖7所示,在跟蹤準平衡軌跡時能實現(xiàn)此狀態(tài)微分空間。
,如圖7所示,在跟蹤準平衡軌跡時能實現(xiàn)此狀態(tài)微分空間。
需求的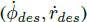 有可能落到可行域外。對控制器中初始時刻和試驗中產(chǎn)生的這種情況進行簡單處理。
有可能落到可行域外。對控制器中初始時刻和試驗中產(chǎn)生的這種情況進行簡單處理。 的值受到
的值受到 可行域的飽和約束,然后計算
可行域的飽和約束,然后計算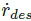 。得到的
。得到的 沿
沿 線投影到可行域內(nèi)。所提出策略中不穩(wěn)定的橫擺/側(cè)偏動力學(xué)控制優(yōu)先級高于側(cè)向位移誤差控制。
線投影到可行域內(nèi)。所提出策略中不穩(wěn)定的橫擺/側(cè)偏動力學(xué)控制優(yōu)先級高于側(cè)向位移誤差控制。
3.4 輪速控制
根據(jù)非線性模型反演得到的后軸縱向力/推力角,進而根據(jù)公式(8)中的力-滑移關(guān)系得到期望輪速。基于簡化的動態(tài)面控制[3]跟蹤期望輪速ωdes。

其中 是期望輪速在時間常數(shù)為
是期望輪速在時間常數(shù)為 的一階濾波后得到的,利用期望后軸縱向力
的一階濾波后得到的,利用期望后軸縱向力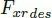 計算前饋力矩。
計算前饋力矩。
因為MARTY測試車輛后輪獨立可控且機械上解耦,分別對左右后輪進行控制。令左后輪和右后輪的推力角分別為 ,得到期望的左右輪和右后輪輪速
,得到期望的左右輪和右后輪輪速 和
和 ,其中d為車輛輪距,單輪的期望縱向力基于穩(wěn)態(tài)載荷轉(zhuǎn)移的假設(shè)得到:
,其中d為車輛輪距,單輪的期望縱向力基于穩(wěn)態(tài)載荷轉(zhuǎn)移的假設(shè)得到:

其中 為發(fā)生在后軸的載荷轉(zhuǎn)移的經(jīng)驗值,h為質(zhì)心高度。
為發(fā)生在后軸的載荷轉(zhuǎn)移的經(jīng)驗值,h為質(zhì)心高度。
4試驗驗證
在曲率在1/7到1/20間變化和速度在25km/h到45km/h間變化的復(fù)雜軌跡以及-40°的參考質(zhì)心側(cè)偏角下試驗驗證了算法的有效性。
4.1測試方法
試驗在如圖1所示的試驗平臺MARTY上進行。MARTY由1981 DMC Delorean改裝而來,配備有線控轉(zhuǎn)向和可獨立驅(qū)動左右后輪的電驅(qū)動系統(tǒng)。車輛狀態(tài)信息通過集成的RTK-GPS/IMU得到,更新頻率為250Hz。在上位機實時運行的控制算法的運算頻率也為250Hz。
在參考軌跡的起始點和末端分別增加簡單的進入和退出回旋線,用于文獻[5]相似的基礎(chǔ)路徑跟蹤控制器使得車輛跟蹤此路徑。漂移控制器在s=57m時介入,在s=463m時退出。控制器參數(shù)和車輛參數(shù)如表1所示。

表1控制器參數(shù)和車輛參數(shù)
4.2軌跡規(guī)劃
參考文獻[5]方法,軌跡是由不穩(wěn)定漂移平衡點序列構(gòu)成的。首先,選取期望曲率 和質(zhì)心側(cè)偏角
和質(zhì)心側(cè)偏角 ,其是關(guān)于路徑距離s的函數(shù)。對于參考軌跡中每個點,將
,其是關(guān)于路徑距離s的函數(shù)。對于參考軌跡中每個點,將 和
和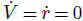 代入運動方程求解得到參考軌跡
代入運動方程求解得到參考軌跡 值,參考質(zhì)心側(cè)偏角
值,參考質(zhì)心側(cè)偏角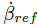 近似表示為
近似表示為 。
。
選取的配置文件曲率從1/7到1/20m間變化,參考質(zhì)心側(cè)偏角為-40°,得到平衡速度在25km/h到45km/h之間的軌跡。
圖8軌跡曲率與參考質(zhì)心側(cè)偏角配置
4.3試驗結(jié)果
控制算法較好地跟蹤了參考軌跡,表現(xiàn)出良好的側(cè)向位移誤差和質(zhì)心側(cè)偏角跟蹤效果。
如圖9所示,車輛的實際路徑與參考路徑十分接近,圖10給出了側(cè)向位移誤差與路徑距離的關(guān)系:其均方根誤差為0.18m,最大偏差為-0.36m。
車輛處于期望質(zhì)心側(cè)偏角-40°附近狀態(tài)時,達到了上述良好路徑跟蹤性能。圖11給出了測量的車輛狀態(tài),可以看出質(zhì)心側(cè)偏角跟蹤效果較好:均方根誤差為2.4°,最大偏差僅為-6.1°。閉環(huán)下速度也與軌跡參考速度十分接近,既說明了車速穩(wěn)定又說明了用于規(guī)劃的模型比較準確。除了在漂移起始時刻,測量的橫擺角速度也可以很好地跟蹤參考橫擺角速度。
最后值得注意的是,因為在較大的狀態(tài)范圍內(nèi)進行非線性模型反演,會產(chǎn)生較大范圍的輸入-最明顯的例子是控制算法在圖6測試時達到了65°。
圖9試驗中測量路徑vs參考路徑
圖10試驗中路徑跟蹤性能
圖11試驗中車輛狀態(tài)vs路徑距離
圖12試驗中轉(zhuǎn)向角和推力角輸入
5結(jié)論
本文設(shè)計了針對復(fù)雜軌跡的自動駕駛漂移控制器。控制器由車輛狀態(tài)微分推導(dǎo)得到,并且沒有涉及到特定的車輛模型。航向角速度用于跟蹤曲線坐標系下的側(cè)向位移誤差,然后控制相對于航向角速度的橫擺角速度從而控制質(zhì)心側(cè)偏角。
為了得到車輛狀態(tài)微分到執(zhí)行器輸入的映射關(guān)系,進行非線性模型反演和簡單的輪速閉環(huán)控制。試驗驗證了在曲率在1/7到1/20間變化和速度在25km/h到45km/h間變化的復(fù)雜軌跡以及-40°的參考質(zhì)心側(cè)偏角工況下的有效性。
對復(fù)雜軌跡下漂移平衡點的路徑跟蹤和質(zhì)心側(cè)偏角鎮(zhèn)定研究,保證了自動駕駛車輛在需要的情況下能夠在開環(huán)穩(wěn)定極限外操縱。未來的研究將進一步考慮在未進行準平衡假設(shè)下實現(xiàn)軌跡規(guī)劃和跟蹤,解決車輛狀態(tài)快速變化的問題。
-
控制器
+關(guān)注
關(guān)注
114文章
16998瀏覽量
183183 -
自動駕駛
+關(guān)注
關(guān)注
788文章
14226瀏覽量
169770
原文標題:復(fù)雜軌跡工況下的自動漂移控制
文章出處:【微信號:IV_Technology,微信公眾號:智車科技】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
什么是閃存控制器架構(gòu)?
分享一種微型步進電機驅(qū)動控制器
一種嵌入式運動控制器的實現(xiàn)

一種點對點高速通信控制器的設(shè)計與實現(xiàn)
一種簡化PID模糊控制器的研究與設(shè)計
一種面向連續(xù)軌跡的動態(tài)前瞻算法

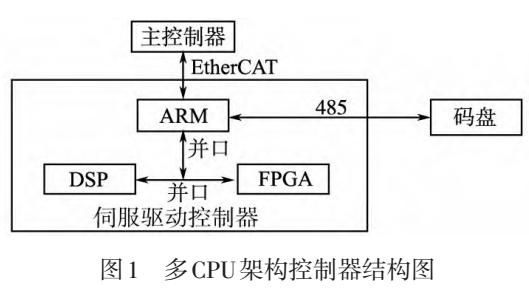
基于多CPU架構(gòu)伺服驅(qū)動控制器的研究
一種基于風(fēng)險軌跡與復(fù)雜網(wǎng)絡(luò)的缺陷定位方法

一種用于小功率開關(guān)變換器的數(shù)字PWM控制器和電流估計器

【深度解析】ZMC300E EtherCAT主站控制器實現(xiàn)復(fù)雜的運動軌跡規(guī)劃原理及應(yīng)用






 一種用于復(fù)雜軌跡自動漂移的控制器架構(gòu)
一種用于復(fù)雜軌跡自動漂移的控制器架構(gòu)










評論