前不久，史上最快的超大數相乘方法轟動業界。近日，借由這個思路，谷歌一名軟件工程師提出了另一種優化方式，使得量子版“遞歸”算法或將成為可能！

上個月，兩位研究人員發現的史上最快的超大數相乘方法，在業界掀起了不小的風波，有望破解存在了近半個世紀的數學難題。

而就在前幾日，著名科普網站QuantaMagazine發表了一篇文章稱，另一種新乘法運算方式為量子計算機打開了一扇新大門。

文章地址：

https://www.quantamagazine.org/a-new-approach-to-multiplication-opens-the-door-to-better-quantum-computers-20190424/

這篇論文作者是Google AI Quantum的軟件工程師Craig Gidney，于4月15日將文章《漸近有效的量子Karatsuba乘法》發表于arXiv。

論文地址：

https://arxiv.org/pdf/1904.07356.pdf

論文作者

在他的新論文中，Gidney描述了一種實現Karatsuba乘法的量子方法，這種方法不會產生巨大的內存開銷。他沒有先生成中間值，再得到最終值，而是使用一種稱為“尾調用優化”(tail call optimization)的方法來直接將輸入變為輸出。這使得算法可以避免創建量子計算機永遠無法丟棄的中間信息。

Gidney希望他的方法能夠使許多經典的遞歸算法適應量子計算機。目前，量子計算機還很初級，幾乎不能進行個位數乘法。但起碼有一個算法已經準備好了，只要它們的設計繼續改進，它們將能夠做更多的事情。

數學處處充滿驚喜：大數乘法世紀難題或將破解，又有益于量子計算

先來思考一下這么一個問題：

我9歲的時候，我家有了一臺新電腦。這臺電腦在各方面都比我們的舊電腦好，除了一點：它不能運行我最喜歡的賽車游戲。我記得我當時就想，如果一臺漂亮的新電腦不能運行我最喜歡的程序，那它還有什么意義呢?

同樣的問題也適用于量子計算機。理論上，量子計算機可以做經典計算機所能做的所有事情。然而，在實踐中，量子計算機的量子性質使它基本上不可能有效地運行一些最重要的經典算法。

而這又是什么原因呢？

我們知道，一臺經典計算機能做加法，它就能做乘法，而后可以處理許許多多更加復雜的信息。而量子計算機卻可能連非常基本的運算也難以做到，其間原因就是——無法做到“選擇性遺忘”。

“選擇性遺忘”就好比：一個2G的內存條實際上的容量或許只有1.95G。但對于量子計算機，它只能含淚說道：“臣妾做不到哇！”

而在Gidney的論文中所討論的乘法算法利用了一項發現，這是數千年來乘法領域的首次進步。傳統的小學乘法方法中，位數是n的兩個數字相乘需要n2步。幾千年來，數學家們一直認為沒有更有效的方法了。

但是，正如我們最近在《極限速度！10 億位超級大整數相乘僅需 30 秒，半個世紀的猜測終被證明》一文中所報道的，1960年，一位名叫阿納托利·卡拉蘇巴(Anatoly Karatsuba)的數學家發現了一種更快乘法方法。

他的方法是把長數字分成較短的數。例如，假如要將兩個8位的數字相乘，首先要將每個8位數字拆分為兩個4位的數，然后將每個4位數拆分為兩個兩位數。然后對所有兩位數進行計算，最后將結果重組，就是最終的乘積。對于涉及大數的乘法， Karatsuba的方法比小學法的步驟要少得多。

如何快速地將兩個大數相乘(Lucy Reading-Ikkanda/Quanta Magazine)

數千年來，將兩個n位的數字相乘，需要n2個步驟。1960年，俄羅斯數學家Anatoly Karatsuba提出了一種更好的方法。

比如，在25×63這個算式中，使用小學乘法方法需要4個單位數乘法步驟，并將4步所得的積相加，才能得到最后的結果。

同樣的算式使用Karatsuba的方法，只需要做3次乘法，以及少量的加法操作和移位操作。

隨著數字位數的增加，Karatsuba方法可以重復使用，將大的數字分割成較小的數字，從而節省更多的單位數乘法操作。

類似“尾調用優化”，量子版“遞歸算法”或將實現！

經典計算機運行Karatsuba方法時，它會隨著運行進行而刪除信息。例如，在將兩位數重組為四位數之后，它會忘記之前的兩位數，只關心四位數本身。經典的Karatsuba方法就像登山者在上山的路上脫下裝備一樣——不需要一路攜帶所有東西時，你可以走得更快。

但量子計算機無法隨時“脫下”信息。

量子計算機通過操縱量子比特系統來執行計算。“這些量子比特彼此交織或糾纏。這種糾纏使量子計算機擁有巨大的能量——量子計算機利用了所有量子比特之間存在的復雜關系，而不只是以單個比特存儲信息。因此，對于某些特定的問題，量子計算機可以具有經典計算機指數級倍數的處理能力。

量子糾纏，看似荒謬的超距感應

但是使量子計算機強大的這種特性也使它們變得脆弱。因為量子比特糾纏在一起，你不可能在不影響其他量子比特的情況下改變其中的一些量子比特。這使得不可能像經典計算機那樣有選擇地刪除信息。扔掉某些量子比特就像剪斷蜘蛛網上的某幾股線——即使只“咔嚓”一下也可能導致整個蛛網分崩離析。

保留信息的這種要求使得難以創建“遞歸”算法的量子版本，因為“遞歸”意味著它們會反饋給自身。遞歸算法在計算機科學中有很廣泛的應用，但為了達到最佳效果，它們要求計算機在每一步都要丟棄信息。沒有這種能力，計算很快就會變得不切實際。布里斯托爾大學(University of Bristol)量子信息科學家Ashley Montanaro說，“如果每次進行一項操作都會存儲信息，那么空間的大小就會隨著操作的數量而變化。”任何機器都會很快耗盡內存。

Gidney的工作在保持O(nlg3)門集程度(gate complexity)的同時，提高了量子計算機上從O1到O2的Karatsuba乘法的空間復雜度。他通過確保遞歸調用可以將其輸出直接添加到輸出寄存器的子部分來實現此目的。這避免了存儲和不計算中間結果的需求。

他使用Q#的跟蹤模擬器實現并測試了他的算法，并獲得具體的計數。

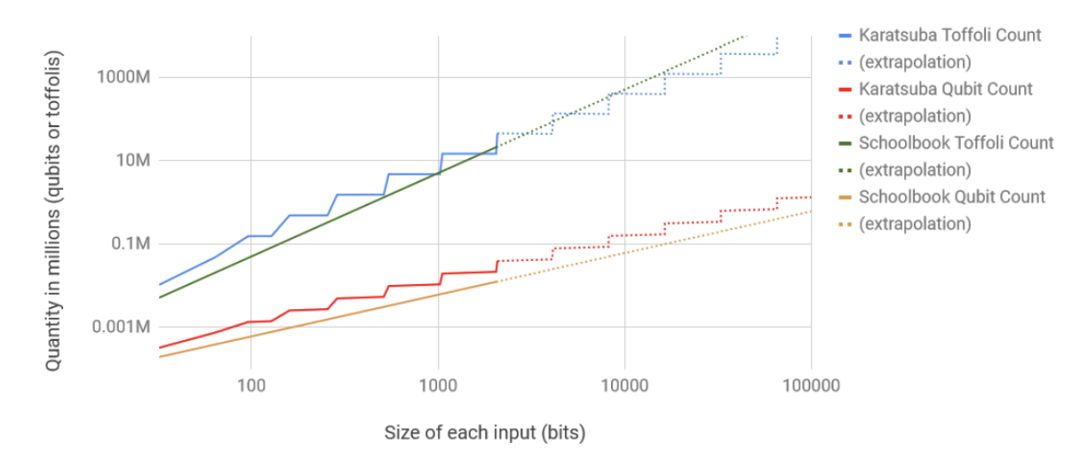
針對各種輸入尺寸的Karatsuba乘法和教科書乘法的Q＃implementation所使用的Toffoli gate和量子位數的雙對數坐標圖

值得注意的是，在作者的實現中，Karatsuba乘法比教科書乘法更高效的交叉點(約10000位)比現代RSA密鑰的大小(2048到8192位)更大，這表明Shor算法在實踐中應該更傾向于使用簡單的乘法。

不過，這篇論文關注的是漸近參數，而不是試圖優化常數因子。論文還忽略了一些重要的實際考慮，比如為了讓量子比特相互作用而將量子比特相互routing的成本。

此外，作者分析的情況(兩個量子整數的乘法)不同于Shor算法中的情況(一個量子整數與一個經典整數的受控模乘法)。因此，對于Karatsuba乘法在Shor算法中的實際應用，作者并沒有得出任何結論。

他表示，這種類似于經典尾調用優化的優化應該適用于各種遞歸量子算法。但在Gidney發表這篇論文之前，還不清楚是否有可能對這類算法進行改造，讓量子計算機也能運行。

Gidney希望他的新技術能讓量子計算機實現這類算法，而到目前為止，這類算法在量子計算機中使用似乎是緩慢而復雜的。