神經(jīng)網(wǎng)絡(luò)的初始化是訓(xùn)練流程的重要基礎(chǔ)環(huán)節(jié),會對模型的性能、收斂性、收斂速度等產(chǎn)生重要的影響。本文是deeplearning.ai的一篇技術(shù)博客,文章指出,對初始化值的大小選取不當(dāng), 可能造成梯度爆炸或梯度消失等問題,并提出了針對性的解決方法。
初始化會對深度神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練時間和收斂性產(chǎn)生重大影響。簡單的初始化方法可以加速訓(xùn)練,但使用這些方法需要注意小心常見的陷阱。本文將解釋如何有效地對神經(jīng)網(wǎng)絡(luò)參數(shù)進(jìn)行初始化。
有效的初始化對構(gòu)建模型至關(guān)重要
要構(gòu)建機器學(xué)習(xí)算法,通常要定義一個體系結(jié)構(gòu)(例如邏輯回歸,支持向量機,神經(jīng)網(wǎng)絡(luò))并對其進(jìn)行訓(xùn)練來學(xué)習(xí)參數(shù)。下面是訓(xùn)練神經(jīng)網(wǎng)絡(luò)的一些常見流程:
初始化參數(shù)
選擇優(yōu)化算法
然后重復(fù)以下步驟:
1、向前傳播輸入
2、計算成本函數(shù)
3、使用反向傳播計算與參數(shù)相關(guān)的成本梯度
4、根據(jù)優(yōu)化算法,利用梯度更新每個參數(shù)
然后,給定一個新的數(shù)據(jù)點,使用模型來預(yù)測其類型。
初始化值太大太小會導(dǎo)致梯度爆炸或梯度消失
初始化這一步對于模型的最終性能至關(guān)重要,需要采用正確的方法。比如對于下面的三層神經(jīng)網(wǎng)絡(luò)。可以嘗試使用不同的方法初始化此網(wǎng)絡(luò),并觀察對學(xué)習(xí)的影響。

在優(yōu)化循環(huán)的每次迭代(前向,成本,后向,更新)中,我們觀察到當(dāng)從輸出層向輸入層移動時,反向傳播的梯度要么被放大,要么被最小化。
假設(shè)所有激活函數(shù)都是線性的(恒等函數(shù))。 則輸出激活為:

其中 L=10 ,且W[1]、W[2]…W[L-1]都是2*2矩陣,因為從第1層到L-1層都是2個神經(jīng)元,接收2個輸入。為了方便分析,如果假設(shè)W[1]=W[2]=…=W[L-1]=W,那么輸出預(yù)測為

如果初始化值太大或太小會造成什么結(jié)果?
情況1:初始化值過大會導(dǎo)致梯度爆炸
如果每個權(quán)重的初始化值都比單位矩陣稍大,即:

可簡化表示為

且a[l]的值隨l值呈指數(shù)級增長。當(dāng)這些激活用于向后傳播時,會導(dǎo)致梯度爆炸。也就是說,與參數(shù)相關(guān)的成本梯度太大。 這導(dǎo)致成本圍繞其最小值振蕩。

初始化值太大導(dǎo)致成本圍繞其最小值震蕩
情況2:初始化值過小會導(dǎo)致梯度消失
類似地,如果每個權(quán)重的初始化值都比單位矩陣稍小,即:

可簡化表示為

且a[l]的值隨l值減少呈指數(shù)級下降。當(dāng)這些激活用于后向傳播時,可能會導(dǎo)致梯度消失。也就是說,與參數(shù)相關(guān)的成本梯度太小。這會導(dǎo)致成本在達(dá)到最小值之前收斂。

初始化值太小導(dǎo)致模型過早收斂
總而言之,使用大小不合適的值對權(quán)重進(jìn)行將導(dǎo)致神經(jīng)網(wǎng)絡(luò)的發(fā)散或訓(xùn)練速度下降。 雖然我們用的是簡單的對稱權(quán)重矩陣來說明梯度爆炸/消失的問題,但這一現(xiàn)象可以推廣到任何不合適的初始化值。
如何確定合適的初始化值
為了防止以上問題的出現(xiàn),我們可以堅持以下經(jīng)驗原則:
1.激活的平均值應(yīng)為零。
2.激活的方差應(yīng)該在每一層保持不變。
在這兩個假設(shè)下,反向傳播的梯度信號不應(yīng)該在任何層中乘以太小或太大的值。梯度應(yīng)該可以移動到輸入層,而不會爆炸或消失。
更具體地說,對于層l,其前向傳播是:

我們想讓下式成立:

確保均值為零,并保持每層輸入方差值不變,可以保證信號不會爆炸或消失。該方法既適用于前向傳播(用于激活),也適用于向后傳播(用于關(guān)于激活的成本梯度)。這里建議使用Xavier初始化(或其派生初始化方法),對于每個層l,有:

層l中的所有權(quán)重均自正態(tài)分布中隨機挑選,其中均值μ=0,方差E= 1/( n[l?1]),其中n[l?1]是第l-1層網(wǎng)絡(luò)中的神經(jīng)元數(shù)量。偏差已初始化為零。
下圖說明了Xavier初始化對五層全連接神經(jīng)網(wǎng)絡(luò)的影響。數(shù)據(jù)集為MNIST中選取的10000個手寫數(shù)字,分類結(jié)果的紅色方框表示錯誤分類,藍(lán)色表示正確分類。
結(jié)果顯示,Xavier初始化的模型性能顯著高于uniform和標(biāo)準(zhǔn)正態(tài)分布(從上至下分別為uniform、標(biāo)準(zhǔn)正態(tài)分布、Xavier)。



結(jié)論
在實踐中,使用Xavier初始化的機器學(xué)習(xí)工程師會將權(quán)重初始化為N(0,1/( n[l?1]))或N(0,2/(n[l-1]+n[1])),其中后一個分布的方差是n[l-1]和n[1]的調(diào)和平均。
Xavier初始化可以與tanh激活一起使用。此外,還有大量其他初始化方法。 例如,如果你正在使用ReLU,則通常的初始化是He初始化,其初始化權(quán)重通過乘以Xavier初始化的方差2來初始化。 雖然這種初始化證明稍微復(fù)雜一些,但其思路與tanh是相同的。
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4811瀏覽量
103066 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4374瀏覽量
64427 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8497瀏覽量
134245
原文標(biāo)題:一文看懂神經(jīng)網(wǎng)絡(luò)初始化!吳恩達(dá)Deeplearning.ai最新干貨
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
MATLAB神經(jīng)網(wǎng)絡(luò)工具箱函數(shù)
【案例分享】基于BP算法的前饋神經(jīng)網(wǎng)絡(luò)
改善深層神經(jīng)網(wǎng)絡(luò)--超參數(shù)優(yōu)化、batch正則化和程序框架 學(xué)習(xí)總結(jié)
怎么解決人工神經(jīng)網(wǎng)絡(luò)并行數(shù)據(jù)處理的問題
基于BP神經(jīng)網(wǎng)絡(luò)的PID控制
卷積神經(jīng)網(wǎng)絡(luò)模型發(fā)展及應(yīng)用
如何進(jìn)行高效的時序圖神經(jīng)網(wǎng)絡(luò)的訓(xùn)練
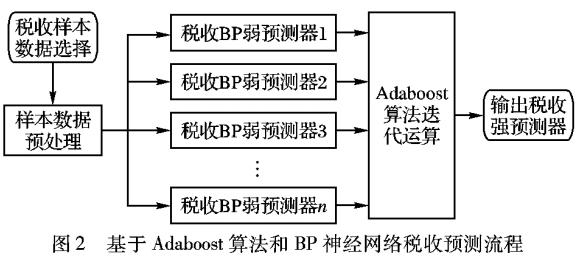
BP神經(jīng)網(wǎng)絡(luò)的稅收預(yù)測
神經(jīng)網(wǎng)絡(luò)是在許多用例中提供了精確狀態(tài)的機器學(xué)習(xí)算法

教大家怎么選擇神經(jīng)網(wǎng)絡(luò)的超參數(shù)
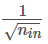





 如何有效地對神經(jīng)網(wǎng)絡(luò)參數(shù)進(jìn)行初始化
如何有效地對神經(jīng)網(wǎng)絡(luò)參數(shù)進(jìn)行初始化











評論