并行RLC電路與我們在前一個教程中看到的串聯(lián)電路完全相反,盡管前面的一些概念和方程仍然適用。
然而,并行RLC電路的分析在數(shù)學(xué)上可能比串聯(lián)RLC電路更困難,因此在本教程中關(guān)于并行RLC電路,本教程中僅假設(shè)純組件使事情變得簡單。
這次代替電路元件的共用電流,所有施加的電壓都是共同的,所以我們需要找到通過每個元件的各個支路電流。使用類似于DC并聯(lián)電路的電路的電流來計(jì)算并聯(lián)RLC電路的總阻抗Z,此時的差異是使用導(dǎo)納而不是阻抗。考慮下面的并行RLC電路。
并行RLC電路
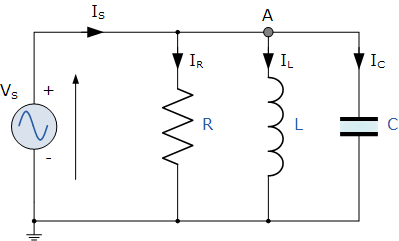
在上面的并行中在RLC電路中,我們可以看到電源電壓V S 對所有三個元件都是通用的,而電源電流I S 由三部分組成。流經(jīng)電阻器的電流I R ,流過電感器的電流I L 和通過電容器的電流I C 。
但是流過每個分支的電流以及每個元件的電流將彼此不同并且與電源電流I S 不同。從電源汲取的總電流不是三個獨(dú)立分支電流的數(shù)學(xué)和,而是它們的矢量和。
與RLC系列電路一樣,我們可以使用相量或矢量方法解決這個電路,但是這個時間矢量圖將電壓作為其參考,其中三個電流矢量相對于電壓繪制。并聯(lián)RLC電路的相量圖是通過將每個元件的三個單獨(dú)的相量組合在一起并矢量地添加電流而產(chǎn)生的。
由于電路兩端的電壓對所有三個電路元件都是通用的,我們可以使用這個作為參考矢量,其三個電流矢量以相應(yīng)的角度相對于此繪制。得到的向量 I S 是通過將兩個向量加在一起得到的, I L 和 I C 然后將此總和添加到剩余的矢量 I R 。在 V 和 I S 之間獲得的最終角度將是電路相位角,如下所示。
相量圖并行RLC電路
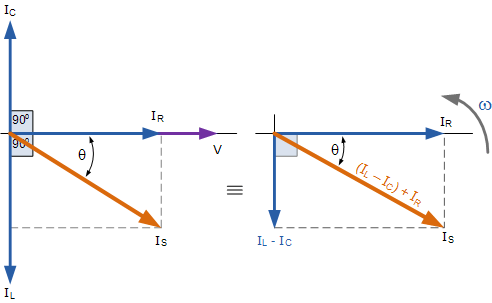
我們可以從右上方的相量圖中看到當(dāng)前矢量產(chǎn)生一個矩形三角形,包括斜邊 I S ,水平軸 I R 和垂直軸 I L -I C 希望您會注意到,這會形成當(dāng)前三角形,因此我們可以使用畢達(dá)哥拉斯定理當(dāng)前三角形以數(shù)學(xué)方式獲得沿x軸和y軸的分支電流的大小,然后確定這些分量的總電流I S ,如圖所示。
當(dāng)前三角形對于并聯(lián)RLC電路
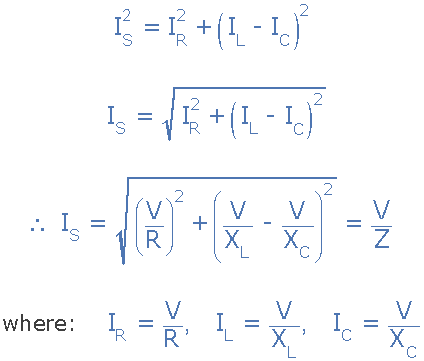
由于電路兩端的電壓對所有三個電路元件都是通用的,因此電流通過每個麩皮ch可以使用Kirchoff的Current Law(KCL)找到。基爾霍夫的現(xiàn)行定律或結(jié)法規(guī)定“進(jìn)入結(jié)點(diǎn)或節(jié)點(diǎn)的總電流與離開該節(jié)點(diǎn)的電流完全相同”,因此進(jìn)出節(jié)點(diǎn)“A”的電流如下:
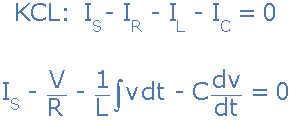
取導(dǎo)數(shù),用 C 除以上式并重新排列給出以下二 - 電路電流的等式。它成為二階方程,因?yàn)殡娐分杏袃蓚€電抗元件,電感和電容。
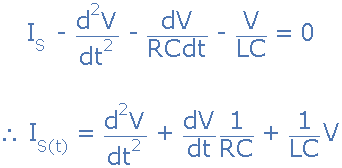
在這種類型的交流電路中對電流的反對由三個部分組成: X L X C 和 R ,這三個值的組合給出了電路阻抗, Z 。我們從上面知道,并聯(lián)RLC電路的所有組件中的電壓具有相同的幅度和相位。然后,每個元件的阻抗也可以根據(jù)流過的電流和每個元件的電壓進(jìn)行數(shù)學(xué)描述。
并聯(lián)RLC電路的阻抗
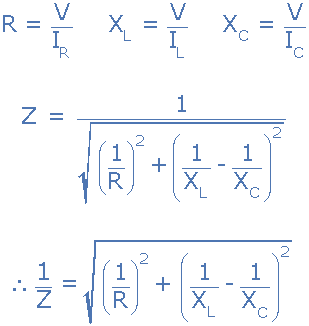
您會注意到,并聯(lián)RLC電路的最終公式為每個并聯(lián)支路產(chǎn)生復(fù)阻抗,因?yàn)槊總€元件都成為阻抗的倒數(shù),( 1 / Z )阻抗的倒數(shù)被稱為導(dǎo)納。
在并聯(lián)交流電路中,使用導(dǎo)納更方便,符號( Y )用于解決復(fù)雜的分支阻抗,特別是當(dāng)涉及兩個或多個并聯(lián)分支阻抗時(有助于數(shù)學(xué)運(yùn)算)。通過添加并行導(dǎo)納可以簡單地找到電路的總導(dǎo)納。那么電路的總阻抗 Z T 因此如圖所示 1 / Y T Siemens。 / p>
并行RLC電路的導(dǎo)納
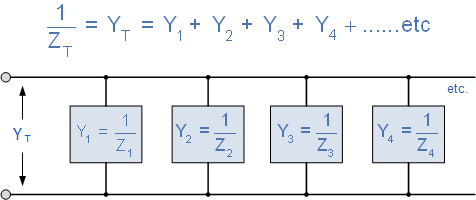
新的準(zhǔn)入單位是 Siemens ,縮寫為 S ,(舊單位mho的?,歐姆相反)。導(dǎo)納在并行分支中加在一起,而阻抗在串聯(lián)分支中加在一起。但是,如果我們可以得到阻抗的倒數(shù),我們也可以得到電阻和電抗的倒數(shù),因?yàn)樽杩褂蓛蓚€分量組成, R 和 X 。然后將電阻的倒數(shù)稱為電導(dǎo),電抗的倒數(shù)稱為電阻。
電導(dǎo),導(dǎo)納和電納
用于電導(dǎo),導(dǎo)納和電納的單位都是相同的,即西門子(S),也可以認(rèn)為是互惠的歐姆或歐姆 -1 ,但用于每個元素的符號是不同的,在純組件中,它的給出如下:
導(dǎo)納(Y):
導(dǎo)納是阻抗的倒數(shù), Z ,并給出符號 Y 。在交流電路中,導(dǎo)納定義為在施加電壓時考慮到電壓和電流之間的相位差,由電阻和電抗組成的電路允許電流流動的容易程度。
并聯(lián)電路是相量電流與相量電壓的比值,導(dǎo)納的角度與阻抗的角度相反。
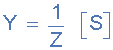
電導(dǎo)(G):
電導(dǎo)是電阻的倒數(shù), R 并給出符號 G 。電導(dǎo)定義為當(dāng)施加AC或DC電壓時電阻器(或一組電阻器)允許電流流動的容易程度。
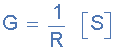
接受(B):
接受是...的倒數(shù)一個純電抗, X ,并給出符號 B 。在交流電路中,電納被定義為當(dāng)施加給定頻率的電壓時電抗(或一組電抗)允許交流電流流動的容易程度。
電納與電抗符號相反所以電容電納 B C 為正值,(+ ve)為值,而電感電納 B L 為負(fù), (-ve)in value。
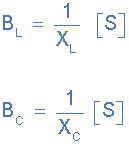
因此,我們可以將感應(yīng)和電容電納定義為:
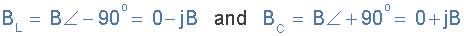
在AC串聯(lián)電路中,電流的阻抗是阻抗, Z 有兩個組件,電阻 R 和電抗, X ,從這兩個組件我們可以構(gòu)造一個阻抗三角形。類似地,在并聯(lián)RLC電路中,導(dǎo)納 Y 也有兩個分量,電導(dǎo), G 和電納, B 。這使得構(gòu)建導(dǎo)納三角形成為可能,其具有水平電導(dǎo)軸, G 和垂直電納軸 jB ,如圖所示。
并聯(lián)RLC電路的導(dǎo)納三角
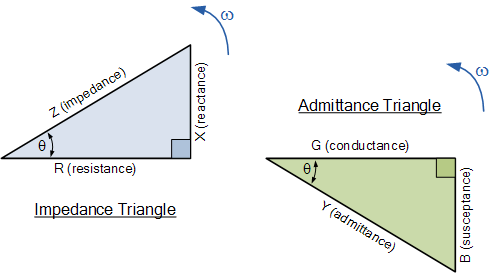
現(xiàn)在我們有一個導(dǎo)納三角形,我們可以使用畢達(dá)哥拉斯來計(jì)算所有三個邊的大小以及相位角,如圖所示。
來自畢達(dá)哥拉斯
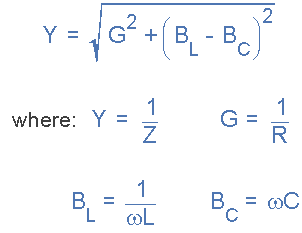
然后我們可以定義電路的導(dǎo)納和相對于導(dǎo)納的阻抗:
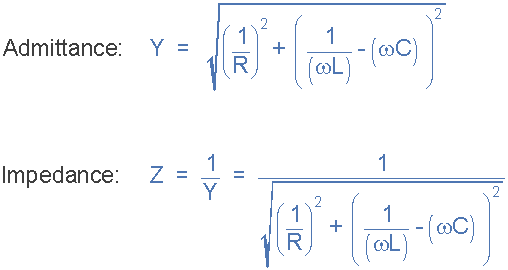
給我們一個功率因數(shù)角:
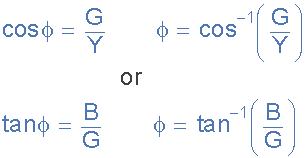
作為導(dǎo)納,并行RLC電路的 Y 是一個復(fù)雜的數(shù)量,對應(yīng)于串聯(lián)電路的阻抗 Z = R + jX 的一般形式的導(dǎo)納將寫為 Y = G - jB ,用于并聯(lián)電路,其中實(shí)部 G 是電導(dǎo),虛部 jB 是th e。電納。極性形式如下:
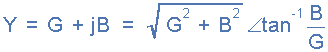
并聯(lián)RLC電路示例No1
A 1kΩ電阻, 142mH 線圈和 160uF 電容均通過240V,60Hz電源并聯(lián)。計(jì)算并聯(lián)RLC電路的阻抗和從電源汲取的電流。
并聯(lián)RLC電路的阻抗
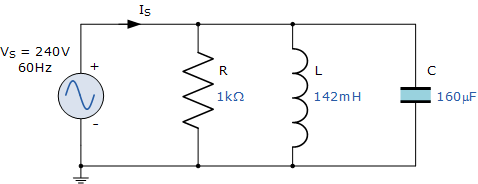
在交流電路中,電阻不受頻率的影響,因此 R =1kΩ
感應(yīng)電抗,( X L ):

電容電抗,( X C ):
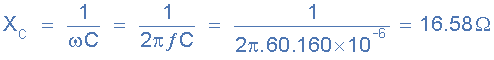
阻抗, ( Z ):
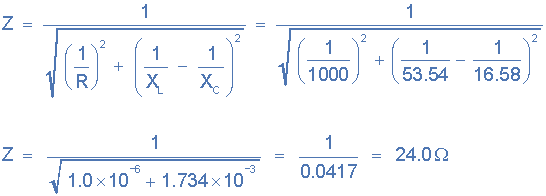
供應(yīng)電流,( ):
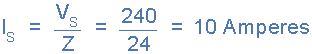
并聯(lián)RLC電路示例No2
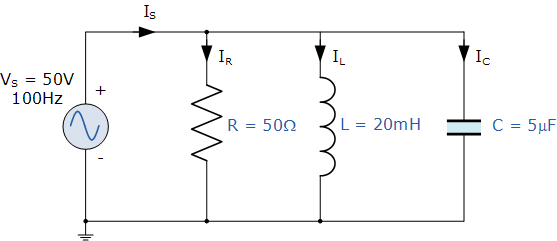
50Ω電阻, 20mH 線圈和 5uF 電容器均通過50V,100Hz電源并聯(lián)連接。計(jì)算從電源汲取的總電流,每個支路的電流,電路的總阻抗和相角。同時構(gòu)造代表電路的電流和導(dǎo)納三角形。
并聯(lián)RLC電路
1)。感應(yīng)電抗,( X L ):
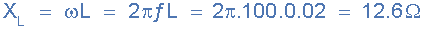
2)。電容電抗,( X C ):
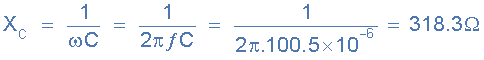
3)。阻抗,( Z ):
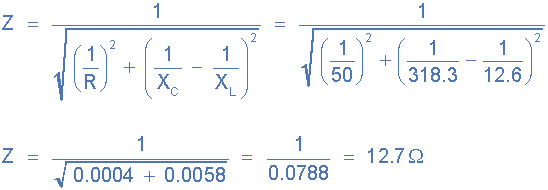
4)。電流通過電阻,R( I R ):
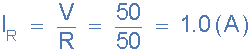
5)。通過電感的電流L( I L ):
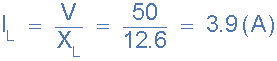
6)。電流通過電容C( I C ):

7)。總供電電流,( I S ):
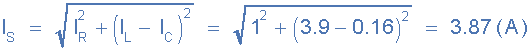
8)。電導(dǎo),( G ):
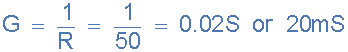
9)。感應(yīng)式電納,( B L ):
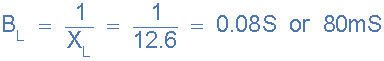
10)。電容電納,( B C ):
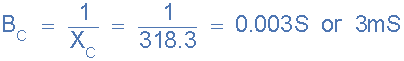
11)。準(zhǔn)入,( Y ):
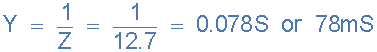
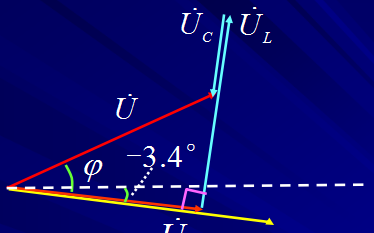
12)。合成電流和電源電壓之間的相角(φ):
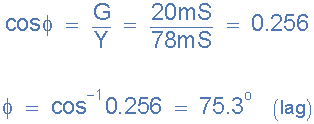
電流和導(dǎo)納三角形
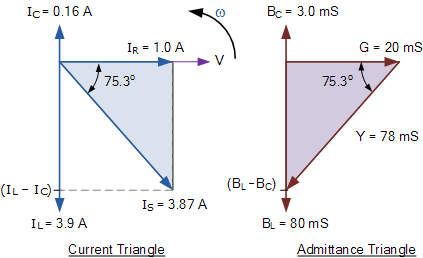
并聯(lián)RLC電路概述
在并聯(lián)RLC電路中包含電阻,電感和一個電容器,電路電流 I S 是由三個分量組成的相量和, I R , I L 和 I C ,所有三個電源電壓共用。由于電源電壓對所有三個元件都是通用的,因此在構(gòu)造電流三角形時,它可用作水平參考電壓。
可以使用與串聯(lián)RLC電路相同的矢量圖分析并行RLC網(wǎng)絡(luò)。然而,當(dāng)并聯(lián)RLC電路包含兩個或更多個電流分支時,對于并聯(lián)RLC電路的分析在數(shù)學(xué)上比對于串聯(lián)RLC電路更難。因此,可以使用稱為導(dǎo)納的阻抗的倒數(shù)來容易地分析AC并聯(lián)電路。
導(dǎo)納是給定符號 Y 的阻抗的倒數(shù)。與阻抗一樣,它是由實(shí)部和虛部組成的復(fù)數(shù)量。實(shí)部是電阻的倒數(shù),稱為電導(dǎo),符號 Y ,而虛部是電抗的倒數(shù),稱為電納,符號 B 并以復(fù)數(shù)形式表示為: Y = G + jB ,兩個復(fù)阻抗之間的對偶性定義為:
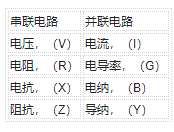
我們已經(jīng)看到了該串聯(lián)和并聯(lián)RLC電路在同一電路中包含容抗和電抗。如果我們改變這些電路的頻率,那么必須使容性電抗值等于感抗的頻率,因此 X C = X L .由于電納是電抗的倒數(shù),在感應(yīng)電路中,感應(yīng)電納, B L 的值為負(fù)值,在容性電路中,容性電納, B C 的值為正值。與 X L 和 X C 完全相反。
發(fā)生這種情況的頻率點(diǎn)稱為共振,在下一個教程中,我們將研究串聯(lián)諧振以及它的存在如何改變電路的特性。
-
電路
+關(guān)注
關(guān)注
173文章
6022瀏覽量
174560 -
電流
+關(guān)注
關(guān)注
40文章
7118瀏覽量
134338 -
阻抗
+關(guān)注
關(guān)注
17文章
970瀏覽量
47081 -
電壓
+關(guān)注
關(guān)注
45文章
5698瀏覽量
117358 -
并行
+關(guān)注
關(guān)注
0文章
80瀏覽量
19230
發(fā)布評論請先 登錄
技術(shù)干貨!一文讀懂電源技術(shù)之RLC電路分析
請教:RLC串聯(lián)電路的阻抗函數(shù)
射頻導(dǎo)納液位計(jì)及測量原理概述
電源技術(shù)之RLC電路分析(一)
電源技術(shù)之RLC電路分析(二)
電源技術(shù)之并聯(lián)諧振和RLC電路
RLC串聯(lián)電路的阻抗與電路頻率是成正比嗎?
基本元件并聯(lián)的交流電路與正弦交流電路的計(jì)算舉例
電源技術(shù)之RLC電路分析
幾種RLC并聯(lián)諧振電路特性的比較
正弦交流電路的阻抗、導(dǎo)納及等效轉(zhuǎn)換
阻抗和導(dǎo)納及正弦穩(wěn)態(tài)電路的分析和功率的概述
淺談PCBA設(shè)計(jì)的RLC電路并行設(shè)計(jì)
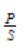





 并行RLC電路阻抗和導(dǎo)納定義案例概述分析
并行RLC電路阻抗和導(dǎo)納定義案例概述分析










評論