電氣工程中使用的數學將電阻,電流或直流電壓加在一起使用所謂的“實數”,用作整數或分數。
但實數不是我們需要使用的那種數字,特別是在處理頻率相關的正弦源和矢量時。除了使用正常數字或實數之外,還引入了復數,以便使用負數的平方根,√ 來解決復雜方程式。 1 。
在電氣工程中,這種類型的數字稱為“虛數”,為了區分虛數和實數,字母“ j ”已知通常在電氣工程中使用j-operator。因此,字母“ j ”放在實數前面以表示其虛數操作。
虛數的例子是: j3 , j12 , j100 等。然后復數由兩個不同但非常相關的部分組成,“實數”加上“虛數” “。
復數表示二維復數或s平面中以兩個不同軸為參照的點。水平軸稱為“實軸”,而垂直軸稱為“虛軸”。復數的實部和虛部分別縮寫為Re(z)和Im(z)。
由實數(有效成分)和虛數(無功成分)組成的復數)數字可以加上,減去和使用,與用基本代數分析直流電路完全相同。
數學中用于加減虛數的規則和定律與對于實數,j2 + j4 = j6等。唯一的區別在于乘法,因為兩個虛數相乘在一起變為負實數。實數也可以被認為是一個復數,但假想零部分標記為j0。
j-operator的值恰好等于√ -1 ,因此“ j ”,( jxj )的連續乘法將導致 j 具有以下值為 -1 , -j 和 +1 。由于j運算符通常用于指示向量的逆時針旋轉,因此每個連續的乘法或冪“ j ”, j 2 ,j 3 等將迫使矢量沿逆時針方向旋轉固定角度90° o ,如下所示。同樣,如果向量的乘法產生 -j 運算符,則相移將為-90 o ,即順時針旋轉。
矢量旋轉的j運算符
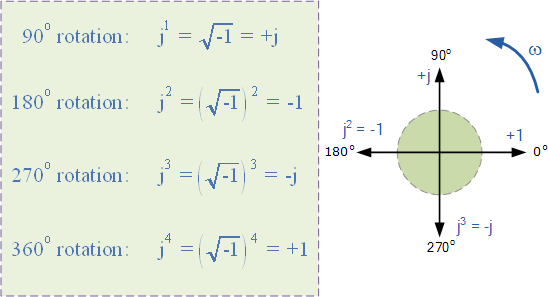
因此,通過將虛數乘以 j 2 將向量旋轉 180 o 逆時針旋轉,乘以 j 3 旋轉 270 o 并通過 j 4 將其旋轉 360 o 或回到原來的位置。乘以 j 10 或 j 30 將導致向量逆時針旋轉適當的量。在每次連續旋轉中,矢量的大小始終保持不變。
在電氣工程中,有不同的方式以圖形或數學方式表示復數。使用余弦和正弦規則的一種方法稱為笛卡爾或矩形形式。
使用矩形形式的復數
在關于Phasors的最后一個教程中,我們看到一個復數由一個實部和一個虛部表示,它采用通用形式:

其中:
Z - 是代表向量的復數
x - 是實部或活動部件
y - 是虛部或反應部件
j - 由√ -1
定義在矩形形式中,復數可以表示為二維點平面稱為復合或s-plane。因此,例如, Z = 6 + j4 表示單個點,其坐標在水平實軸上表示6,在垂直虛軸上表示4,如圖所示。
使用復數復雜或s面
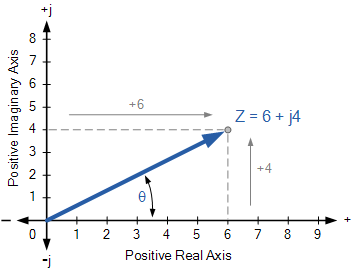
但是,由于矩形形式的復數的實部和虛部都可以是正數或負數,因此實軸和虛軸都必須同時擴展。正面和負面的方向。然后產生一個復雜的平面,有四個象限,稱為Argand Diagram,如下所示。
四象限Argand圖
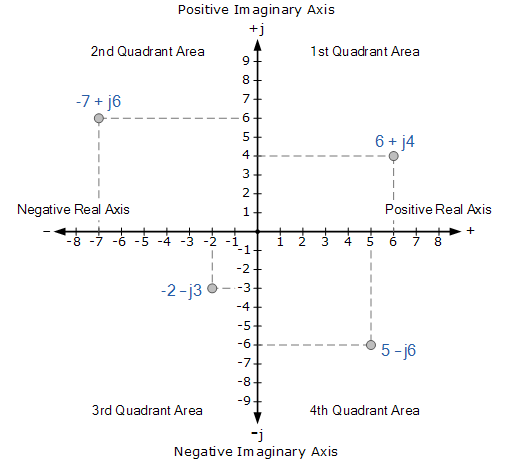
在Argand圖上,橫軸表示垂直虛軸右側的所有正實數,以及垂直虛軸左側的所有負實數。所有正虛數都表示在水平軸上方,而所有負虛數都低于水平實軸。然后生成一個二維復平面,其中有四個不同的象限,標記為 QI , QII , QIII 和 QIV 。
上面的Argand圖也可用于表示旋轉相量作為復平面中的一個點,其半徑由相量的大小給出,每個將圍繞它繪制一個完整的圓2π/ω秒。
然后我們可以進一步擴展這個想法,以顯示旋轉90° o 的極坐標和矩形形式的復數的定義。
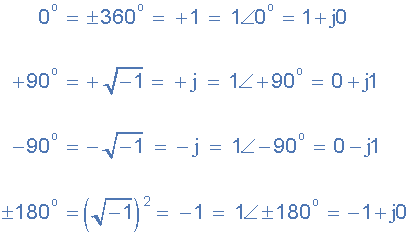
復數也可以有“零”實部或虛部等as: Z = 6 + j0 或 Z = 0 + j4 。在這種情況下,點直接繪制在實軸或虛軸上。此外,復數的角度可以使用簡單的三角法計算,以計算直角三角形的角度,或者從正實軸開始沿著Argand圖逆時針測量。
然后角度0和90 o 將位于第一象限( I ),角度(θ)介于90和180之間 o 在第二象限( II )。第三象限( III )包括180到270 o 之間的角度,而完成整個圓圈的第四個和最后一個象限( IV )包括270和360之間的角度 o 等。在所有四個象限中,相關角度可以從以下位置找到:
tan -1 (虛構成分÷實部成分)
復數的加法和減法
復數的加或減可以數學方式或以矩形形式進行圖形化。另外,實際部分首先加在一起形成和的實部,然后虛部形成和的虛部,這個過程如下使用兩個復數 A 和 B 作為示例。
復雜的加法和減法
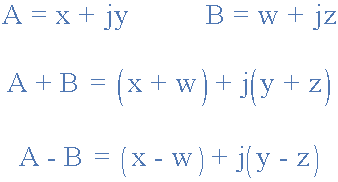
復數示例No1
兩個向量分別定義為 A = 4 + j1 和 B = 2 + j3 。確定矩形( a + jb )形式的兩個向量的和與差,并以圖形方式確定為Argand圖。
數學加法和減法
<跨度>加成
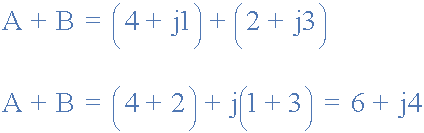
減法
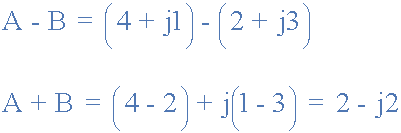
圖形添加和減法
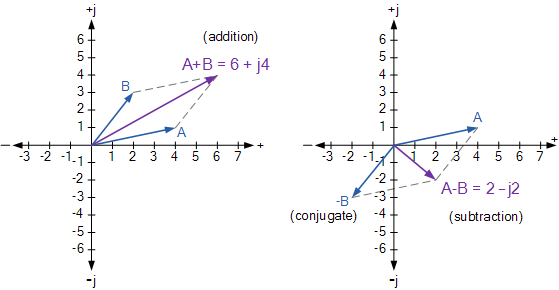
復數的乘法和除法
矩形形式中復數的乘法或多或少跟隨與正規代數相同的規則以及運算符的連續乘法的一些附加規則,其中: j 2 = - 1 。因此,例如,將 A = 4 + j1 和 B = 2 + j3 的兩個向量相乘,將得到以下結果。
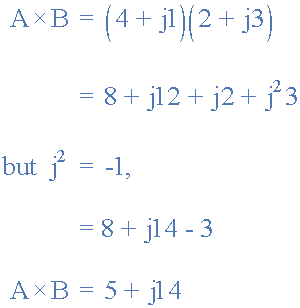
數學上,矩形復數的劃分有點難以執行,因為它需要使用分母共軛函數將等式的分母轉換為實數。這被稱為“合理化”。然后,復數的劃分最好使用“Polar Form”進行,我們將在后面介紹。但是,作為矩形形式的示例,我們可以找到vector A 的值除以vector B 。
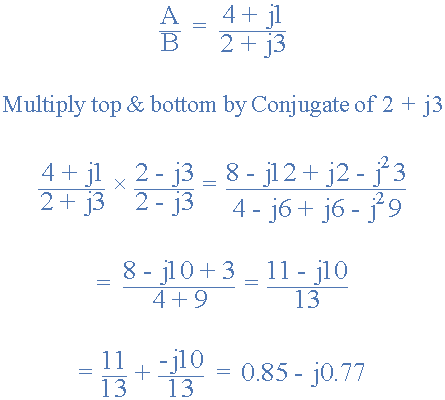
復共軛
復共軛,或簡單地共軛復數是通過反轉代數符號找到的復數虛數僅在保持實數的代數符號相同的同時識別 z的復共軛使用符號 z 。例如, z = 6 + j4 的共軛是 z = 6-j4 ,同樣 z = 6-的共軛j4 是 z = 6 + j4 。
復共軛的Argand圖上的點在水平位置上具有相同的水平位置。實軸作為原始復數,但垂直位置相反。因此,復共軛可以被認為是復數的反映。以下示例顯示復數, 6 + j4 及其在復平面中的共軛。
共軛復數
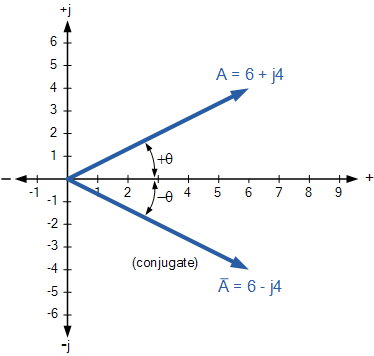
如上所述,復數與其復共軛的總和將始終為實數。然后,添加復數及其共軛僅將結果作為實數或有效分量,而它們的減法僅給出虛數或無功分量。復數的共軛是電氣工程中用于確定使用矩形形式的交流電路的視在功率的重要元素。
使用極坐標形式的復數
與矩形形式不同在復平面中繪制點,復數的極坐標是根據其大小和角度編寫的。因此,極坐標形式向量表示為: Z =A∠±θ,其中: Z 是極坐標形式的復數, A 是矢量的大小或模數,θ是 A 的角度或參數,可以是正數也可以是負數。該點的大小和角度仍然與上面的矩形形式相同,這次以極坐標形式表示點的位置以“三角形”表示,如下所示。
極性形式表示復數
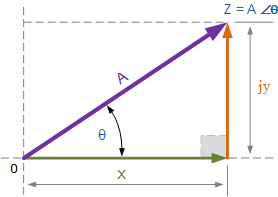
由于點的極坐標表示基于三角形,我們可以使用三角形的簡單幾何,尤其是三角形和畢達哥拉斯在三角形上的定理,以找出復數的大小和角度。正如我們從學校記得的那樣,三角學處理邊的關系和三角形的角度,因此我們可以將邊之間的關系描述為:
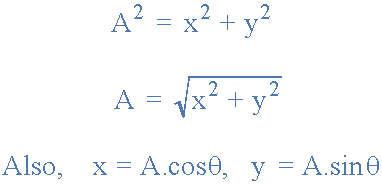
再次使用三角法,給出 A 的角度θ如下。

然后以Polar形式顯示 A 的長度及其角度表示復數而不是點。同樣以極性形式,復數的共軛具有相同的大小或模量,它是角度變化的符號,因此例如6∠30 o 將6∠-30 o 。
在矩形形式和極坐標形式之間轉換
在矩形形式中,我們可以根據其直角坐標表示矢量,水平軸是其實軸,垂直軸是其虛軸或j分量。在極坐標形式中,這些實軸和虛軸簡單地用“A∠θ”表示。然后使用上面的例子,矩形和極形之間的關系可以定義為。
將極性形式轉換為矩形,(P→R)
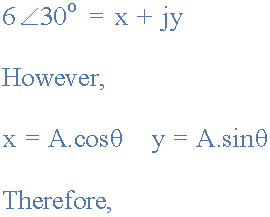
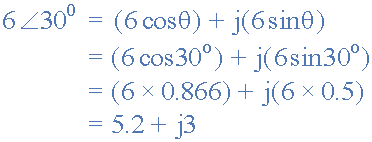
我們還可以將矩形轉換回極性形式,如下所示。
將矩形轉換為極坐標形式,(R→P)
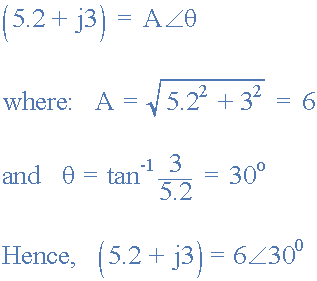
極地形式乘法和除法
矩形如上所述,形式最適合添加和減去復數,但極性形式通常更適合乘法和除法。為了將極坐標形式的兩個向量相乘,我們必須首先將兩個模數或大小相乘,然后將它們的角度加在一起。
極坐標中的乘法
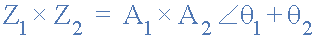
將6∠30 o 和8∠-45 o相乘 給我們。
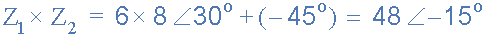
極地分裂
同樣,分開兩個極性形式的矢量,我們必須將兩個模數分開然后減去它們的角度,如圖所示。
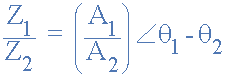
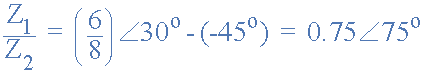
幸運的是,今天的現代科學計算器內置了數學函數(檢查你的書),允許輕松轉換矩形到極性形式( R→P ),然后從極性變為矩形,( R→P )。
使用指數形式的復數
到目前為止,我們已經考慮了矩形形式中的復數,( a + jb )和極地形式,(A∠±θ)。但是還有第三種表示復數的方法,該方法類似于對應于正弦曲線的長度(幅度)和相位角的極坐標形式,但使用自然對數的基數, e =2.718 281 .. 找到復數的值。第三種方法稱為指數形式。
指數形式使用正弦的三角函數( sin )和直角三角形的余弦( cos )值,將復指數定義為復平面中的旋轉點。尋找點位置的指數形式基于Euler's Identity,以瑞士數學家Leonhard Euler命名,并給出:
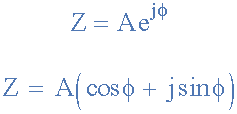
然后歐拉的身份可以用復平面上的以下旋轉相量圖表示。
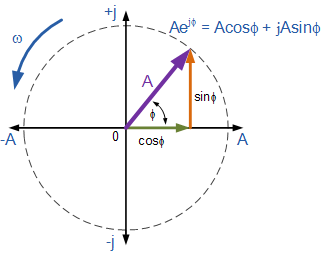
我們可以看到Euler的身份與上面的極性形式非常相似,并且它向我們顯示了一個數字,例如 A e jθ 幅度為1的>也是一個復數。我們不僅可以將指數形式的復數轉換為極性形式,例如: 2 e j30 =2∠30, 10 j120 =10∠120或 -6 j90 = - 6∠90,但歐拉的身份也為我們提供了一種將復數從指數形式轉換為矩形形式的方法。然后,在定義復數時,指數,極坐標和矩形之間的關系給出為。
復數形式
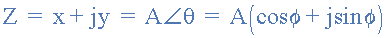
相量符號
到目前為止,我們已經看到了表示旋轉的不同方式矢量或固定矢量使用復數來定義復雜平面上的點。相量符號是構造具有給定正弦波形的幅度和相位角的單個復數的過程。
然后相量符號或相量變換,因為它有時被稱為,傳遞真實部分正弦函數: A (t) = A m cos(ωt±Φ)從時域到復數域,也被稱為頻域。例如:
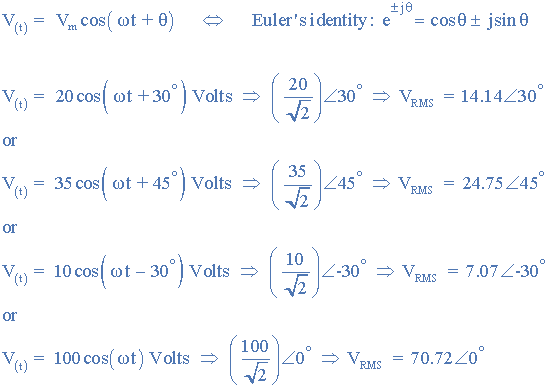
請注意√ 2 將最大振幅轉換為a <有效或RMS值,相位角以弧度表示,(ω)。
復數匯總
然后總結本教程關于復雜數字以及在電氣工程中使用復數。
復數由兩個不同的數字組成,一個實數加上一個虛數。
虛數通過使用j與實數區分開來-operator。
前面帶有字母“ j ”的數字將其標識為復合體中的虛數平面。
根據定義,j-operator j≡√ -1
可以添加,減去,乘以虛數
“ j ”乘以“ j “給出 j 2 = - 1
在矩形表格中,復數表示為復雜平面上的空間點。
在Polar Form中,復數由一條線表示,其長度為幅度和相位角。 / li>
在指數形式中,復數由一條線和相應的角度表示,該角度使用自然對數的底數。
復數可以用以下三種方式之一表示:
Z = x + jy ?矩形表格
Z =A∠Φ?極地形式
Z = A jΦ ?指數形式
Euler的身份可用于轉換復雜從指數形式到矩形的數字。
在前面的教程中,我們已經看到我們可以使用相量來表示正弦波形,并且它們的幅度和相位角可以寫在形式復雜的數字。我們還看到復數可以以矩形,極坐標或指數形式呈現,每個復數代數形式之間的轉換包括加法,減法,乘法和除法。
在接下來的幾個與AC串聯電路中的相量關系相關的教程中,我們將研究一些常見無源電路元件的阻抗,并繪制流過元件的電流和施加在其上的電壓的相量圖。交流阻力。
-
運算
+關注
關注
0文章
132瀏覽量
26164 -
計算器
+關注
關注
16文章
439瀏覽量
38005 -
相量
+關注
關注
0文章
6瀏覽量
7944
發布評論請先 登錄





 復數和相量運算復數定義及案例轉換匯總
復數和相量運算復數定義及案例轉換匯總












評論